Теорема 7.23. Коэффициент характеристического уравнения при  равен
равен  .
.
Доказательство получается раскрытием определителя  .
.
Сумма элементов матрицы A, расположенных на главной диагонали, называется следом матрицы. След матрицы является коэффициентом характеристического многочлена и не зависит от выбора базиса..
7.7 Диагонализируемые преобразования
Линейное преобразование называется диагонализируемым, если существует базис, в котором матрица линейного преобразования имеет диагональный вид. Заметим, что базис, в котором матрица линейного преобразования имеет диагональный вид, образован собственными векторами. Верно и обратное. В базисе из собственных векторов матрица линейного преобразования имеет диагональный вид. Не каждое линейное преобразование диагонализируемо. Например, линейное преобразование, заданное матрицей  не диагонализируемо.
не диагонализируемо.
Теорема 7.24. Собственные векторы, отвечающие различным собственным значениям, линейно независимы.
Доказательство. Пусть  - линейно независимая система собственных векторов, соответствующих собственному значению
- линейно независимая система собственных векторов, соответствующих собственному значению 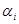 , где i =1,…, s. Покажем линейную независимость системы векторов
, где i =1,…, s. Покажем линейную независимость системы векторов  индукцией по s. При s =1 утверждение очевидно. Пусть оно верно для s -1. Покажем его справедливость для s. Допустим, система
индукцией по s. При s =1 утверждение очевидно. Пусть оно верно для s -1. Покажем его справедливость для s. Допустим, система  - линейно зависима. Тогда найдутся коэффициенты
- линейно зависима. Тогда найдутся коэффициенты  не все равные нулю, что
не все равные нулю, что  . Из этого равенства выводим
. Из этого равенства выводим  или
или  . По предположению индукции все коэффициенты в этом равенстве равны 0, и, значит
. По предположению индукции все коэффициенты в этом равенстве равны 0, и, значит 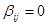 при i < s. Но тогда система
при i < s. Но тогда система  - линейно зависима, что противоречит условиям теоремы. К полученному противоречию привело допущение о линейной зависимости системы векторов
- линейно зависима, что противоречит условиям теоремы. К полученному противоречию привело допущение о линейной зависимости системы векторов  , значит, эта система линейно независима, что и требовалось доказать.
, значит, эта система линейно независима, что и требовалось доказать.
Рассмотрим вопрос о количестве линейно независимых собственных векторов, соответствующих собственному числу  .
.
Геометрической кратностью собственного числа  называется дефект преобразования
называется дефект преобразования 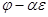 , а алгебраической кратностью называется кратность корня
, а алгебраической кратностью называется кратность корня  в характеристическом многочлене.
в характеристическом многочлене.
Теорема 7.25. Геометрическая кратность  не превосходит его алгебраической кратности.
не превосходит его алгебраической кратности.
Доказательство. Пусть геометрическая кратность  равна k. Дополним базис
равна k. Дополним базис  ядра преобразования
ядра преобразования 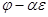 до базиса всего пространства
до базиса всего пространства  . Матрица линейного преобразования в этом базисе имеет вид
. Матрица линейного преобразования в этом базисе имеет вид  и характеристический многочлен равен
и характеристический многочлен равен  . Таким образом, алгебраическая кратность
. Таким образом, алгебраическая кратность  не меньше геометрической кратности, что и требовалось доказать.
не меньше геометрической кратности, что и требовалось доказать.
Теорема 7.26 Линейное преобразование  линейного пространства V над числовым полем P диагонализируемо тогда и только тогда, когда характеристический многочлен раскладывается над полем P на линейные множители и алгебраическая кратность каждого корня совпадает с его геометрической кратностью.
линейного пространства V над числовым полем P диагонализируемо тогда и только тогда, когда характеристический многочлен раскладывается над полем P на линейные множители и алгебраическая кратность каждого корня совпадает с его геометрической кратностью.
Доказательство очевидно.
Теорема Шура
Пусть  - линейное преобразование пространства V над полем комплексных чисел C. Линейное преобразование
- линейное преобразование пространства V над полем комплексных чисел C. Линейное преобразование  имеет хотя бы один собственный вектор (Следствие 7.16). Этот факт можно усилить.
имеет хотя бы один собственный вектор (Следствие 7.16). Этот факт можно усилить.
Теорема 7.27. Пусть  - линейное преобразование пространства V над полем комплексных чисел C. Существует базис V, в котором матрица линейного преобразования
- линейное преобразование пространства V над полем комплексных чисел C. Существует базис V, в котором матрица линейного преобразования  имеет верхний треугольный вид.
имеет верхний треугольный вид.
Доказательство проведем индукцией по размерности V. Пусть утверждение верно для линейных преобразований (n -1)-мерных пространств. Покажем его справедливость для линейного преобразования  n -мерного линейного пространства V. Поскольку линейное пространство над полем C, то существует собственный вектор h этого линейного преобразования. Дополним этот вектор до базиса всего пространства векторами
n -мерного линейного пространства V. Поскольку линейное пространство над полем C, то существует собственный вектор h этого линейного преобразования. Дополним этот вектор до базиса всего пространства векторами 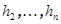 . Матрица линейного преобразования в этом базисе имеет блочный вид
. Матрица линейного преобразования в этом базисе имеет блочный вид  , где
, где  - собственное число для вектора h. Обозначим через W линейную оболочку векторов
- собственное число для вектора h. Обозначим через W линейную оболочку векторов 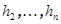 . Векторы
. Векторы 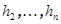 образуют базис W. Обозначим через
образуют базис W. Обозначим через 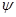 линейное преобразование W, матрица которого в базисе
линейное преобразование W, матрица которого в базисе 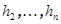 равна A. По предположению индукции в подпространстве W существует базис
равна A. По предположению индукции в подпространстве W существует базис 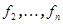 , в котором матрица линейного преобразования имеет верхний треугольный вид. Пусть T – матрица перехода к этому базису. Тогда
, в котором матрица линейного преобразования имеет верхний треугольный вид. Пусть T – матрица перехода к этому базису. Тогда  - верхняя треугольная матрица. Матрица перехода от базиса
- верхняя треугольная матрица. Матрица перехода от базиса 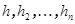 к базису
к базису 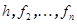 равна
равна 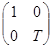 , и, значит, матрица
, и, значит, матрица  в базисе
в базисе  равна
равна  , то есть является верхней треугольной.
, то есть является верхней треугольной.
Аналогом доказанной теоремы над полем вещественных чисел является следующий результат.
Теорема 7.28. Пусть  - линейное преобразование пространства V над полем вещественных чисел R. Существует базис V, в котором матрица линейного преобразования
- линейное преобразование пространства V над полем вещественных чисел R. Существует базис V, в котором матрица линейного преобразования  имеет блочный верхний треугольный вид. По главной диагонали стоят блоки первого и второго порядка.
имеет блочный верхний треугольный вид. По главной диагонали стоят блоки первого и второго порядка.
Доказательство проведем индукцией по размерности n пространства V. Пусть утверждение верно для линейных преобразований пространств размерности меньшей n. Покажем его справедливость для линейного преобразования  n -мерного линейного пространства V. Линейное преобразование
n -мерного линейного пространства V. Линейное преобразование  имеет либо одномерное, либо двумерное инвариантное подпространство (Следствие 7.17). Дополним базис этого инвариантного подпространства до базиса всего пространства векторами
имеет либо одномерное, либо двумерное инвариантное подпространство (Следствие 7.17). Дополним базис этого инвариантного подпространства до базиса всего пространства векторами  , где k равно либо 2, либо 3. Матрица линейного преобразования в этом базисе имеет блочный вид
, где k равно либо 2, либо 3. Матрица линейного преобразования в этом базисе имеет блочный вид  , где
, где  - блок либо первого, либо второго порядка. Далее, рассуждения повторяют доказательство теоремы 7.6.
- блок либо первого, либо второго порядка. Далее, рассуждения повторяют доказательство теоремы 7.6.
Теорема 7.29. (теорема Шура). Для линейного преобразования  унитарного пространства V существует ортонормированный базис, в котором матрица линейного преобразования
унитарного пространства V существует ортонормированный базис, в котором матрица линейного преобразования  имеет верхний треугольный вид.
имеет верхний треугольный вид.
Доказательство. Пусть  - базис V, в котором матрица линейного преобразования
- базис V, в котором матрица линейного преобразования  имеет верхний треугольный вид (Теорема 7.27). Применим к базису процесс ортогонализации и построим ортогональный базис
имеет верхний треугольный вид (Теорема 7.27). Применим к базису процесс ортогонализации и построим ортогональный базис 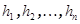 . Матрица перехода T от базиса
. Матрица перехода T от базиса 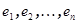 к базису
к базису 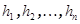 - верхняя треугольная и
- верхняя треугольная и 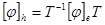 . Поскольку произведение верхних треугольных матриц является верхней треугольной матрицей, то матрица
. Поскольку произведение верхних треугольных матриц является верхней треугольной матрицей, то матрица  - верхняя треугольная. Положим
- верхняя треугольная. Положим 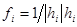 , где i= 1,…, n. Базис
, где i= 1,…, n. Базис 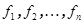 - ортонормированный и матрица линейного преобразования в этом базисе – верхняя треугольная, тем самым теорема доказана.
- ортонормированный и матрица линейного преобразования в этом базисе – верхняя треугольная, тем самым теорема доказана.
Теорема 7.30. Для линейного преобразования  евклидова пространства V существует ортонормированный базис, в котором матрица линейного преобразования
евклидова пространства V существует ортонормированный базис, в котором матрица линейного преобразования  имеет блочный верхний треугольный вид. По главной диагонали расположены блоки первого и второго порядков.
имеет блочный верхний треугольный вид. По главной диагонали расположены блоки первого и второго порядков.
Доказательство аналогично доказательству теоремы 7.7.
8 Сопряженные преобразования.
8.1 Линейное преобразование и билинейные функции
Пусть V евклидово (унитарное) пространство. Обозначим через 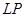 множество всех линейных преобразований пространства V, а через B множество билинейных функций, заданных на V. Если
множество всех линейных преобразований пространства V, а через B множество билинейных функций, заданных на V. Если  , то функция
, то функция 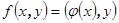 является билинейной. Таким образом, определено однозначное отображение множества линейных преобразований LP в множество билинейных функций B. Исследуем свойства этого отображения.
является билинейной. Таким образом, определено однозначное отображение множества линейных преобразований LP в множество билинейных функций B. Исследуем свойства этого отображения.
Свойство 8.19. Разные линейные преобразования отображаются в разные билинейные функции.
Доказательство проведем методом от противного. Пусть найдутся два разных линейных преобразования  и
и 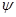 , которые отображаются в одну и ту же билинейную функцию. Тогда для любых векторов
, которые отображаются в одну и ту же билинейную функцию. Тогда для любых векторов 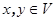 справедливо равенство
справедливо равенство 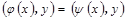 или
или  . Положим
. Положим 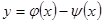 , тогда
, тогда  и
и 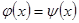 для любого вектора
для любого вектора 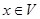 . Это означат, что линейные преобразования равны, что противоречит допущению.
. Это означат, что линейные преобразования равны, что противоречит допущению.
Свойство 8.20. Отображение линейных преобразований в билинейные функции взаимно однозначно.
Доказательство. Покажем, что для любой билинейной функции 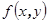 существует линейное преобразование
существует линейное преобразование  , что
, что 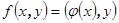 . Для каждого вектора x определим подпространство
. Для каждого вектора x определим подпространство 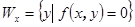 . Ортогональное дополнение к этому подпространству имеет размерность не выше 1. Действительно, если
. Ортогональное дополнение к этому подпространству имеет размерность не выше 1. Действительно, если 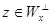 и
и  , то
, то 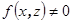 и для вектора
и для вектора  справедливо включение
справедливо включение 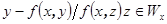 , и, значит
, и, значит  . Определим функцию
. Определим функцию 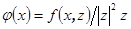 , где z – базис
, где z – базис 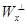 . Если
. Если 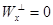 , то положим
, то положим 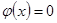 . Легко убедиться, что
. Легко убедиться, что  , и, значит функция
, и, значит функция  - линейное преобразование.
- линейное преобразование.
Аналогично, можно рассмотреть отображение LP на B, задаваемое формулой  . Это отображение взаимно однозначно.
. Это отображение взаимно однозначно.
Линейное преобразование 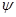 называется сопряженным преобразованием к
называется сопряженным преобразованием к  , если для любых векторов x,y из V справедливо равенство
, если для любых векторов x,y из V справедливо равенство 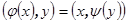 . Сопряженное преобразование к
. Сопряженное преобразование к  обозначают
обозначают 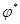 .
.
8.2 Сопряженное преобразование. Свойства.
Пусть e1,…,en базис V,  - матрица линейного преобразования
- матрица линейного преобразования  , G e – матрица Грама скалярного произведения. Перейдем от равенства векторов
, G e – матрица Грама скалярного произведения. Перейдем от равенства векторов 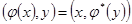 к равенству координат
к равенству координат 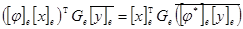 . Из этого равенства выводим
. Из этого равенства выводим  . В случае ортонормированного базиса формула принимает более простой вид
. В случае ортонормированного базиса формула принимает более простой вид 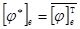 . Для евклидова пространства, знак комплексного сопряжения можно опустить.
. Для евклидова пространства, знак комплексного сопряжения можно опустить.
Свойство 8.21. Перечислим свойства сопряженного преобразования
1) 
2) 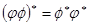
3) 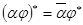
4) 
5) Если W инвариантное подпространство  , то ортогональное дополнение к W инвариантно относительно
, то ортогональное дополнение к W инвариантно относительно 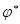 .
.
Доказательство. Из равенства  выводим первое свойство. Второе свойство получается из равенств
выводим первое свойство. Второе свойство получается из равенств  . Для доказательства третьего свойства достаточно рассмотреть равенства
. Для доказательства третьего свойства достаточно рассмотреть равенства 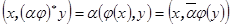 . Четвертое свойство доказывается равенствами
. Четвертое свойство доказывается равенствами  . Докажем пятое свойство. Для произвольного вектора x из W и произвольного вектора
. Докажем пятое свойство. Для произвольного вектора x из W и произвольного вектора 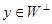 скалярное произведение
скалярное произведение  . По определению сопряженного преобразования
. По определению сопряженного преобразования 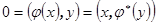 , и, значит
, и, значит  , что и требовалось доказать.
, что и требовалось доказать.
Пятое свойство позволяет дать другое доказательство теоремы Шура.
8.3 Нормальное преобразование и его свойства.
Преобразование называется нормальным, если оно перестановочно с сопряженным преобразованием, то есть 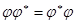 .
.
Свойство 8.22. Если x собственный вектор нормального преобразования  с собственным значением
с собственным значением  , то x собственный вектор
, то x собственный вектор 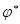 с собственным значением
с собственным значением  .
.
Доказательство. Пусть  . Поскольку
. Поскольку 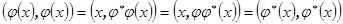 и
и 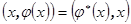 , то
, то 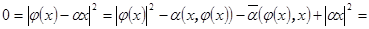
 .
.
Свойство 8.23. Собственные векторы нормального преобразования, соответствующие разным собственным значениям ортогональны.
Доказательство. Пусть x и y – собственные векторы нормального преобразования  , соответствующие разным собственным значениям
, соответствующие разным собственным значениям  и
и  (
( ,
, 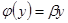 ). Из равенств
). Из равенств 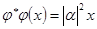 и
и 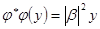 (Свойство 8.22) выводим
(Свойство 8.22) выводим  ,
, 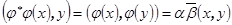 ,
, 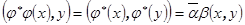 ,
,  . Далее,
. Далее,  , откуда
, откуда 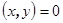 .
.
Теорема 8.31. Для нормального преобразования конечномерного унитарного пространства существует ортонормированный базис из собственных векторов.
Доказательство. Путь  - ортонормированный базис унитарного пространства V, в котором матрица нормального преобразования
- ортонормированный базис унитарного пространства V, в котором матрица нормального преобразования  является верхней треугольной. Пусть
является верхней треугольной. Пусть  , тогда
, тогда 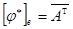 . Из равенства
. Из равенства  вытекает, что матрица A – диагональная, и, значит, базис
вытекает, что матрица A – диагональная, и, значит, базис  составлен из собственных векторов.
составлен из собственных векторов.
Построение ортонормированного базиса из собственных векторов, в котором матрица нормального преобразования диагонализируема, можно осуществлять следующим образом. Найти какой ни будь базис из собственных векторов. При этом, собственные векторы, соответствующие разным собственным числам заведомо ортогональны (Свойство 8.23). Условие ортогональности может нарушаться только на собственных векторах, соответствующих одному и тому же собственному значению.
Если матрица линейного преобразования диагонализируема, то всегда можно ввести скалярное произведение таким образом, чтобы линейное преобразование стало нормальным.
Теорема 8.32. Для нормального преобразования конечномерного евклидова пространства существует ортонормированный базис, в котором матрица линейного преобразования имеет блочно-диагональный вид. По главной диагонали расположены блоки первого и второго порядка.
Доказательство. Путь  - ортонормированный базис евклидова пространства V, в котором матрица нормального преобразования
- ортонормированный базис евклидова пространства V, в котором матрица нормального преобразования  является блочной верхней треугольной. Пусть
является блочной верхней треугольной. Пусть  , тогда
, тогда  . Из равенства
. Из равенства 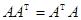 вытекает, что матрица A – блочно диагональная, что и требовалось доказать.
вытекает, что матрица A – блочно диагональная, что и требовалось доказать.
К сожалению, приведенное доказательство не раскрывает структуру блоков второго порядка, расположенных на главной диагонали. Поэтому дадим другое доказательство этой теоремы.
Доказательство 2. Множество  является линейным пространством над полем комплексных чисел C. В этом линейном пространстве введем скалярное произведение
является линейным пространством над полем комплексных чисел C. В этом линейном пространстве введем скалярное произведение  . Определим линейное преобразование пространства
. Определим линейное преобразование пространства  как
как  . Пусть
. Пусть  - ортонормированный базис
- ортонормированный базис  , тогда
, тогда  - ортонормированный базис унитарного пространства
- ортонормированный базис унитарного пространства  и
и 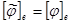 - матрица с вещественными элементами. Далее,
- матрица с вещественными элементами. Далее,  ,
,  и из равенства матриц
и из равенства матриц 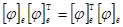 выводим равенство
выводим равенство  , то есть преобразование
, то есть преобразование 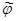 - нормальное. Следовательно, существует ортонормированный базис
- нормальное. Следовательно, существует ортонормированный базис 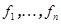 унитарного пространства
унитарного пространства  из собственных векторов нормального преобразования
из собственных векторов нормального преобразования 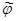 . Пусть
. Пусть  - собственные числа этих векторов. Заметим, что ортонормированный базис
- собственные числа этих векторов. Заметим, что ортонормированный базис  получается объединением ортонормированных базисов подпространств
получается объединением ортонормированных базисов подпространств  . Если собственное число
. Если собственное число  вещественное, то ортонормированный базис подпространства
вещественное, то ортонормированный базис подпространства  является также ортонормированным базисом подпространства
является также ортонормированным базисом подпространства  . Поэтому, не нарушая общности можно считать, что вещественным собственным числам в базисе
. Поэтому, не нарушая общности можно считать, что вещественным собственным числам в базисе 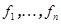 соответствуют векторы из V. Пусть f = x + iy – собственный вектор
соответствуют векторы из V. Пусть f = x + iy – собственный вектор 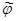 с комплексным собственным числом
с комплексным собственным числом 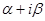 , тогда из равенств
, тогда из равенств  и
и  выводим
выводим  ,
,  , то есть линейное подпространство, натянутое на векторы x, y – инвариантно. Из полученных равенств вытекает
, то есть линейное подпространство, натянутое на векторы x, y – инвариантно. Из полученных равенств вытекает  , то есть вектор x - iy – собственный с собственным числом
, то есть вектор x - iy – собственный с собственным числом  . Если
. Если  ортонормированный базис
ортонормированный базис  , то
, то 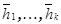 - ортонормированный базис
- ортонормированный базис  , поэтому, можно считать, что в базисе
, поэтому, можно считать, что в базисе 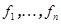 собственные векторы с комплексными собственными числами разбиты на пары. Рассмотрим пару
собственные векторы с комплексными собственными числами разбиты на пары. Рассмотрим пару  ,
,  собственных векторов с собственными числами
собственных векторов с собственными числами 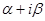 и
и  . Эти векторы ортогональны всем остальным векторам из базиса, следовательно, векторы
. Эти векторы ортогональны всем остальным векторам из базиса, следовательно, векторы  ортогональны всем остальным векторам. Далее,
ортогональны всем остальным векторам. Далее, 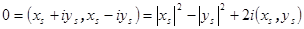 , откуда выводим
, откуда выводим  и
и  . Заменим векторы
. Заменим векторы  и
и  на
на 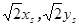 получим ортонормированный базис пространства V, в котором матрица линейного преобразования имеет блочно диагональный вид. По главной диагонали расположены блоки первого порядка, отвечающие вещественным собственным значениям, и блоки второго порядка
получим ортонормированный базис пространства V, в котором матрица линейного преобразования имеет блочно диагональный вид. По главной диагонали расположены блоки первого порядка, отвечающие вещественным собственным значениям, и блоки второго порядка  , отвечающие
, отвечающие 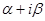 комплексным собственным значениям.
комплексным собственным значениям.
Если матрица линейного преобразования диагонализируема, то всегда можно ввести скалярное произведение таким образом, чтобы линейное преобразование стало нормальным.
8.4 Ортогональные преобразования
Линейное преобразование называется ортогональным (унитарным) если оно сохраняет скалярное произведение, то есть  . Из определения выводим
. Из определения выводим  или
или  . Таким образом ортогональное преобразование является нормальным.
. Таким образом ортогональное преобразование является нормальным.
Свойство 8.24. Собственные числа ортогонального преобразования по модулю равны 1.
Доказательство. Пусть  , тогда
, тогда  , и, значит,
, и, значит,  .
.
Следствие 8.18. Ортогональное преобразование евклидова пространства, в некотором ортонормированном базисе, сводится к выполнению последовательности тождественных преобразований, симметрий и поворотов в координатных плоскостях.
Доказательство. Ортогональное преобразование нормально, следовательно, существует ортонормированный базис, в котором матрица линейного преобразования имеет блочно диагональный вид. Блоки первого порядка соответствуют вещественным собственным числам, а блоки второго порядка – комплексным числам. Так как собственные числа ортогонального преобразования по модулю равны 1, то по главной диагонали могут стоять либо 1, либо -1, либо блок второго порядка  . Для доказательства осталось заметить, что геометрический смысл указанных преобразований как раз и есть тождественные преобразования, симметрии и повороты в координатных плоскостях.
. Для доказательства осталось заметить, что геометрический смысл указанных преобразований как раз и есть тождественные преобразования, симметрии и повороты в координатных плоскостях.
8.5 Самосопряженное преобразование.
Линейное преобразование называется самосопряженным, если  .
.
Свойство 8.25. Собственные числа самосопряженного преобразования – вещественны.
Доказательство. Пусть x –собственный вектор самосопряженного преобразования  (т.е.
(т.е.  ). Из равенств
). Из равенств  выводим
выводим 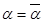 , то есть
, то есть  .
.
Следствие 8.19. Для самосопряженного линейного преобразования евклидова пространства существует ортонормированный базис из собственных векторов.
Доказательство. Самосопряженное преобразование является нормальным, и значит, существует ортонормированный базис, в котором матрица линейного преобразования имеет блочно диагональный вид. Поскольку все собственные числа вещественные, то все блоки первого порядка.
Полярное разложение
Самосопряженное преобразование  называется положительно определенным, если
называется положительно определенным, если  .
.
Следствие 8.20. Все собственные числа положительно определенного самосопряженного линейного преобразования неотрицательны.
Доказательство. Пусть  , тогда
, тогда  , и, значит,
, и, значит,  .
.
Теорема 8.33. (извлечение корня) Для положительно определенного самосопряженного линейного преобразования  существует единственное положительно определенное самосопряженное преобразование
существует единственное положительно определенное самосопряженное преобразование 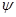 , что
, что  .
.
Доказательство. Пусть  - ортонормированный базис линейного пространства, в котором матрица
- ортонормированный базис линейного пространства, в котором матрица  - диагональная. Пусть
- диагональная. Пусть 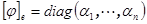 . Все числа стоящие на главной диагонали неотрицательны. Положим
. Все числа стоящие на главной диагонали неотрицательны. Положим  . Легко убедиться, что линейное преобразование
. Легко убедиться, что линейное преобразование 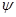 является положительно определенным самосопряженным преобразованием и
является положительно определенным самосопряженным преобразованием и  . Единственность очевидна.
. Единственность очевидна.
Теорема 8.34 (полярное разложение) Любое линейное преобразование  можно представить в виде произведения самосопряженного положительно определенного линейного преобразования
можно представить в виде произведения самосопряженного положительно определенного линейного преобразования 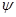 и ортогонального преобразования
и ортогонального преобразования  . Если
. Если  - невырожденное, то представление единственно. Разложение
- невырожденное, то представление единственно. Разложение  называется правым, а разложение
называется правым, а разложение  - левым.
- левым.
Доказательство. Преобразование  является самосопряженным и положительно определенным. Построим ортонормированный базис
является самосопряженным и положительно определенным. Построим ортонормированный базис  преобразования
преобразования  , при этом расположим собственные векторы, соответствующие нулевому собственному значению в конце базиса. Пусть
, при этом расположим собственные векторы, соответствующие нулевому собственному значению в конце базиса. Пусть  - собственные векторы с не нулевыми собственными значениями, а
- собственные векторы с не нулевыми собственными значениями, а  - собственные векторы с нулевым собственным значением. Матрица
- собственные векторы с нулевым собственным значением. Матрица  - диагональная, поэтому первые k строк матрицы
- диагональная, поэтому первые k строк матрицы 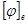 образуют ортогональную систему, а остальные равны 0. Длина j строки равна
образуют ортогональную систему, а остальные равны 0. Длина j строки равна  . Обозначим через
. Обозначим через  первые k строк матрицы
первые k строк матрицы 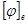 и дополним ортонормированную систему векторов
и дополним ортонормированную систему векторов  векторами
векторами  до ортонормированного базиса всего пространства. Обозначим через
до ортонормированного базиса всего пространства. Обозначим через  ортогональное преобразование, матрица которого в базисе
ортогональное преобразование, матрица которого в базисе  образована строками
образована строками  , а через
, а через 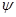 - положительно определенное самосопряженное преобразование, матрица которого в базисе
- положительно определенное самосопряженное преобразование, матрица которого в базисе  диагональная и равна
диагональная и равна  . Легко убедиться, что
. Легко убедиться, что  .
.
Для построения левого разложения достаточно найти правое разложение для сопряженного преобразования.
Поскольку  , то преобразование
, то преобразование 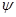 определяется единственным образом. Если преобразование
определяется единственным образом. Если преобразование  - невырожденное, то преобразование
- невырожденное, то преобразование 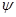 невырожденное, и, значит,
невырожденное, и, значит,  определяется единственным образом.
определяется единственным образом.


 равен
равен  .
. .
. не диагонализируемо.
не диагонализируемо. - линейно независимая система собственных векторов, соответствующих собственному значению
- линейно независимая система собственных векторов, соответствующих собственному значению 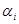 , где i =1,…, s. Покажем линейную независимость системы векторов
, где i =1,…, s. Покажем линейную независимость системы векторов  индукцией по s. При s =1 утверждение очевидно. Пусть оно верно для s -1. Покажем его справедливость для s. Допустим, система
индукцией по s. При s =1 утверждение очевидно. Пусть оно верно для s -1. Покажем его справедливость для s. Допустим, система  не все равные нулю, что
не все равные нулю, что  . Из этого равенства выводим
. Из этого равенства выводим  или
или  . По предположению индукции все коэффициенты в этом равенстве равны 0, и, значит
. По предположению индукции все коэффициенты в этом равенстве равны 0, и, значит 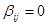 при i < s. Но тогда система
при i < s. Но тогда система  - линейно зависима, что противоречит условиям теоремы. К полученному противоречию привело допущение о линейной зависимости системы векторов
- линейно зависима, что противоречит условиям теоремы. К полученному противоречию привело допущение о линейной зависимости системы векторов  .
.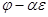 , а алгебраической кратностью называется кратность корня
, а алгебраической кратностью называется кратность корня  ядра преобразования
ядра преобразования  . Матрица линейного преобразования в этом базисе имеет вид
. Матрица линейного преобразования в этом базисе имеет вид  и характеристический многочлен равен
и характеристический многочлен равен  . Таким образом, алгебраическая кратность
. Таким образом, алгебраическая кратность  линейного пространства V над числовым полем P диагонализируемо тогда и только тогда, когда характеристический многочлен раскладывается над полем P на линейные множители и алгебраическая кратность каждого корня совпадает с его геометрической кратностью.
линейного пространства V над числовым полем P диагонализируемо тогда и только тогда, когда характеристический многочлен раскладывается над полем P на линейные множители и алгебраическая кратность каждого корня совпадает с его геометрической кратностью.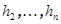 . Матрица линейного преобразования в этом базисе имеет блочный вид
. Матрица линейного преобразования в этом базисе имеет блочный вид  , где
, где  линейное преобразование W, матрица которого в базисе
линейное преобразование W, матрица которого в базисе 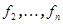 , в котором матрица линейного преобразования имеет верхний треугольный вид. Пусть T – матрица перехода к этому базису. Тогда
, в котором матрица линейного преобразования имеет верхний треугольный вид. Пусть T – матрица перехода к этому базису. Тогда  - верхняя треугольная матрица. Матрица перехода от базиса
- верхняя треугольная матрица. Матрица перехода от базиса  к базису
к базису 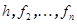 равна
равна 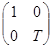 , и, значит, матрица
, и, значит, матрица  , то есть является верхней треугольной.
, то есть является верхней треугольной.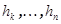 , где k равно либо 2, либо 3. Матрица линейного преобразования в этом базисе имеет блочный вид
, где k равно либо 2, либо 3. Матрица линейного преобразования в этом базисе имеет блочный вид 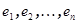 - базис V, в котором матрица линейного преобразования
- базис V, в котором матрица линейного преобразования 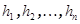 . Матрица перехода T от базиса
. Матрица перехода T от базиса 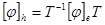 . Поскольку произведение верхних треугольных матриц является верхней треугольной матрицей, то матрица
. Поскольку произведение верхних треугольных матриц является верхней треугольной матрицей, то матрица  - верхняя треугольная. Положим
- верхняя треугольная. Положим 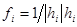 , где i= 1,…, n. Базис
, где i= 1,…, n. Базис 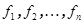 - ортонормированный и матрица линейного преобразования в этом базисе – верхняя треугольная, тем самым теорема доказана.
- ортонормированный и матрица линейного преобразования в этом базисе – верхняя треугольная, тем самым теорема доказана.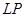 множество всех линейных преобразований пространства V, а через B множество билинейных функций, заданных на V. Если
множество всех линейных преобразований пространства V, а через B множество билинейных функций, заданных на V. Если  , то функция
, то функция 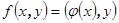 является билинейной. Таким образом, определено однозначное отображение множества линейных преобразований LP в множество билинейных функций B. Исследуем свойства этого отображения.
является билинейной. Таким образом, определено однозначное отображение множества линейных преобразований LP в множество билинейных функций B. Исследуем свойства этого отображения.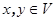 справедливо равенство
справедливо равенство 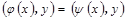 или
или  . Положим
. Положим 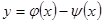 , тогда
, тогда  и
и 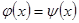 для любого вектора
для любого вектора 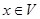 . Это означат, что линейные преобразования равны, что противоречит допущению.
. Это означат, что линейные преобразования равны, что противоречит допущению.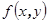 существует линейное преобразование
существует линейное преобразование 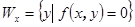 . Ортогональное дополнение к этому подпространству имеет размерность не выше 1. Действительно, если
. Ортогональное дополнение к этому подпространству имеет размерность не выше 1. Действительно, если 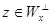 и
и  , то
, то 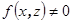 и для вектора
и для вектора  справедливо включение
справедливо включение 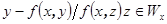 , и, значит
, и, значит  . Определим функцию
. Определим функцию 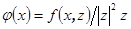 , где z – базис
, где z – базис 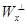 . Если
. Если 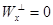 , то положим
, то положим 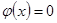 . Легко убедиться, что
. Легко убедиться, что  , и, значит функция
, и, значит функция  - линейное преобразование.
- линейное преобразование. . Это отображение взаимно однозначно.
. Это отображение взаимно однозначно.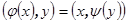 . Сопряженное преобразование к
. Сопряженное преобразование к 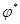 .
. - матрица линейного преобразования
- матрица линейного преобразования 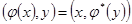 к равенству координат
к равенству координат 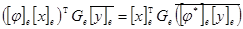 . Из этого равенства выводим
. Из этого равенства выводим  . В случае ортонормированного базиса формула принимает более простой вид
. В случае ортонормированного базиса формула принимает более простой вид 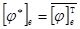 . Для евклидова пространства, знак комплексного сопряжения можно опустить.
. Для евклидова пространства, знак комплексного сопряжения можно опустить.
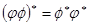
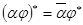

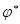 .
. выводим первое свойство. Второе свойство получается из равенств
выводим первое свойство. Второе свойство получается из равенств  . Для доказательства третьего свойства достаточно рассмотреть равенства
. Для доказательства третьего свойства достаточно рассмотреть равенства 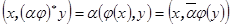 . Четвертое свойство доказывается равенствами
. Четвертое свойство доказывается равенствами  . Докажем пятое свойство. Для произвольного вектора x из W и произвольного вектора
. Докажем пятое свойство. Для произвольного вектора x из W и произвольного вектора 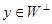 скалярное произведение
скалярное произведение  . По определению сопряженного преобразования
. По определению сопряженного преобразования 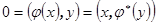 , и, значит
, и, значит  , что и требовалось доказать.
, что и требовалось доказать.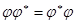 .
. .
. . Поскольку
. Поскольку 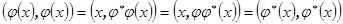 и
и 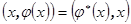 , то
, то 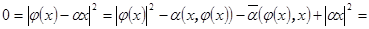
 .
. (
(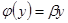 ). Из равенств
). Из равенств 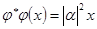 и
и 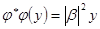 (Свойство 8.22) выводим
(Свойство 8.22) выводим  ,
, 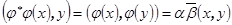 ,
, 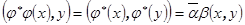 ,
,  . Далее,
. Далее,  , откуда
, откуда 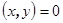 .
. , тогда
, тогда 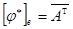 . Из равенства
. Из равенства  вытекает, что матрица A – диагональная, и, значит, базис
вытекает, что матрица A – диагональная, и, значит, базис  . Из равенства
. Из равенства 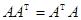 вытекает, что матрица A – блочно диагональная, что и требовалось доказать.
вытекает, что матрица A – блочно диагональная, что и требовалось доказать. является линейным пространством над полем комплексных чисел C. В этом линейном пространстве введем скалярное произведение
является линейным пространством над полем комплексных чисел C. В этом линейном пространстве введем скалярное произведение  . Определим линейное преобразование пространства
. Определим линейное преобразование пространства  как
как  . Пусть
. Пусть  , тогда
, тогда 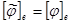 - матрица с вещественными элементами. Далее,
- матрица с вещественными элементами. Далее,  ,
,  и из равенства матриц
и из равенства матриц 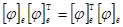 выводим равенство
выводим равенство  , то есть преобразование
, то есть преобразование 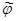 - нормальное. Следовательно, существует ортонормированный базис
- нормальное. Следовательно, существует ортонормированный базис 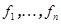 унитарного пространства
унитарного пространства  - собственные числа этих векторов. Заметим, что ортонормированный базис
- собственные числа этих векторов. Заметим, что ортонормированный базис  . Если собственное число
. Если собственное число  является также ортонормированным базисом подпространства
является также ортонормированным базисом подпространства  . Поэтому, не нарушая общности можно считать, что вещественным собственным числам в базисе
. Поэтому, не нарушая общности можно считать, что вещественным собственным числам в базисе 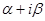 , тогда из равенств
, тогда из равенств  выводим
выводим  ,
,  , то есть линейное подпространство, натянутое на векторы x, y – инвариантно. Из полученных равенств вытекает
, то есть линейное подпространство, натянутое на векторы x, y – инвариантно. Из полученных равенств вытекает  , то есть вектор x - iy – собственный с собственным числом
, то есть вектор x - iy – собственный с собственным числом  . Если
. Если  ортонормированный базис
ортонормированный базис  , то
, то 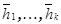 - ортонормированный базис
- ортонормированный базис  , поэтому, можно считать, что в базисе
, поэтому, можно считать, что в базисе  ,
,  собственных векторов с собственными числами
собственных векторов с собственными числами  ортогональны всем остальным векторам. Далее,
ортогональны всем остальным векторам. Далее, 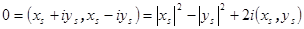 , откуда выводим
, откуда выводим  и
и  . Заменим векторы
. Заменим векторы  и
и  на
на 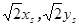 получим ортонормированный базис пространства V, в котором матрица линейного преобразования имеет блочно диагональный вид. По главной диагонали расположены блоки первого порядка, отвечающие вещественным собственным значениям, и блоки второго порядка
получим ортонормированный базис пространства V, в котором матрица линейного преобразования имеет блочно диагональный вид. По главной диагонали расположены блоки первого порядка, отвечающие вещественным собственным значениям, и блоки второго порядка  , отвечающие
, отвечающие  . Из определения выводим
. Из определения выводим  или
или  . Таким образом ортогональное преобразование является нормальным.
. Таким образом ортогональное преобразование является нормальным. , и, значит,
, и, значит,  .
. . Для доказательства осталось заметить, что геометрический смысл указанных преобразований как раз и есть тождественные преобразования, симметрии и повороты в координатных плоскостях.
. Для доказательства осталось заметить, что геометрический смысл указанных преобразований как раз и есть тождественные преобразования, симметрии и повороты в координатных плоскостях. .
. выводим
выводим 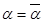 , то есть
, то есть  .
. .
. , и, значит,
, и, значит,  .
. .
. - ортонормированный базис линейного пространства, в котором матрица
- ортонормированный базис линейного пространства, в котором матрица 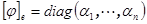 . Все числа стоящие на главной диагонали неотрицательны. Положим
. Все числа стоящие на главной диагонали неотрицательны. Положим  . Легко убедиться, что линейное преобразование
. Легко убедиться, что линейное преобразование  . Если
. Если  называется правым, а разложение
называется правым, а разложение  - левым.
- левым. является самосопряженным и положительно определенным. Построим ортонормированный базис
является самосопряженным и положительно определенным. Построим ортонормированный базис  - собственные векторы с не нулевыми собственными значениями, а
- собственные векторы с не нулевыми собственными значениями, а  - собственные векторы с нулевым собственным значением. Матрица
- собственные векторы с нулевым собственным значением. Матрица  - диагональная, поэтому первые k строк матрицы
- диагональная, поэтому первые k строк матрицы 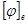 образуют ортогональную систему, а остальные равны 0. Длина j строки равна
образуют ортогональную систему, а остальные равны 0. Длина j строки равна  . Обозначим через
. Обозначим через  первые k строк матрицы
первые k строк матрицы  векторами
векторами  до ортонормированного базиса всего пространства. Обозначим через
до ортонормированного базиса всего пространства. Обозначим через  , а через
, а через  . Легко убедиться, что
. Легко убедиться, что  , то преобразование
, то преобразование  определяется единственным образом.
определяется единственным образом.


