
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Псевдорешения. Метод наименьших квадратов.
Рассмотрим несовместную систему линейных уравнений Ax = b. Псевдорешением системы линейных уравнений называется вектор x, на котором достигается минимум нормы невязки | Ax-b |. Задача построения псевдорешения возникает при подборе параметров физических процессов. Левая часть системы уравнений определяется конкретным видом зависимости от параметров, а правая – конкретными измерениями. Поскольку каждое измерение производится с некоторой точностью, то обычно их проводят с избытком. В результате получается несовместная система линейных уравнений, а задача подбора параметров сводится к построению псевдорешения. Сам способ перехода от задачи решения системы линейных уравнений к нахождению минимума длины невязки называется метод наименьших квадратов. Такое название связано с тем, что Обозначим через W линейную оболочку столбцов матрицы A. Задача построения псевдорешения эквивалентна задаче определения расстояния от b до W,а точнее к определению проекции b на W. Коэффициенты разложения проекции по столбцам матрицы A являются решениями системы уравнений Если исходная система имела решение, то оно является также псевдорешением. Необходимым и достаточным условием единственности псевдорешения является условие линейной независимости столбцов матрицы A. Нормальное решение В ряде случаев, из множества решений, следует выбрать какое то одно. Нормальным решением системы линейных уравнений Ax = b называется решение наименьшей длины. Задача отыскания нормального решения сводится к задаче определения расстояния от начала координат до линейного многообразия, заданного системой линейных уравнений Ax = b. Перпендикуляр, опущенный из начала координат на это линейное многообразие, представляется в виде Нормальное решение всегда единственно, чего нельзя сказать о решении системы
Нормальное псевдорешение. Задача построения нормального псевдорешения сводится к решению системы Унитарное пространство. Пусть V линейное пространство над полем комплексных чисел. Можно ли обобщить понятие скалярного произведения на такое пространство. Оказывается, да! Для этого достаточно незначительно изменить аксиомы скалярного произведения. 1. 2. 3. Черта в свойстве 2 обозначает знак комплексного сопряжения. Пространство над полем комплексных чисел, в котором введено скалярное произведение называется унитарным. Обозначим через G матрицу Грама базисных векторов, то есть матрицу на пересечении строки i столбца j стоит скалярное произведение i-го и j-го вектора
|
|||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 217; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.190.167 (0.005 с.) |
 .
. . Тем самым, задача построения псевдорешения свелась к решению системы линейных уравнений.
. Тем самым, задача построения псевдорешения свелась к решению системы линейных уравнений.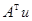 линейной комбинации строк матрицы A. Следовательно, задача построения нормального решения сводится к решению системы линейных уравнений
линейной комбинации строк матрицы A. Следовательно, задача построения нормального решения сводится к решению системы линейных уравнений 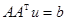 и вычислению ответа
и вычислению ответа 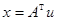 .
.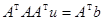 и вычисления нормального псевдорешения по формуле
и вычисления нормального псевдорешения по формуле 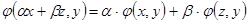 .
.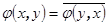
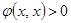 при
при 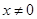 .
.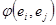 . Используя матричные операции умножения, получаем
. Используя матричные операции умножения, получаем 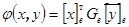 . Матрицы Грама в разных базисах связаны формулой
. Матрицы Грама в разных базисах связаны формулой 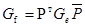 , где P матрица перехода. Все остальные свойства скалярного произведения полностью сохраняются.
, где P матрица перехода. Все остальные свойства скалярного произведения полностью сохраняются.


