
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приведение квадратичных форм (симметричных билинейных форм, эрмитовых форм) к простейшему виду.
4.4.1 Метод выделения квадратов (Лагранжа). Базис Теорема 4.8 Лагранжа. Для любой эрмитовой функции существует канонический базис. Доказательство проведём индукцией по рангу r матрицы эрмитовой формы F. Если r =0, то матрица нулевая, утверждение очевидно. Допустим, что теорема верна для r -1. Докажем ее истинность для r. Рассмотрим три случая а) б) в) 1. 2. Базис эрмитовой билинейной функции f (x,y) называется нормальным, если матрица билинейной функции в этом базисе имеет диагональный вид, и ее главная диагональ равна (1,..,1,-1,..,-1,0..,0). Для отыскания матрицы перехода можно поступать следующим образом. Припишем к матрице F единичную матрицу справа. Затем будем производить элементарные преобразования со строками расширенной матрицы и столбцами матрицы F. Причем, если к строке k прибавим строку j, умноженную на число Следствие 4.11 Для эрмитовой формы существует нормальный базис если поле R или C. Доказательство. Построим канонический базис. Далее, если
Следствие 4.12 Если все угловые миноры матрицы F отличны от нуля, то существует верхняя треугольная матрица Q, которая приводит F к диагональному виду. Доказательство проведем индукцией по рангу F. По теореме Лагранжа существует матрица Q, приводящая F к диагональному виду. Докажем, что она верхняя треугольная матрица. Обозначим через верхняя треугольная матрица Q’, приводящая матрицу 4.4.2 Приведение квадратичных форм к нормальному виду элементарными преобразованиями Симметричные матрицы A и F назовем конгруэнтными, если найдется невырожденная матрица P, что 1. Положим r =1. 2. Если 3. Положим 4. Если найдется i, что 5. Если для всех i,j > r справедливо неравенство Легко проверить, что предложенный алгоритм построит диагональную матрицу конгруэнтную исходной матрице. Преобразованиями вида
Если приписать справа единичную матрицу, то элементарные преобразования можно запомнить в ней.
|
||||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 135; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.113.30 (0.005 с.) |
 называется каноническим для симметричной (эрмитовой) билинейной функции, если ее матрица в этом базисе диагональная.
называется каноническим для симметричной (эрмитовой) билинейной функции, если ее матрица в этом базисе диагональная. , тогда положим
, тогда положим  и
и  , где k >1. В данном случае матрица перехода S будет отличаться от единичной матрицы только первой строкой, равной
, где k >1. В данном случае матрица перехода S будет отличаться от единичной матрицы только первой строкой, равной  и S [ x ]=[ x ’], Q [ x ’]=[ x ], где
и S [ x ]=[ x ’], Q [ x ’]=[ x ], где  . Матрица Q отличается от единичной матрицы только первой строкой, равной (1,
. Матрица Q отличается от единичной матрицы только первой строкой, равной (1,  ,…,
,…,  ). После замены координат, получим матрицу билинейной формы
). После замены координат, получим матрицу билинейной формы  , которая имеет следующий блочный вид
, которая имеет следующий блочный вид  . Поскольку ранг
. Поскольку ранг  равен r -1, то по предположению индукции эрмитову матрицу
равен r -1, то по предположению индукции эрмитову матрицу  . Тогда
. Тогда  и теорема в этом случае доказана.
и теорема в этом случае доказана. и существует k, что
и существует k, что  переставим первый и k базисные вектора, и далее перейдем к пункту а).
переставим первый и k базисные вектора, и далее перейдем к пункту а). для всех k и найдётся не нулевой элемент
для всех k и найдётся не нулевой элемент  , где
, где  . Возможны два случая:
. Возможны два случая: тогда прибавим к k базисному вектору l базисный вектор и получим случай б)
тогда прибавим к k базисному вектору l базисный вектор и получим случай б) тогда прибавим к k базисному вектору l базисный вектор, умноженный на i, и получим случай б). Теорема доказана.
тогда прибавим к k базисному вектору l базисный вектор, умноженный на i, и получим случай б). Теорема доказана. , то затем к столбцу k прибавим столбец j, умноженный на число
, то затем к столбцу k прибавим столбец j, умноженный на число  . После приведения матрицы F к диагональному виду справа будет расположена матрица, все элементы которой комплексно сопряжены к матрице перехода.
. После приведения матрицы F к диагональному виду справа будет расположена матрица, все элементы которой комплексно сопряжены к матрице перехода. , то умножим j базисный вектор на число
, то умножим j базисный вектор на число  . Затем перестановкой базисных векторов приведем матрицу к нормальному виду.
. Затем перестановкой базисных векторов приведем матрицу к нормальному виду.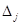 угловой минор j -го порядка матрицы F. Так как
угловой минор j -го порядка матрицы F. Так как  , то выполняется пункт а) теоремы Лагранжа. Матрица перехода Q верхняя треугольная. Угловой минор матрицы
, то выполняется пункт а) теоремы Лагранжа. Матрица перехода Q верхняя треугольная. Угловой минор матрицы  , равен
, равен  (угловому минору порядка k матрицы F). По предположению индукции, найдется
(угловому минору порядка k матрицы F). По предположению индукции, найдется - верхняя треугольная матрица, а
- верхняя треугольная матрица, а  - диагональная матрица.
- диагональная матрица. . Матрицы билинейной формы в различных базисах конгруэнтны. Из теоремы Лагранжа вытекает, что симметричная квадратная матрица конгруэнтна диагональной матрице diag (1,…,1.-1,…,-1,0,…,0). Опишем алгоритм приведения симметричной квадратной матрицы F к диагональному виду элементарными преобразованиями. Отметим, если мы совершаем какие то действия со строками матрицы F, то те же самые действия надо совершить и со столбцами матрицы. Номера столбцов будут указываться в квадратных скобках, а номера строк – в круглых скобках.
. Матрицы билинейной формы в различных базисах конгруэнтны. Из теоремы Лагранжа вытекает, что симметричная квадратная матрица конгруэнтна диагональной матрице diag (1,…,1.-1,…,-1,0,…,0). Опишем алгоритм приведения симметричной квадратной матрицы F к диагональному виду элементарными преобразованиями. Отметим, если мы совершаем какие то действия со строками матрицы F, то те же самые действия надо совершить и со столбцами матрицы. Номера столбцов будут указываться в квадратных скобках, а номера строк – в круглых скобках. , то перейдем на шаг 4, иначе шаг 3.
, то перейдем на шаг 4, иначе шаг 3. ,
,  , где
, где  . Затем увеличим r на 1 и вернемся на шаг 2.
. Затем увеличим r на 1 и вернемся на шаг 2. , то положим
, то положим  ,
,  и вернемся на шаг 2. В противном случае перейдем на шаг 5.
и вернемся на шаг 2. В противном случае перейдем на шаг 5. , то алгоритм работу закончил. В противном случае найдутся номера i,j, для которых
, то алгоритм работу закончил. В противном случае найдутся номера i,j, для которых  . Тогда переставим строки
. Тогда переставим строки 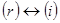 и столбцы
и столбцы  и вернемся на шаг 2.
и вернемся на шаг 2. ,
,  можно добиться, чтобы на главной диагонали стояли только 0,1,-1. Перестановками строк и столбцов элементы матрицы, стоящие по главной диагонали, можно расположить в порядке не возрастания.
можно добиться, чтобы на главной диагонали стояли только 0,1,-1. Перестановками строк и столбцов элементы матрицы, стоящие по главной диагонали, можно расположить в порядке не возрастания.


