
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Закон инерции квадратичных форм.
Теорема 4.9 Закон инерции. Для любой эрмитовой билинейной функции нормальный вид определяется единственным образом. Доказательство проведем методом от противного. Пусть найдется два базиса Число положительных слагаемых в нормальном виде эрмитовой формы называется положительным индексом инерции, а число слагаемых с отрицательными коэффициентами – отрицательный индекс инерции. Индексы инерции эрмитовых форм не зависят от выбора базиса. Теорема Якоби Обозначим через Теорема 4.10 Якоби. Пусть Доказательство очевидным образом повторяет Следствие 4.12. Критерий Сильвестра. Эрмитовая форма Теорема 4.11 Критерий Сильвестра положительной определенности. Эрмитова форма положительна определена тогда и только тогда, когда все ее главные миноры (расположенные по главной диагонали) строго больше нуля. Доказательство. Если все главные миноры F строго больше нуля, то и все угловые миноры матрицы F строго больше нуля. По теореме Якоби найдется базис, в котором эрмитова форма имеет вид Покажем обратное. Допустим, найдется главный минор матрицы F, не больше нуля. Не нарушая общности можно считать, что это угловой минор порядка k, так как в противном случае перенумеруем переменные соответствующим образом. Далее, можно считать, что все угловые миноры до (k -1)-го порядка больше нуля. Действительно, иначе можно положить k равным меньшему значению. Положим все переменные с номером больше k равными нулю. В результате получим эрмитову форму от k переменных с матрицей
Квадрики. Алгебраическая поверхность Пусть Под аффинной заменой координат будем понимать замену вида Теорема 5.12При аффиной заменой координат порядок поверхности не меняется. Доказательство. Непосредственной подстановкой легко проверить, что при аффинной замене координат порядок поверхности не возрастает. Возврат к исходной системе координат является аффинным преобразованием. Значит, порядок поверхности не может и убывать. Уравнение квадрики. Алгебраическая поверхность второго порядка называется квадрикой. Общее уравнение квадрики можно записать в следующем виде 5.3 Изменение квадрики при аффинном преобразовании Ответим на вопрос об изменении уравнения квадрики при аффинной замене координат x = h + Ty. Положим Теорема 5.13. Пусть из квадрики Обозначим через s (A) положительный индекс инерции, а через t (A) – отрицательный индекс инерции квадратичной формы. Из приведенных формул вытекает полезное следствие. Следствие 5.13. Пусть из квадрики
Доказательство вытекает из закона инерции квадратичных форм и формул изменения квадрики при аффинной замене системы координат. Следствие 5.14. Величины
|
||||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 152; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.119.251 (0.005 с.) |
 и
и  , в которых нормальный вид различный. Пусть
, в которых нормальный вид различный. Пусть  и
и  и
и  . Поскольку
. Поскольку  , то нормальный вид различен только если
, то нормальный вид различен только если  . Для определенности положим
. Для определенности положим  . Обозначим через W линейную оболочку векторов
. Обозначим через W линейную оболочку векторов  , а через U – линейную оболочку векторов
, а через U – линейную оболочку векторов 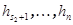 . Для не нулевого вектора
. Для не нулевого вектора  имеем
имеем  и
и  , а для вектора
, а для вектора  выполняются равенства
выполняются равенства  и
и  . Пересечение подпространств
. Пересечение подпространств  не может содержать векторов отличных от нуля, но
не может содержать векторов отличных от нуля, но  . К полученному противоречию привело допущение
. К полученному противоречию привело допущение 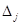 угловой минор j -го порядка матрицы F (и положим
угловой минор j -го порядка матрицы F (и положим 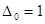 ).
).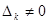 (k =1,2,.., r). Существует канонический базис
(k =1,2,.., r). Существует канонический базис  , для которого
, для которого 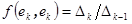 , при k =1,2,.., r, и
, при k =1,2,.., r, и 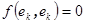 при k > r.
при k > r.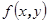 называется положительно определенной, если для любого
называется положительно определенной, если для любого 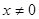 справедливо неравенство
справедливо неравенство 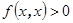 .
.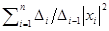 . Поскольку все коэффициенты строго больше нуля, то эрмитова форма положительно определена.
. Поскольку все коэффициенты строго больше нуля, то эрмитова форма положительно определена. . Угловые миноры этой матрицы до (k -1)-го порядка больше нуля, и, значит можно воспользоваться теоремой Якоби. В некотором базисе эта форма имеет вид
. Угловые миноры этой матрицы до (k -1)-го порядка больше нуля, и, значит можно воспользоваться теоремой Якоби. В некотором базисе эта форма имеет вид  . По построению
. По построению  , и, значит, найдется не нулевой вектор, значение эрмитовой формы
, и, значит, найдется не нулевой вектор, значение эрмитовой формы 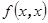 на котором не больше нуля, что противоречит ее положительной определенности. К полученному противоречию привело допущение о существовании не положительных главных миноров матрицы F. Следовательно, все главные миноры больше нуля.
на котором не больше нуля, что противоречит ее положительной определенности. К полученному противоречию привело допущение о существовании не положительных главных миноров матрицы F. Следовательно, все главные миноры больше нуля.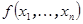 некоторый полином от n переменных. Алгебраической поверхностью называется множество решений уравнения
некоторый полином от n переменных. Алгебраической поверхностью называется множество решений уравнения  , порядком алгебраической поверхности называется максимальная степень полинома. Если n =2, то алгебраическая поверхность называется алгебраической кривой.
, порядком алгебраической поверхности называется максимальная степень полинома. Если n =2, то алгебраическая поверхность называется алгебраической кривой.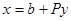 , где P – невырожденная матрица.
, где P – невырожденная матрица.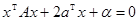 . Положим
. Положим 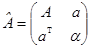 и
и  . Уравнение квадрики в новых обозначениях принимает вид
. Уравнение квадрики в новых обозначениях принимает вид 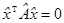 . Матрица
. Матрица 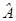 называется расширенной матрицей квадрики.
называется расширенной матрицей квадрики.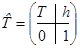 , тогда равенство x = h + Ty эквивалентно равенству
, тогда равенство x = h + Ty эквивалентно равенству  , и, значит,
, и, значит, 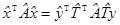 . Тем самым установлена теорема.
. Тем самым установлена теорема.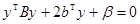 , тогда
, тогда 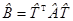 ,
, 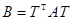 ,
,  ,
, 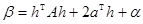 .
.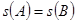 ,
, 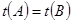 ,
, 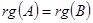 и
и 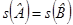 ,
, 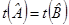 ,
, 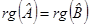 .
.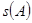 ,
, 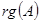 ,
, 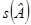 ,
, 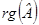 являются аффинными инвариантами квадрики.
являются аффинными инвариантами квадрики.


