
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Самочинне (спонтанне) і вимушене випромінюванняСодержание книги
Поиск на нашем сайте
Процеси випромінювання і поглинання фотонів можна вивчати менш детально, спираючись на теорію випромінювання, яка була розвинена Ейнштейном у 1917 р. і на теорію квантових переходів. Таке уявлення засноване на законах збереження енергії (1) і імпульсу (2) при взаємодії квантових систем з електромагнітним випромінюванням: ħω + Е = ћω' + Е' (1) ħ'к + р = ћк' + р', (2) де Е і р – енергія і імпульс системи до взаємодії з квантом світла, Е', р' – після взаємодії, аналогічно ħω, ħ'к – енергія і імпульс фотона до взаємодії… ћω', ћк' – після…
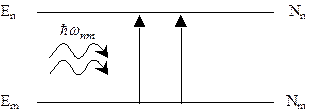
Безпосередній квантовий перехід (дозволений першому наближенні теорії збурень) з одного квантового стану в інший, можливий, якщо в електромагнітному випромінюванні присутні ЕМХ з частотами, які задовольняють правилам частот Бора. Нехай маємо 2 енергетичних рівні з енергіями Еm>Еn, в яких може знаходитись квантова система, тоді на основі закону збереження енергії можливі 3 ситуації: 1) Е = Еm; Е' = Еm > Еn; ћω' = ħωmn = Еm - Еn; Тоді фотони з енергією ħω ≠ Еm - Еn у взаємодії не приймають участь. Тому можна записати ħω = 0. Це означає, що система в результаті взаємодії перейшла у більш низький енергетичний стан. Такий процес називається спонтанним випусканням (випромінюванням) (испусканием) фотона. 2) Е = Еn; Е' = Еm > Еn; ћω = ħωmn = Еm - Еn; ћω' = 0; В цьому випадку фотон з енергією ћω збуджує систему і переводить її з більш низького у більш високий енергетичний стан з поглинанням кванта світла. Такий процес називається резонансним поглинанням світла. 3) Е = Еm; Е' = Еn< Еm; ћω = ћω' = ħωmn = Еm - Еn. В цьому випадку фотон з енергією ħω = Еm-Еn не зникає, а в результаті взаємодії виникає додатковий фотон з енергією ћω' = ħω = Еm-Еn, тоді в правій частині рівняння (.1) додатково буде 2ħωmn. Система в результаті взаємодії перейшла з більш високого в більш низький рівень з випромінюванням кванта світла з частотою, яка дорівнює частоті переходу. В якості змушуючого фактора, який визначає подібний перехід, виступає фотон, з тією ж частотою, що й випромінений. Тому такий перехід називається вимушеним випромінюванням фотону. На перелічених 3 елементарних процесах взаємодії електромагнітного випромінювання з квантовими системами (схематично зображених на рис.) заснована робота більшості приладів квантової і оптичної електроніки.
Примусовим фактором, який призводить до спонтанного випромінювання, є зовнішнє випромінювання, причому фотон з частотою ωmn=(Еm - En)/ħ, тому обидва ці квантові переходи називаються вимушеними. Примусовим фактором, який призводить до спонтанного (самочинного) випромінювання фотона, в явному виді не присутній, і такий квантовий перехід називається спонтанним (самочинним). Спонтанне випромінювання виникає внаслідок самочинного квантового переходу атома (або іншої квантової системи) із збудженого стану в основний, або інший збуджений стан з меншою енергією. Спонтанний перехід – це мимовільний перехід частки з більше високого Е n на більше низький рівень Е m (мал. 1).
Перехід супроводжується випущенням кванта енергії із частотою wnm. Для протікання цього процесу наявність зовнішнього поля не потрібно. Ймовірність спонтанного переходу не залежить від зовнішнього поля, і визначається властивостями атома або молекули. Імовірність спонтанного переходу в одиницю часу зі стану Е n у стан Е m називається коефіцієнтом Ейнштейна для спонтанного випромінювання Аnm, тобто d Аmn – коефіцієнт Ейнштейна для самочинних переходів. Його значення не залежить від зовнішніх взаємодій і визначається тільки властивостями даної квантової системи. Спонтанний час життя (середній час життя) атома іона або молекули в збудженому стані назад пропорційно ймовірності спонтанного переходу t =1/Anm. Величину t ще називають спонтанним часом життя для переходів Слід зазначити (!), що спонтанне випромінювання неспрямоване, некогерентне і немонохроматичне. Воно служить джерелом шумів, нестабільності коливань, але разом з тим, що дуже важливо, спонтанні переходи сприяють початку процесу посилення й порушення коливань у мазерах і лазерах, і відіграють важливу роль при одержанні нерівновагих станів у квантовій системі. Спонтанне випромінювання описує процес мимовільного переходу частки з верхнього стану в нижній. Мимовільних переходів знизу вгору не буває. Заселення верхнього рівня відбувається в розглянутій ситуації шляхом індукованих переходів при поглинанні квантів енергії. Спонтанне випромінювання в оптичному діапазоні випромінюють усі класичні джерела світла (лампи накалювання, газорозрядні лампи, люмінесцентні лампи). Вимушені (індуційні) переходи відбуваються під впливом зовнішнього поля випромінювання резонансної частоти й залежать від спектральної щільності енергії зовнішнього поля r (w) [Дж/(див3×Гц)]. При вимушеному переході з нижнього рівня на верхній (малюнок 3) квант енергії поглинається із частотою
В результаті вимушеного випромінювання атом віддає енергію електромагнітних хвиль, амплітуда якої збільшується. Ймовірність таких переходів в одиницю часу дорівнює dWnm погл = Bnm ρ(ω)dt, де Bnm – коефіцієнт Ейнштейна для вимушених переходів з поглинанням; ρ(ω) – спектральна щільність випромінювання з частотою
Рис. 3 Середній час життя атома щодо індукованого переходу n(m назад пропорційно величині Таким чином, при вимушених переходах квантова система може переводитися з одного енергетичного стану в інший як з поглинанням енергії електромагнітного поля, так і з випромінюванням електромагнітної енергії. Імовірність спонтанного переходу в одиницю часу пов'язана з імовірністю вимушеного переходу між станами співвідношенням
де dnm – мат. Електронний дипольний момент. А ймовірності індукованих переходів з випромінюванням (n®m) і поглинанням (m®n) енергії рівні між собою, тобто Bnm = Bmn. Коефіцієнт Безвипромінювальні переходи
Крім випромінювальних переходів, пов'язаних з поглинанням і випромінюванням кванта енергії, у системі квантових часток можливі безвипромінювальні переходи, при яких енергія атома передається іншим атомам або навколишньому середовищу (виникають при зіткненні атомів і молекул у газі, як один з одним, так і з електронами або стінками посудини, переходи в твердому тілі при взаємодії з коливаннями кристалічної решітки й т.д.). У результаті такої взаємодії атом, іон або молекула переходить зі стану n у стан m або навпаки без випромінювання кванта й без його участі (малюнок 5а,б).
а) б) Рис. 5 Ймовірність безвипромінювального переходу з верхнього рівня на нижній прийнято позначати wnm, з нижнього на верхній wmn. Ймовірності безвипромінювальних переходів між рівнями n
Середній час життя атома Якщо квантова частинка робить перехід зі збудженого стану n, у результаті різних процесів (спонтанних, індукованих, безвипромінювального переходів), що характеризується часом життя t 1=1/ Аmn, t 2 =1/ Bmnr (w), t 3=1/wmn і ці процеси статистично незалежні, то середній час життя частки в стані n пов'язане із часами життя для інших процесів співвідношенням
ЗВ'ЯЗОК МІЖ КОЕФІЦІЄНТАМИ ЕЙНШТЕЙНА
Розглянемо сукупність атомів (молекул), які знаходяться в термодинамічній рівновазі зі стінками оточуючого об’єму при температурі Т. Нехай на рівні Еm знаходиться Nm частинок, а на рівні Еn - Nn частинок. Тоді число поглинутих квантів за інтервалом dt буде
Число квантів світла, які будуть випромінені в результаті спонтанних переходів:
а кількість квантів світла, які випущені в результаті вимушеного випромінювання
При термодинамічній рівновазі ансамбль квантових часток не втрачає і не здобуває енергію. Отже, умова термодинамічної рівноваги означає, що загальна кількість квантів світла, які випромінені системою, дорівнює числу поглинутих квантів світла:
Загальне число переходів визначається числом часток на рівнях енергії. При тепловій рівновазі розподіл часток по рівнях підкоряється формулі Больцмана
де g1 і g2 – статистична вага рівнів 1 і 2 (для невироджених рівнів gn = gm = 1); k - постійна Больцмана 1,38*10-23 Дж/K. Частки розглянутого ансамблю перебувають у поле їхнього власного випромінювання, щільність енергії якого в одиничному спектральному інтервалі становить r (w). Це поле индуцирует переходи з верхнього стану в нижнє й назад. Імовірності цих переходів пропорційні r (w)
Комбінуючи (2) і (3) з умови термодинамічної рівноваги (сумарне число квантів, що випускаються системою дорівнює числу квантів світла, що поглинаються,)
Можна знайти співвідношення між коефіцієнтами Anm, Bnm, Bmn. У рівнянні (4) прирівняний друг до друга повні числа переходів знизу нагору (ліворуч) і зверху вниз (праворуч). Це рівняння дозволяє чітко знайти щільність енергії поля випромінювання розглянутої рівноважної квантової системи:
Звідси випливають важливі наслідки! Ейнштейн постулировал, що випромінювання, що випускається й поглинає при рівноважних переходах між енергетичними станами розглянутої рівноважної квантової системами, описується формулою Планка для рівноважного випромінювання абсолютно чорного тіла
Іноді формулу Планка записують не для (((), а для (((), при цьому ((()=((()/2(. Порівнюючи ці дві формули з урахуванням умови Бору (Е2-І1 = g 1 B 12= g 2 B 21. (7) Це співвідношення говорить про равновероятности індуковані випромінювання й поглинання (у перерахуванні на одне невырожденное стан). А ймовірність спонтанного випромінювання пропорційна коефіцієнту Ейнштейна для індукованого випромінювання:
Імовірність спонтанного переходу в одиницю часу пов'язана з імовірністю змушеного переходу між станами співвідношенням
а ймовірності індукованих переходів з випромінюванням (n®m) і поглинанням (m®n) енергії рівні між собою, тобто B nm = B mn. Коефіцієнт Таким чином, установлений зв'язок між коефіцієнтами Ейнштейна, але не саме їхнє значення. Це буде зроблено пізніше. Можна тепер записати, що повна ймовірність переходу вниз для збудженої частки з випущенням квантів випромінювання дорівнює
Істотно, що Рівноважне випромінювання всього ансамблю часток стосовно кожної із часток виступає як зовнішнє електромагнітне поле, що стимулює поглинання або випромінювання часткою енергії залежно від її стану. Тому співвідношення (8-10), отримані при розгляді умов рівноваги, справедливі й для випадку квантової системи, що перебуває в поле зовнішнього випромінювання. Ще одне зауваження. З (9) треба, що ймовірність спонтанних переходів сильно залежить від частоти - як куб частоти. Звідси треба, що в області СВЧ, де працюють парамагнітні мазери, роль спонтанних переходів невелика й, як наслідок, - дуже низький шум таких підсилювачів. В оптичному діапазоні частот роль спонтанних переходів різко зростає, вони є джерелом шумів, причиною дуже малих часів життя збуджених станів, що утрудняє, а іноді й унеможливлює роботу підсилювачів і генераторів. У всякому разі, в оптичному й белее короткохвильових діапазонах довжин хвиль зі спонтанними переходами доводиться вважатися істотно. Отже з ростом частоти ймовірність спонтанного переходу різко зростає.
В загальному випадку, якщо спустошення збудженого стану m проходить за рахунок різних незалежних процесів, які характеризуються сталими часу τ1, τ2,…... τ∞ або ймовірностей середній час життя атома у збудженому стані m:
Ймовірність переходу пов’язана з відповідним матричним елементом і для оптичних переходів цей зв'язок найбільш виразно проявляється при порівнянні класичного і квантового осциляторів. При цьому виконується дипольне наближення.
ДИПОЛЬНЕ ВИПРОМІНЮВАННЯ
З погляду випромінювання і поглинання електромагнітної енергії атом можна розглядати як мультіпольну систему. За визначенням, мультиполь є системою парних, різнойменних зарядів, що володіє певною симетрією. Система двох зарядів - це диполь, чотири - квадруполь, восьми - октуполь і т.д. Кожен мультиполь характеризується своїм моментом, порядок n якого пов'язаний з повним числом зарядів N співвідношенням N = 2n. Довільний розподіл зарядів в загальному випадку можна представити у вигляді ряду, члени якого складають моменти різних порядків. Таке уявлення виявляється зручним для опису випромінюючих властивостей атомів і молекул. У оптичному діапазоні довжина електромагнітної хвилі багато більше розмірів атома і ряд швидко сходитиметься із збільшенням порядку мультиполя. Як показують розрахунки, для видимої області (λ = 0,5∙10-6 м) квадрупольне випромінювання слабше дипольного ~ в 106 разів. З погляду класичних уявлень простим джерелом електромагнітного випромінювання є точковий заряд, рухомий з прискоренням. Енергія Е, випромінювана зарядом е в одиницю часу, пропорційна квадрату прискорення а:
Якщо заряд виконує гармонічні коливання з частотою ω та амплітудою rm т.б. r(t) = rm cos ωt, (2) то з (1) отримуємо миттєву потужність випромінювання: Р= -
Середня по часу за період коливань потужність випромінювання:
Рис.1 Середня потужність випромінювання такого осцилятора виходить з виразу (4):
де Do — амплітуда зміни дипольного моменту.
Багато оптичних властивостей випромінюючих систем можна отримати, моделюючи такі системи сукупністю гармонійних осциляторів, власні частоти яких співпадають з частотами даних переходів.
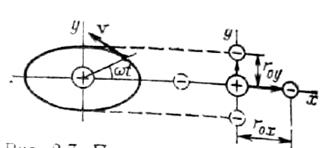
Рис. 2
Як видно з рис. 2, такий рух можна замінити гармонійними коливаннями двох диполів (лінійних осциляторів), власні частоти яких рівні кутовій швидкості обертання електрона по орбіті, а фази здвинуті на кут π/2. Дипольні моменти таких випромінювачів рівні: Dx = - er0x cos ω0 t, Dy = - er0y sin ω0 t. З погляду класичної електродинаміки осцилюючий диполь випромінює енергію безперервно. Амплітуда коливань для класичного осцилятора може приймати будь-які значення. В початковий момент часу t=0 осцилятор володіє запасеною енергією E0, чому відповідає амплітуда коливань r0, причому
З часом такий класичний осцилятор передає енергію полю згідно із законом (3). Цьому відповідає зменшення амплітуди коливань rm. При t > 0 Порівнюючі цей вираз з (5), отримуємо < Р >= - Вводячи позначення
отримуємо рівняння для енергії випромінювача
Звідси
Зміна амплітуди коливань класичного осцилятора в часі:
графік цієї залежності
З (10) знаходимо, що середня за період потужність випромінювання електричного диполя змінюється в часі по експоненціальному закону:
де (13)
Миттєва потужність випромінювання диполя пропорційна r2(t). Очевидно, така система випромінює немонохроматичну хвилю (див. рис. 2). Для визначення спектру випромінювання г(t) слід представити у вигляді інтеграла Фурье, тобто функцію (12), зображену на мал. 2., представити у вигляді суми (інтеграла) гармонійних складових.
де
Залежність (12) можна записати в експоненціальній формі:
І підставивши в цей вираз в (15), отримуємо
Тоді |r (ω) |2 = r* (ω) r (ω) = де ω0 – власна (резонансна) частота осцилятора, ro - початкова амплітуда коливань при t=0.
Залежність
де А - множник нормування, називається кривою Лоренца, А=γ/2π Вона визначає розподіл енергії після частотному спектру. Функція Лоренца представлена на рис. 3.
Величина 2 (ω0- ω0) = Δω0 =γ, називається напівшириною лінії, представляє собою природню ширину спектральної Рис.3 лінії. Так як γ = 1/τ, де τ – час релаксації,то Δω τ ≈ 1. Розглянемо тепер квантовий осцилятор. Його до енергія на відміну від класичного осцилятора може приймати тільки певні дискретні значення. Тут не може бути плавної зміни амплітуди коливань, а присутній стрибкоподібний перехід з одного дозволеного стану в інший. Частота випромінювання квантового осцилятора визначається через енергію переходу: ωmn = (Em-En)/ħ Такому переходу відповідає виникнення осцилюючого електричного моменту атома. Середнє значення електричного дипольного моменту
а його проекції:
r - радіус-вектор, проведений з початку координат, в якому поміщено ядро атома. Під час переходу атома із стану т в стан п розподіл заряду визначається хвильовими функціями обох станів:
Об'ємна щільність заряду при переході з одного квантового стану в інше осцилює з характерною частотою ωmn = (Em-En)/ħ. Такий розподіл заряду можна характеризувати інтегральним дипольним моментом
Для стаціонарного стану дипольний момент постійний в часі. При переході з одного стану в інше виникають осциляції дипольного моменту
Таким чином, квантовий перехід із стану m в стан n можна порівняти з появою осцилюючого диполя з власною частотою коливання ωmn. Амплітуда дипольного моменту
Ця величина кількісно характеризує вірогідність переходу і називається дипольним матричним елементом переходу т→п. Сукупність квантових переходів в квантовій системі характеризується двомірною сукупністю чисел Dmn. Цю сукупність прийнято записувати у вигляді нескінченної матриці
Числа, складові матриці, називаються матричнимі елементами. Потужність випромінюючу при спонтанному переході m→n можна обчислити за допомогою отриманого для класичного осцилятора виразу
якщо замість амплітуди класичного дипольного моменту D0 підставити подвоєний матричний елемент D Вважаючи, що в одиниці об'єму є Nm диполів отримуємо
Величина Nm - населеність верхнього енергетичного рівня. Враховуючи зв'язок між випромінюваною потужністю і вірогідністю спонтанного переходу
Цей вираз відповідає випромінюванню осцилятора з дипольним моментом Dmn = 2ermncosωmnt де
Тоді коефіцієнт Ейнштейна при випромінюванні
Співвідношення (22) і (23) дозволяють розрахувати коефіцієнти Ейнштейна, якщо відомі характеристики (хвильові функції і енергії) станів, між якими відбувається оптичний перехід. Таким чином, коефіцієнти Ейнштейна, вірогідність спонтанних і вимушених переходів визначається через відповідні дипольні матричні елементи, які є недіагональними елементами матриці (21). Деякі з цих матричних елементів можуть дорівнювати нулю. Це означає, що такий перехід не може відбуватися в дипольному наближенні, тому його називають забороненим. Переходи, для яких Dmn ≠ 0 називаються дозволеними. Приналежність переходу до заборонених або дозволених визначається правилами відбору. Для атомних рівнів, що характеризуються квантовими числами n, l і ml, правила відбору для дипольних переходів наступні. 1. Зміна головного квантового числа може бути будь-яким: Δn = 0, 1, 2, …………. 2. Орбітальне квантове число l може змінюватися тільки на ±1: Δ l = ± 1. Це правило по суті відображає закон збереження моменту кількості руху для системи електрон+фотон, оскільки момент кількості руху фотона рівний ħ. 3. Магнітне квантове число ml може змінюватися тільки на 0 або ±1: Δ ml=0; ±1. Аналогічні правила існують і для квантових чисел L (сумарне орбітальне квантове число), S (сумарне спінове число) і J (повний момент системи Перехід буде дозволений, якщо виконуються всі правила відбору. Якщо переходи дозволені в дипольному наближенні, то для них Аmn має порядок величини, 108 с-1. Відповідно час життя системи в такому стані ~ 108 с-1, якщо релаксація із збудженого стану визначається тільки спонтанними випромінювальними переходами, або < 108 с-1, якщо є інші (наприклад, безвипромінюючі) процеси спустошення рівня. Такі рівні з малими часом, життя називаються лабільними. Якщо переходи заборонені в дипольному наближенні, тобто Dmn=0, це не означає, що вони взагалі не можуть відбутися. Окрім електричного дипольного моменту і пов'язаного з ним дипольного випромінювання атому можна приписати електричний квадрупольний (октупольний) або магнітний дипольний (квадрупольний) момент. Матричні елементи і відповідно вірогідності електричного квадрупольного і магнітного дипольного переходів приблизно в 106 разів менше, ніж для електричного дипольного наближення (якщо і ті та інші дозволені, правилами відбору). Вірогідність октупольних переходів, тобто переходів із зміною моменту третього порядку, ще менше. Збуджений енергетичний стан системи, для якого всі переходи в нижчі стани заборонені при електричних дипольних взаємодіях, називається метастабільним рівнем. Час життя атомів в цьому стані близько 10-3 с і більше. Для повного визначення стаціонарного стану електрона в атомі необхідно стільки квантових чисел, скільки має електрон ступенів вільності, т.б. необхідно чотири квантових числа. Для атомів з одним валентним електроном стан електрона однозначно визначає і стан самого атома. У багатоелектроних атомах і іонах стан описується сумарними квантовими числами, які залежать від типу взаємодії між електронами. У таблиці наведені квантові числа електрона й атома, їхнє значення й фізичний зміст.
Такі класичні класифікації атомних рівнів заснована на поданні того, що орбітальні моменти електронів складаються в повний орбітальний момент L атома, а їхні спінові моменти - у повний спин S. Відповідний тип взаємодії при якому дана класифікація виявляється справедливої, називають нормальною або LS -зв'язком. Енергія атома визначається в основному його сумарним орбітальним і спіновим моментами. Енергетичний стан атома із заданими квантовими числами L і S називають спектральним термом. Кожний терм вырожден відповідно різними можливими напрямками векторів L і S у просторі. Кратність виродження дорівнює
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 584; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.198.75 (0.01 с.) |



 = Аmndt,
= Аmndt, 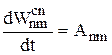
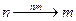 .
.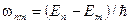 .
.
 .,
.,
 т. б.
т. б.  .
. ,
, 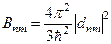 ,
, 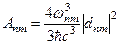 , (11)
, (11)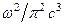 є число типів коливань в одиничному об'ємі й в одиничному інтервалі частот для вільного простору.
є число типів коливань в одиничному об'ємі й в одиничному інтервалі частот для вільного простору.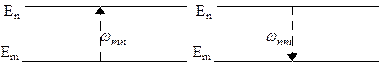
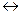 m зв'язані рівністю
m зв'язані рівністю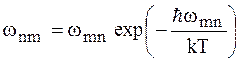 .
.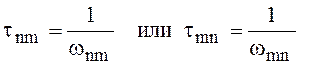 .
.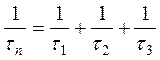 .
. .
.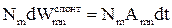 ,
,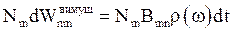 .
. або
або  (1)
(1) , (2)
, (2) . (3)
. (3)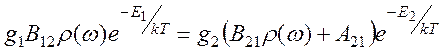 . (4)
. (4)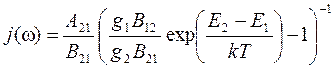 . (5)
. (5) . (6)
. (6)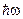 ) Одержуємо:
) Одержуємо: . (8)
. (8) , w=2πν, ν=с/λ с-швидкість світла 3*108 м*с-1 (9)
, w=2πν, ν=с/λ с-швидкість світла 3*108 м*с-1 (9) є число типів коливань в одиничному об'ємі й в одиничному інтервалі частот для вільного простору.
є число типів коливань в одиничному об'ємі й в одиничному інтервалі частот для вільного простору. . (10)
. (10)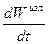 пропорційно В21, і, отже, там, де заборонені індуковані переходи, не може бути й спонтанного випромінювання й навпаки, де немає спонтанного випромінювання, там не може бути індукованого випромінювання.
пропорційно В21, і, отже, там, де заборонені індуковані переходи, не може бути й спонтанного випромінювання й навпаки, де немає спонтанного випромінювання, там не може бути індукованого випромінювання.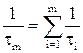
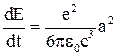 . (1)
. (1)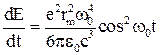 . (3)
. (3)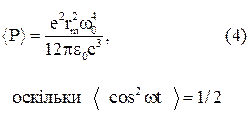
 Ця формула справедлива і для випромінювання, створеного системою з багатьох зарядів. Простою системою є електричний диполь — сукупність двох однакових по величині і протилежних по знаку за рядів, що знаходяться на відстані L один від одного.
Ця формула справедлива і для випромінювання, створеного системою з багатьох зарядів. Простою системою є електричний диполь — сукупність двох однакових по величині і протилежних по знаку за рядів, що знаходяться на відстані L один від одного.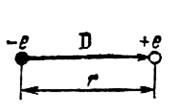 Момент електричного диполя D, або дипольний момент чисельно дорівнює: D=eL і направлений від негативного полюсу до позитивного (рис. 1).
Момент електричного диполя D, або дипольний момент чисельно дорівнює: D=eL і направлений від негативного полюсу до позитивного (рис. 1). Якщо дипольний момент D гармонійно змінюється з частотою ω, то такий диполь називають осцилюючим диполем або осцилятором.
Якщо дипольний момент D гармонійно змінюється з частотою ω, то такий диполь називають осцилюючим диполем або осцилятором.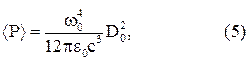
 Розглянемо електрон, рухомий по еліптичній орбіті навколо позитивно зарядженого ядра.
Розглянемо електрон, рухомий по еліптичній орбіті навколо позитивно зарядженого ядра.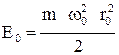 (6)
(6) (7)
(7)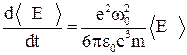 . (8)
. (8) (9)
(9)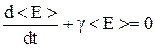 .
. (10) !Е0 із (6)!
(10) !Е0 із (6)!


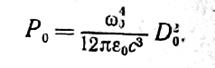
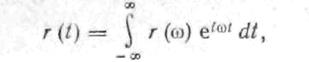 (14)
(14)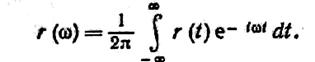 (15)
(15)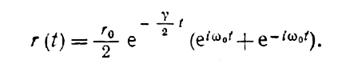
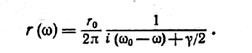
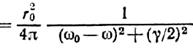 , (16)
, (16)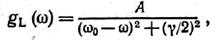 (17)
(17)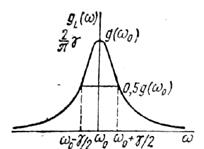 Вона має максимум при ω = ω0, який з умови нормування рівний g((ω0)=2/πγ. На відстанях ω0- ω=± γ/2 спектральна щільність убуває в два рази.
Вона має максимум при ω = ω0, який з умови нормування рівний g((ω0)=2/πγ. На відстанях ω0- ω=± γ/2 спектральна щільність убуває в два рази. (18)
(18)

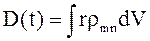
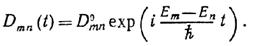 (19)
(19)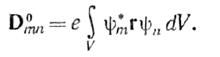 (20)
(20) ,
,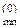 (множник 2 виникає пій переході від показової форми запису до тригонометричної).
(множник 2 виникає пій переході від показової форми запису до тригонометричної).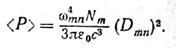 (22)
(22) маємо
маємо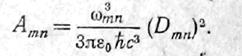
 .
.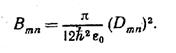 (23)
(23) , квантове сило змінюються від L+S до L-S через 1).
, квантове сило змінюються від L+S до L-S через 1).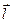



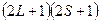 .
.


