
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Перевод чисел в системах счисленияСодержание книги
Поиск на нашем сайте
При переводе чисел из одной системы счисления в десятичную систему счисления используют полином представления числа в Q -итой системе счисления, а затем выполняют арифметические операции в десятичной системе счисления, например:
Например: перевод числа шестнадцатеричной системы af 416 в десятичную систему счисления:
При обратном переводе чисел рассмотрим отдельно два случая перевода: целые и дробные числа. 4.1 Перевод целых чисел из Р -итой системы счисления в Q -ичную. В соответствии с представлением целого числа в системе Р по основанию в системе Q имеем:
Разделим правую и левую часть на Q в результате получим новую целую часть и дробную часть (остаток):
Проделав тоже самое, но уже с новым целым числом Пример: перевод число 9810 десятичной системы счислений в двоичную.
Остаток отображает число в двоичной системе счисления, начиная с младшего двоичного разряда: Проверка осуществляется выполнением обратной операции:
Перевод дробной части Любое число меньше 1 можно представить полиномом следующего вида:
Для определения его разрядов в Q -й системе счисления необходимо число Пример: перевод десятичной дроби 0,62510 из десятичной системы счисления в двоичную.
Таким образом, двоичное число имеет вид 0,10102 Выполним проверку перевода по следующему выражению:
Лекция 4 Основы элементной базы цифровых автоматов 4.1 Логические элементы 4.2 Основы построения логических элементов 4.3 Элементы интегральных схем Логические элементы Основные логические элементы: И, ИЛИ, НЕ, И-НЕ, ИЛИ-НЕ, а также триггер. С помощью этих схем можно реализовать любую логическую функцию, описывающую работу устройств компьютера. Обычно у них бывают от двух до восьми входов и один или два выхода. Входные и выходные сигналы, соответствующие двум логическим состояниям в логических элементах – 1 и 0 – имеют один из двух установленных уровней напряжения. Например, +3 В и 0 В. Высокий уровень обычно соответствует значению «истина» («1»), а низкий – значению «ложь» («0»). Каждый логический элемент имеет свое условное обозначение, которое выражает его логическую функцию. Работу логических элементов описывают с помощью таблиц истинности. Схема И. Эта схема реализует конъюнкцию (умножение) двух или более логических значений. Условное обозначение на структурных схемах схемы И с двумя входами представлено на рисунке 4.1. Таблица истинности
Рисунок 4.1 – Условное обозначение и таблица истинности схемы И Единица на выходе схемы И будет тогда и только тогда, когда на всех входах будут единицы. Когда хотя бы на одном входе будет ноль, на выходе также будет ноль. Связь между выходом z этой схемы и входами x и y описывается отношением: z = x∙y (читается как x и y). Операция конъюнкции на структурных схемах обозначается знаком & (читается как амперсэнд), являющимся сокращенной записью английского слова and. Схема ИЛИ. Эта схема реализует дизъюнкцию (сложение) двух или более логических значений. Когда хотя бы на одном входе схемы ИЛИ будет единица, на ее выходе также будет единица. Условное обозначение на структурных схемах схемы ИЛИ с двумя входами представлено на рисунке 4.2. Знак 1 на схеме соответствует обозначению, т. е. значение дизъюнкции равно единице, если сумма значений операндов больше или равна 1. Связь между выходом z этой схемы и входами х и у описывается соотношением: z = х ν у (читается как х или у) Таблица истинности
Рисунок 4.2 – Условное обозначение и таблица истинности схемы ИЛИ Схема НЕ. Схема НЕ (инвертор) реализует операцию отрицания. Связь между входом х этой схемы и выходом z можно записать соотношением z = Если на входе схемы 0, то на выходе 1. Когда на входе 1, на выходе 0. Условное обозначение инвертора представлено на рисунке 4.3. Таблица истинности
Рисунок 4.3 – Условное обозначение и таблица истинности схемы НЕ Схема И-НЕ. Схема состоит из элемента И и инвертора, и осуществляет отрицание результата схемы И. Связь между выходом z и входами x и y схемы записывается следующим образом: Таблица истинности
Рисунок 4.4 – Условное обозначение и таблица истинности схемы И-НЕ Схема ИЛИ-НЕ. Схема состоит из элемента ИЛИ и инвертора и осуществляет отрицание схемы ИЛИ. Связь между выходом z и входами x и y схемы записывается следующим образом: Таблица истинности
Рисунок 4.5 – Условное обозначение и таблица истинности схемы ИЛИ-НЕ Триггер — (от англ. trigger — защелка, спусковой крючок) электронное устройство с двумя устойчивыми состояниями равновесия, чередующимися под воздействием внешних сигналов, предназначенных для записи и хранения одного бита данных. Для обозначения схемы триггера в английском языке чаще употребляется термин flip-flop, что в переводе означает «хлопанье». В отличие от рассмотренных выше логических схем, триггеры — это логические устройства c памятью. Выходные сигналы триггеров в общем случае зависят не только от их входных сигналов, действующих в настоящий момент, но и от сигналов, действовавших на входы до этого Самый распространенный тип триггера- RS -триггер. Принципиальная схема RS -триггера содержит защелку (два элемента И-НЕ или ИЛИ-НЕ), а также два раздельных статических входа управления. Q - прямой выход триггера;
S - раздельный вход установки в единичное состояние (напряжение высокого уровня на прямом выходе Q); R - раздельный вход установки в нулевое состояние (напряжение низкого уровня на прямом выходе Q);
S Q __ R Таблица истинности триггера с прямым входом.
Рисунок 4.6 – Условное обозначение и таблица истинности триггера Как видно из рисунка 4.6, комбинация R = 1 и S = 1 является запрещенной. После нее состояние выходов триггера становится неопределенным. На выходе Q может установиться как состояние логического ноля, так и состояние логической единицы. Иногда режим работы триггера, при котором R = 1, а S = 0, называется режимом очистки, при R = 0, S = 1 – режимом записи, а при R = 0, S = 0 – режимом хранения, так как информация на выходе триггера в этом случае не изменяется. Поскольку один триггер может запомнить только один разряд двоичного кода, то для запоминания байта нужно восемь триггеров, для запоминания килобайта соответственно 8 × 210 = 8192 триггеров. Современные микросхемы памяти содержат миллионы триггеров.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 261; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.14.208 (0.01 с.) |



 .
. .
. , получим другой остаток
, получим другой остаток  и другое целое число, с которым продолжим выполнение предыдущих операций, пока в остатке не получится число
и другое целое число, с которым продолжим выполнение предыдущих операций, пока в остатке не получится число 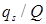 . Чтобы достичь этого, исходное число необходимо разделить на
. Чтобы достичь этого, исходное число необходимо разделить на 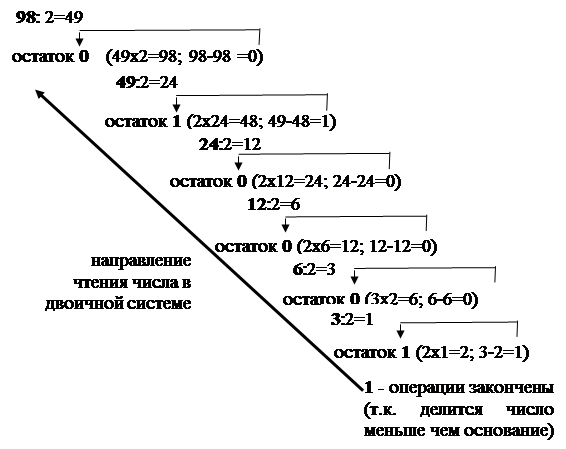


 умножать на Q, выделяя целую часть m -число раз пока не будет достигнута заданная точность.
умножать на Q, выделяя целую часть m -число раз пока не будет достигнута заданная точность. Решение:
Решение:
 0,
0,
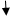
 0
0
 0,5 х2= 1,0; 1-1= 0
0,5 х2= 1,0; 1-1= 0



 , где
, где 

 , где
, где  читаются как “инверсия x или y ”. Условное обозначения на структурных схемах схемы И-НЕ с двумя входами представлено на рисунке 4.4.
читаются как “инверсия x или y ”. Условное обозначения на структурных схемах схемы И-НЕ с двумя входами представлено на рисунке 4.4.

 , где
, где  читается как “инверсия x или y”. Условное обозначение на структурных схемах схемы ИЛИ-НЕ с двумя входами представлено на рисунке 4.5.
читается как “инверсия x или y”. Условное обозначение на структурных схемах схемы ИЛИ-НЕ с двумя входами представлено на рисунке 4.5.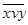

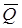 -инверсный выход триггера;
-инверсный выход триггера;




