
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Применение формулы Тейлора с остаточным членом в форме Лангранджа.Содержание книги
Поиск на нашем сайте Пусть функция f(x) – два раза дифференцируема в О(х0), тогда
уравнение касательной
Если |f’’(x)|£M "xÎO(x0) f(x)-n+1 – дифференцируема в О(х0)
f(x)=Tn(x)+Rn(x)§ в О(х0) n=1
n=2
- график парабола |f(x)-T1(x)|=|f’(x0)||x-x0| |f(x)-T2(x)|=[|f’’(x0)||x-x0|2]/2 T3(x)=ax3+bx2+cx+d – график кубическая парабола
Определение: Пусть функция f(x) – дифференцируема в точке х0, то она называется выпуклой (вогнутой) в верх в точке х0, если f(x)-yкас<0 в О(х0)
Определение: Пусть функция f(x) – дифференцируема в точке х0, то она называется выпуклой (вогнутой) вниз в точке х0, если f(x)-yкас>0 в О(х0)
Определение: Пусть функция f(x) – дифференцируема в точке х0, то она называется выпуклой (вогнутой) в верх (вниз) на интервале (a,b), если она выпукла в верх (вниз) в каждой точке этого интервала. Определение: (точки перегиба) Пусть функция f(x) диф- ференцируема в О°(х0) и непрерывна в О(х0). Точка х0 – называется точкой перегиба графика f(x), если при пере- ходе через точку меняется знак выпуклости.
Теорема: (о достаточном условии выпуклости функции). Пусть функция f(x) дважды дифференцируема в точке х0 и f’’(x0)<0 (f’’(x0)>0), тогда f(x) – выпукла вверх (вниз) в тоске х0. Доказательство: Напишем формулу Тейлора с остаточным членом в форме пеано:
Если х близко к х0, то знак квадрата скобки определяется знаком f(x0). Если f’’(x0)<0, то f(x)-yкас>0 в О°(х0). Если f’’(x0)>0, то f(x)-yкас>0 в О°(х0) Теорема: Путь функция f(x) непрерывна в О(х0) и дважды дифференцируема в О°(х0), причём f’(x) меняет знак при переходе через точку х0, тогда точка х0 – точка перегиба. Доказательство:
f’’(x) - +
x0 f’’(x)<0 в O°-(x0)Þ f(x) – выпукла вверх в О°-(х0) f’’(x)>0 в O°+(x0)Þ f(x) – выпукла вниз в О°+(х0) Следствие: Если f(x) дважды дифференцируемы в точке х0. Если точке х0 точка перегиба, то f’’(x0)=0 Путь точка х0 точка перегиба и существует f’’(x0)>0, тогда
то есть при переходе через точку х0 левая часть равенства f(x)-yкас не меняет знак. Аналогично получаем для f(x)>0 f’’(x0)=0 Замечание: Условие равенства f’’(x0)=0 необходимо, но недостаточно. Теорема: (о достаточном условие экстремума по второй производной) Пусть функция f(x) дважды дифференцируема в точке х0, тогда точка х0 точка максимума если f’’<0, точка х0 точка минимума если f’’(x0)>0. Доказательство:
При х достаточно большим и х0 знак в квадратных скобках совпадает со знаком f’’(x0)Þ f(x)-f(x0)>0 в О°(х0), если f’’(x0)>0 то есть f(x)>f(x0) в О°(х0)Þ х0 точка минимума, если f(x)-f(x0)<0 в О°(х0), и если f’’(x0)<0 то есть f(x)<f(x0) в О°(х0)Þ х0 точка максимума. Замечание: Если f’(x0)=0 и f’’(x0)=0, то нужны дополнительные исследования.
Лекция №17 Тема: Асимптоты. Полное исследование функции. Асимптоты. 1. Вертикальные 1.1 Пусть функция f(x) определена в 1.2 2. Наклонные асимптоты 2.1 Пусть функция f(x) определена в 2.2 Пусть функция f(x) определена в
|
||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 193; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

 f(x)=f(x0)+f’(x0)(x-x0)+[f’’(c)(x-x0)2]/2 где с лежит между х и х0
f(x)=f(x0)+f’(x0)(x-x0)+[f’’(c)(x-x0)2]/2 где с лежит между х и х0

 T1(x) – линейная функция
T1(x) – линейная функция
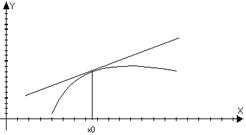 Выпуклость и вогнутость.
Выпуклость и вогнутость.


 (·) x
(·) x 

 , тогда прямая х=х0 называется правой вертикальной асимптотой для функции f(x)
, тогда прямая х=х0 называется правой вертикальной асимптотой для функции f(x) 
 Пусть функция f(x) определена в
Пусть функция f(x) определена в  , тогда прямая х=х0 называется левой вертикальной асимптотой для функции f(x)
, тогда прямая х=х0 называется левой вертикальной асимптотой для функции f(x) 

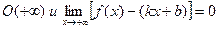 , тогда прямая y=kx+b называется правой наклонной асимптотой для функции f(x). (Если k=0, то говорят, что y=b – горизонтальная асимптота).
, тогда прямая y=kx+b называется правой наклонной асимптотой для функции f(x). (Если k=0, то говорят, что y=b – горизонтальная асимптота). 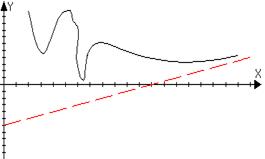

 , тогда прямая y=kx+b называется левой наклонной асимптотой для функции f(x).
, тогда прямая y=kx+b называется левой наклонной асимптотой для функции f(x).




