
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Модуль и основные неравенства.Содержание книги
Поиск на нашем сайте Матанализ Конспект лекций Введение Основные числовые множества. Окрестности. Модуль и основные неравенства. Функция. Монотонность. Ограниченность. Функции Ограниченные последовательности. Монотонные последовательности Пределы последовательности. Последовательности Бесконечно малые последовательности Свойства бесконечно малой последовательности. Теорема. Сумма бесконечно малой есть бесконечно малое. Теорема Произведение бесконечно малого есть бесконечно малое. Теорема о представление последовательности имеющий конечный предел. Теоремы о пределах числовых последовательностей. Теорема о пределе суммы: Теорема о произведение пределов: Теорема о пределе частного Бесконечно большие последовательности. Теорема (об ограниченной сходящейся последовательности) Теорема (о единстве предела сходящейся последовательности). Связь между бесконечно большими и бесконечно малыми величинами. Основные теоремы о существование предела последовательности. Бесконечно большие последовательности Определение под последовательности Предел функции. Замечательные пределы Первый замечательные пределы. Определение бесконечного предела и пределов при х®+¥. Односторонние пределы. Второй замечательный предел. Сравнение бесконечно больших и бесконечно малых. Шкала бесконечности. Степенные бесконечности. Показательные бесконечности. Основные эквивалентности. Асимптотические формулы Теорема(об ограниченности непрерывной функции в окрестности точки). Теорема:(о непрерывности сложной функции) Непрерывность некоторых функций. Точки разрыва» Классификация точек разрыва функции. Основные теоремы о непрерывных функциях. Теорема: (о сохранение знака непрерывной функции) Теорема Коши: (о нуле непрерывной функции) Теоремы Вейштрасса. Теорема: (Коши о промежуточных значениях) Теорема: (о существование и непрерывности обратной функции) «Без доказательства» Производная функции. Разность значений функций. Физический смысл производной. Геометрический смысл производной. Основные теоремы о производной. Теорема: (о произведение частного) Таблица производных Производные, дифференциал Дифференциал функции. Гиперболические функции. Линеаризация Геометрический смысл дифференциала функции и уравнение касательной. Линеаризация функции. Приближенные вычисления и оценка погрешности вычисления. Погрешности вычисления. Изучение поведения функции при помощи первой производной. Экстремумы функции. Теорема: (Ферма) (о необходимости условия экстремума дифференцируемой функции) «Экстремумы» Теорема (Ролля): Геометрический смысл. Теорема Лангранджа: Теорема: (о необходимых и достаточных условиях экстремума по первой производной) Производная функции высшего порядка. Производная функции высшего порядка. Теорема: (Коши – обобщение теоремы Лангранджа) Правила Лопиталя. Формулы Тейлора. Свойства многочлена Тейлора. Формула Тейлора с остаточным членом пеано. Пять основных разложений Формула Тейлора с остаточным членом в форме Лангранджа. Применение формулы Тейлора с остаточным членом в форме Лангранджа. Выпуклость и вогнутость. Теорема: (о достаточном условии выпуклости функции). Асимптоты. Полное исследование функции. Приближенные методы решения уравнения f(x)=0 Оценка скорости сходимости. Метод касательных (метод Ньютона) Формула Тейлора с остаточным членом в форме Лангранджа в точке xn Циклоида Параметрическая производная. Лекция №1 Тема: Введение Условные обозначения: : - так, что def – по определению Ì – включает ’’’ – [dnf(x)]/dxn=(d/dx)([dn-1f(x)]/dxn) Þ - следует, выполняется Û - тогда и только тогда " - любой $ - существует ] – пусть ! – единственный [x] – целая часть ~ - эквивалентно о - малое Все R представляют десятичной дробью. Все Q представляют конечной дробью, либо периодичной дробью. Все иррациональные числа представляют бесконечной десятичной дробью (не периодичной).
Рассмотрим числовую ось. Числовая ось – направленная прямая с отмеченной точкой и отмеченным масштабом.

0 – отвечает за ноль. Отрезок [0;1] отвечает за единицу Единица за единицу. Каждой точки х на числовой прямой отвечает некоторое действительное число. Если длинны отрезков [0; x ] из заданного масштаба соизмеримы, тогда числу х отвечает рациональное число. Если не соизмеримы, то иррациональны. Каждому R отвечает точка на числовой прямой и наоборот, каждой точке отвечает R. Основные числовые множества.
x
a b Обозначается [a;b] a£b Частный случай отрезка точка Или a£x£b – в виде неравенства.
х
a b Обозначается (a;b) или в виде неравенства a<x<b
x
a b x
a b Обозначается: [a;b) a£x£b (a;b] a<x£b Всё это числовые промежутки.
Замечание: один из концов (а или b) может быть символом ±¥.
x
b
x
b Вся числовая прямая – R =(-¥;+¥)
Окрестности. Определение: ε –окрестностью числа а называется множество чисел х удовлетворяющие неравенству
ε>0 а-ε а а+ε
Оε(а)={xÎ R:|x-a|<ε}
Проколотая ε окрестность – О°ε(а) это множество таких чисел включающих R, и отстаёт от точки на ε и не принадлежит а. О°ε(а)={xÎ R:0<|x-a|<ε}
а-ε а а+ε
Правая ε поло окрестность точки а: О+ε(а)={xÎ R:a£x<a+ε}
a a+ε Проколотая правая ε поло окрестность точки а: О°ε(а)={xÎ R:a<x<a+ε} Рисунок подобен предыдущему только с выколотой точкой а.
Левая ε поло окрестность точки а: O-ε(a)={xÎ R:a-ε<x£a}
a-ε a
Проколотая, левая ε поло окрестность точки а: О°-ε(а)={xÎ R:a-ε<x<a} Рисунок подобен предыдущему только с выколотой точкой а.
Лекция №3 Тема: Последовательности
Лекция №4 Тема: Бесконечно большие последовательности .
аn=(-1)n – не имеет предел. {bn}={1,1…} {an}={-1;1;-1;1…} – предел не существует.
Лекция №5 Следствие lim(1+1/n)n=e n®+¥ lim1/(1+1/n)n=(n/n+1)n=[1-1/(n+1)]n+1/ [1-1/(n+1)]=(1/e)/1=1/e n®+¥ lim[1/(1+1/n)n]=1/e n®+¥ lim(1+1/n)n=e n®+¥ Теорема Пусть последовательность an сходится, тогда "последовательности $ lim an=a "{ank} – гас и lim n®+¥ lim ank=0 n®+¥ Доказательство так как an – сходиться, то "ε>0 $N: "n>N Þ |an-a|<ε ank; nk>N то есть |ank-a|<ε Пример an=(-1)n – не имеет предела {a2n}={1,…,1,…,} {a2n-1}={-1,….,-1,…} имели бы тот же самый предел. Предел функции. Определение Пусть y=f(x) определена в O°(x0). Мы говорим, что функция f(x) имеет предел в при х®х0 если "ε>0 $ d>0 "x:0<|x-x0|<dÞ |f(x)-b|<ε lim f(x)=b x®x° Через окрестности это определение записывается следующим образом "ε>0 $d>0 "xÎ0°d(x0)Þf(x)Î0ε(b) Если lim f(x)=0, то f(x) наз бесконечно малой при x®x0. x®x° Замечание. Необходимо указать в каком именно процессе f(x) бесконечно малое. Надо указать к какому числу ® а. f(x)=x-1
1.x®1 lim(x-1)=0, то есть y=x-1 бесконечно малое при x®1 x®1
x®1 Пример f(x)=2x+1 x®1 Докажем lim(2x+1)=3 x®1 "ε>0 $d>0 "x:0<|x-1|<dÞ |(2x+1)-3|<ε |(2x+1)-3|<ε |x-1|<ε/2 x¹1 Положим d=ε/2 Теорема о бесконечно малом 1)a(x);b(x) – бесконечно малое x®x0 Þ a(x)+b(x) – бесконечно малое при x®x0 2)a(x);b(x) – бесконечно малое при x®x0 3)Если f(x) – ограниченна в O°(x0) и a(x) – бесконечно малое при x®x0, то f(x);a(x) – бесконечно малое при x®x0 Доказательство (3) Так как f(x) – ограниченна в O°(x0), то $ С>0: "xÎO°(x0)Þ|f(x)|£C; Так как a(x) – бесконечно малое при х®х0, то "ε>0 $d>0 "x: 0<|x-x0|<d Þ |a(x)|<ε "ε1>0 Положим ε=ε1/c $d>0 "x: 0<|x-x0|<dÞ |f(x)a(x)|=|f(x)||a(x)|<Cε=ε1Þ lim f(x)a(x)=0, то есть f(x)a(x) – бесконечно малое при x®x0 x®x° Лекция №6 Тема: Замечательные пределы Теорема f(x)>g(x) в O°(x0) и $ lim (f(x))=b и $ lim (g(x))=c. Тогда b³c x®x° x®x° Доказательство: Рассмотрим функцию g(x)=f(x)-g(x)>0 в O°(x0) Þ lim (g(x))= lim (f(x)) - lim (g(x))= b-c и в силу предыдущей x®x° x®x° x®x° теоремы b-c³0, то есть b³0 что и требовалось доказать.
Теорема f(x)£g(x)£g(x) " xÎO°(x0) и $ lim (f(x))=b и $ lim (g (x))=b. Þ lim (g (x))=b x®x° x®x° x®x° Доказательство: f(x)=b+a(x) g(x)=b+b(x) где a(x) и b(x) – бесконечно малые при х®х0 b+a(x)£g(x)£b+b(x) Так как a(х) и b(х) – бесконечно малые то "ε>0 $d1>0: " xÎO°d1(x0) Þ |a(x)|<ε $d2>0: " xÎO°d2(x0) Þ |b(x)|<ε Положим d=min{d1;d2}
|b(x)|<ε -ε<a(x)<ε -ε<b(x)<ε b-ε<b+a(x)£g(x)£b+b(x)<b+ε -ε<g(x)-b<ε |g(x)-b|<ε " xÎO°d(x0) " ε>0 $ d=min{d1;d2} Þ |g(x)-b|<ε "xÎO°d(x0) то есть lim (g (x))=b x®x° Определение f(x) определена в O°+(x0) lim (f (x))=b Û "ε>0 $d>0: " xÎO°+d(x0)Þf(x)ÎOε(b) x0<x<x0+d x®x°+0
Определение f(x) определена в O°-(x0) lim (f (x))=b Û "ε>0 $d>0: " xÎO°-d(x0)Þf(x)ÎOε(b) x0-d<x<x0d x®x°-0
Теорема Пусть f(x) определена в O°(x0) Для того чтобы существо- вал предел $ lim(f(x))=b Û $ lim(f(x))=lim(f(x))=b x®x° x®x°+0 x®x°-0 Пусть $ lim(f(x))=b, то есть "ε>0 $d>0: " xÎO°d(x0)Þf(x)ÎOε(b) f(x)ÎOd(b) для " xÎO°+d(x0) и для " xÎO°-d x®x° " xÎO°-d(x0)Þ$ lim(f(x));lim(f(x))=b что и требовалось доказать. x®x°+0 x®x°-0 Лекция №7 Шкала бесконечности. Степенные бесконечности. xn=o(xm), 0<n<m при х®+¥. Из двух степенных бесконечностей сильнее та, у которой показатель степени больше. Докажем: xn=xm(xn/xm)=xm(1/x(m-n))=xmg(x) m-n>0 xmg(x)ºo(xm) Основные эквивалентности. ex-1 – бесконечно малое при х®0. lim (ex-1)/x=1, то есть ex-1 ~ x при x®0 x®0 1-cosx – бесконечно малое при х®0. lim (1-cos x)/(x2/2)=lim{2sin(2x/2)]/[x2/2]=lim [2(x/2)2]/[x2/2]=1, то есть
1-cos(x) ~ x2/2 при х®0 и (1+x)p-1 ~ px при х®0
Лекция №8 Лекция №9 Тема: «Точки разрыва»
1) Доказать, что lim [((1+x)p-1)/px]=1 x®0
lim [((1+x)p-1)/px]= x®0 Þ y®0 =lim ([ln(1+x)]/x)([(1+x)p-1]/[pln(1+x)]=lim ([ln(1+x)]/x)· x®0 (1+x)p=y+1 x®0 x®0 p[ln(1+x)]=ln(y+1)
·lim([(1+x)p-1]/[pln(1+x)]=lim y/[ln(y+1)]=1 что и требовалось доказать Þ (1+x)p-1~px при x®0 x®0 y®0 (1+x)p=1+px+o(x) при х®0 2) Доказать, что lim (ex-1)/x=1 x®0
lim (ex-1)/x= x®0 Þ y®0 =lim y/[ln(y+1)]=1 что и требовалось доказать Þ x®0 ex=y+1 y®0 x=ln(y+1)
ex-1~x при x®0 ex=1+x+o(x) при х®0 Лекция №10 Тема: «Коши, производные»
Теорема: (Коши о промежуточных значениях) Пусть функция y=f(x) непрерывна на отрезке [a,b] и на концах принимает значение разные значения. f(a)=A f(b)=B A¹B. Тогда "С лежащею между А и В, $ х0Î(a,b): f(x0)=C. Другими словами нет точек которые не являются значением отрезка.
Эта функция непрерывна на отрезке [a,b] g(a)=f(a)-c=A-C<0 по теореме Коши №1Þ[1] $ x0Î(a,b):g(x0), то естьf(x0)-C=0Þ f(x0)=c g(b)=f(b)-c=B-C>0 Замечание: Условие непрерывности нельзя отбросить
[c,d]Ì[A,B] [c,d)ÏE(f)
Теорема: (о существование и непрерывности обратной функции) «Без доказательства»
Х° Х Разность значений функций. ∆y=∆f(x0)=f(x)-f(x0)=f(x0+∆x)-f(x0) – называется приращением функции в точки х0. Через эти обозначения можно определить непрерывность функций: f(x) – неопределенна в точки х0, если она определена в O(x0) и lim ∆y=0 ∆ x®0 lim[f(x)-f(x0)]=lim[f(x)-f(x0)]º0 lim[f(x)]=f(x0)] x-x°®0 x®x° x®x° Определение непрерывной функции в точки приращения: f(x) – неопределенна в точки х0, если она определена в O(x0) и lim ∆y=0 ∆ x®0
Определение: (производной функции) Пусть y=f(x) определена в О(х0) и $ lim[∆y/∆x]<¥, тогда этот предел называется производной функции f(x) в ∆х®0 точке х0. Обозначения: f’(x0), y’(x0), dy/dx, df(x0)/dx=df(x)/d(x) То есть f’(x0) по определению = lim[f(x)-f(x0)]/(x-x0)ºlim∆y/∆xºdy/dx ∆x®0 ∆x®0 Таблица производных y=sinx (sinx)’=lim[sin(x+∆x)-sinx]/∆x=lim[2sin(∆x/2)cos((2x+∆x)/2)]/∆x=lim[2(∆x/2)cos(x+(∆x/2))]/∆x=cosx ∆x®0 ∆x®0 (sinx)’=cosx
y=cos(x) (cos(x))’=lim[cos(x+∆x)-cos(x)]/∆x=lim[-2sin(∆x/2)sin((2x+∆x)/2)]/∆x=lim[-2(∆x/2)sin(x+(∆x/2))]/∆x=-sinx ∆x®0 ∆x®0 ∆x®0 (cos(x))’=-sinx
y=tg(x) (tg(x))’=(sin(x)/cos(x))’=[(sin(x))’cos(x)-(cos(x))’sin(x)]/cos2x=[cos2x+sin2x]/cos2x=1/cos2x (tg(x))’=1/cos2x
Лекция №11 Дифференциал функции. Определение: Пусть y=f(x) определена в некоторой О(х0) – она называется дифференцируемой в точке х0, если её приращение в этой точки представимо в виде: ∆y=∆f(x0)=A∆x+a(∆x)∆x)1 a(0)=0 A=const Определение: линейная ∆х часть приращение дифференцируемой функции называется дифференциалом функции в точке х0: dy=df(x0)ºA∆x Теорема: Если функция дифференцируема в точке х0 то A=f’(x0), то она имеет производную в этой точке, то A=f’(x0); наоборот если функция имеет производную в этой точке, то она дифференцируема в этой точке – называется дифференциалом. Доказательство:Пусть y=f(x) дифференцируема в точке х0, то есть в некоторой О(х0) справедливо равенство ∆f(x0)=A∆x+a(∆x)∆x1; a(0)=0. Поделим обе части этого равенства на ∆х и приведём к пределу при ∆х®0: lim(∆f(x0))/∆x=lim(A+a(x))=A. Этот предел существует, меньше ¥, тогда по определению этот предел есть ∆x®0 ∆x®0 производная. Доказательство: (в обратную сторону) Пусть в точке х0 $ f’(x0)(<¥) – это означает, что f(x) определена в некоторой О(х0) и $ lim(∆f(x0))/∆x=f’(x0)Þ по определению предела следует, что в некоторой О(х0) ∆x®0 (∆f(x0))/∆x=a(∆х)+f’(x0) при ∆х®0 Þ ∆f(x0)=f’(x0)+a(∆x)∆x, так как lima(∆x)=0, то в точке х0 y a(∆x) может ∆х®0 быть лишь устранимым разрывом. Устраним его, определим и доопределим: a(0)=0, тогда ∆f(x0)=f’(x0)∆x+a(∆x)∆x Þ A=f’(x0) из установленного соответствия получим выражения для дифференцируемой функции df(x0)=f’(x0)∆x Следствие: по определению полагают дифференциал независимой переменной равной её приращению dx=∆x (х - независимая переменная) df(x)=f’(x)dx f(x)=x – вычислим дифференциал f’(x)=1 df(x)=dx=f(x)∆x=1∆x Замечание: дифференциал функции зависит от двух переменных – от самой точки х и от ей приращения y=cosx x0=p/2 ∆x=p/180 y’=-sinx y’(p/2)=-sin(p/2)=-1 dy(p/2)=-1∆x=-1p/180=-p/180 Теорема: Пусть y=f(x) дифференцируема в точке х0, а z=g(y) дифференцируема в точке у0=f(x0), тогда сложная функция z=g(f(x) - дифференцируема в точке х0 и z’(x0)=g’(f)f’(x) Доказательство: (1) ∆z=g’(y0)∆y+a(∆y)∆y (2) ∆y=f(x0)∆x+b(∆x)∆x a(0)=0 b(0)=0 Подставим в первое равенство второе: ∆z=g’(y0)f(x0)∆x+g’(y0)b(∆x)∆x+a[f’(x0)+b(∆x)∆x][f’(x0)∆x+b(∆x0∆x] lim∆z/∆x=limg’(x0)f’(x0)+limg’(x0)b(∆x)+lim a(f’(x0)+b(∆x)∆x)[f’(x0)+b∆x] Þ z’(x0)=g’(y0)f’(x0) что и требовалось ∆x®0 ∆x®0 ∆x®0 ∆x®0 доказать. Теорема: Пусть функция y=f(x) возрастает (убывает) в О(х0) и дифференцируема в точке х0. Тогда обратная у ней функция x=g(y) дифференцируема в точки y0=f(x0), причём g’(y0)=1/f(x0)
∆у®0 монотонности функции и обратной = к ней следует ∆х¹0
∆y®0 ∆y®0 ∆у®0, то ∆х®0 и наоборот ∆x®0 ∆x®0
y=ax y’(x)=lim[ax+∆x-ax]/∆x=lim[ax(a∆x-1)]/∆x=lim[ax(e∆xlna-1)]/∆x=/∆x®0, то ∆xlna®0\=lim[ax∆xlna]/∆x=axlna ∆x®0 ∆x®0 ∆x®0 ∆x®0
y=lnx y’=lim[ln(x+∆x)-lnx]/∆x=lim[ln((x+∆x)/x)]/∆x=lim[ln(1+∆x/x)]/∆x=/∆x/x®0 при ∆x®0\=lim(∆x/x)/∆x=1/x ∆x®0 ∆x®0 ∆x®0 ∆x®0
y=arcsinx обратная функция x=siny xÎ[-1;1] yÎ[-p/2;p/2] (arcsinx)’|x=x0=1/(siny)’|y0=y=1/cosy|y0=y= yÎ[-p/2;p/2], cosy³0 cosy>0, если yÎ[-p/2;p/2] то есть x¹±1 =1/Ö(1-sin2y)|y=y0=1/Ö(1-(sinarccosx)2)|x=x0=1/Ö(1-x02) (arcsinx)’=1/Ö(1-x2)
y=acrcosx, обратная x=cosy xÎ[-1;1] yÎ[0;p] (arcosx)’=1/(cosy)’|y=y0=1/-siny|y=y0=-1/Ö(1-cos2y)|y=y0=-1/Ö(1-(cosarccosy)2)|x=x0=-1/Ö(1-x02) (arcosx)’=-1/Ö(1-x2)
y=arctgx обратная функция x=tgy yÎ(-p/2;p/2) (arctgy)’=1/(tgy)’=cos2y= / 1+tg2y=1/cos2y \ =1/(1+x2) (arctgy)’=1/(1+x2)
Гиперболические функции. chx=(ex+e-x)/2 shx=(ex-e-x)/2 chx2-shx2=1 chx2+shx2=ch2x ch(-x)=chx sh(-x)=-shx
Chx shx
(chx)’=sh(x) (shx)’=ch(x) (thx)=1
Лекция №12 Тема: «Линеаризация»
Геометрический смысл дифференциала функции и уравнение касательной.
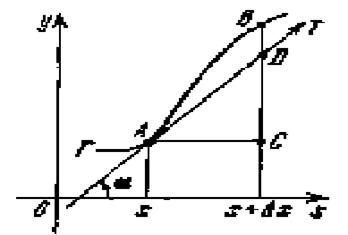
f’(x0)=tga уравнение прямой: Y=kx+b y0=f(x0)=kx0+b k-угловой коэффициент прямой k=tga=f’(x0) Y=f(x0)+f(x0)-f’(x0)x0 b=f(x0)-kx0 Y=f(x)+f’(x0)(x-x0)
∆f(x0)=f’(x0)∆x+a(∆x)∆x при ∆х®0 Þ в некоторой O(x0) f(x0)=f’(x0)+f’(x0)∆x+a(∆x)∆x при ∆х®0 Y1=f(x0)+f’(x0)(x-x0)a=f’(x0)+f’(x0)∆x df(x0)=f’(x0)∆x Геометрический смысл дифференциала: df(x0) – это приращение ординаты при движение по касательной проведённой к графику функции в точки (х0;f(x0). Замечание: Часто говорят о касательной проведённой в точке х0.
Линеаризация функции. Определение: Замена функции в окрестности данной точки линейной функции называется линеаризацией функции, точнее в О(х0) заменяется отрезком касательной в точке х0.
Если в равенстве (*) отбросить правую часть, то мы получим приближённое равенство: f(x)»f(x0)+f’(x0)(x-x0), x»x0 Y=f(x0)+f’(x0)(x-x0) – уравнение касательной в точке х0 Формула получена из определения дифференциала в точке х0 функции f(x)=f(x0)+f(x0)∆x+o∆x при ∆х®0 – называется критерием дифференциальности функции в точке х0. Погрешности вычисления. f(x)-f(x0)=df(x0)+o(x-x0) при х®х0 ∆f(x0)»df(x0), x»x0 ∆1=|∆f(x0)|»|df(x0) f(x)=10x в точке х0=4, если |∆х|=0,001 х=4±0,001 104±|∆|=104±|23| f’(x)=10xln10; f’(4)=104ln10=23000; ln10»2,2 |∆|»23000·0,001=23 Изучение поведения функции при помощи первой производной. Слева от М0 tg a>0; Справа от М0 tg a<0 tga f’(x)>0 слева от М0 tga f’(x)<0 справа от М0
Теорема: Пусть y=f(x) дифференцируема " xÎ(a,b) и f’(x)>0 (f’(x)<0), тогда f(x) возрастает (убывает) на (а,b)
"x1,x2Î(a,b) x1<x2 Надо доказать: f(x1)<f(x2) Применим теорему Лангранджа на отрезке (х1,x2)Теорема. f(x2)-f(x1)=f’(c)(x2-x1) где cÎ(x1,x2) f(x2)-f(x1)>0 Þ f(x2)>f(x1) Экстремумы функции.
f(x)<f(x1) b и О°d1(х1) анологично для точки х2 f(x)>f(x1) b и О°d2(х1). Значенгие функции в точке М1, М3 и М5 – max; M2 и М4 – min – такие точки назавыются точкками экстремума или точками локального max и min. Определение: (точки экстремума) Пусть функия f(x) определена в некоторой О(х0) и f(x)>f(x0) в О°(х0) или f(x)<f(x0) в этом случае точка х0 – называется точкой локального max (min).
f(x)£f(x1) в Оd1(х1) f(x)³f(x2) в Оd2(х2) говорят, что точки х1 и х2 точки не строгого локального экстремума.
Теорема: (Ферма) (о необходимости условия экстремума дифференцируемой функции) Пусть y=f(x) дифференцируема в точки х0 и точка х0 – точка экстремума, тогда f(x0)=0 Доказательсто: Заметим, что х0 точка экстремума, то в её окрестности f(x) – f(x0) сохраняет знак. Запишем условие ∆f(x0)=f(x)-f(x0)(x-x0)+o(x-x0) f(x)-f(x0)=(x-x0)[f(x0)+a(x-x0)] то при х – достаточно близких к х0 знак выражения стоящего в квадратных скобках совпадает со знаком f’(x0)¹0 (x-x0) – меняет знак при переходе черех точку х0 Þ f’(x0)=0
Лекция №13 Тема: «Экстремумы»
Замечание:
y=(x-1)3 y’=3(x-1)2 y’(1)=0 x0=1 xÎO°-d(1)Þf(x)<0 xÎO°+d(1)Þf(x)<0 x=1 – не точка экстремума.
Теорема (Ролля): Пусть функция y=f(x) непрерывна на отрезке [a,b] и дифференцируема на (a,b). Кроме того на концах интервала она принемает равные значения f(a)=f(b), тогда $ сÎ(a,b): f(c)=0 Доказательство: Така как функция непрерывна на отрезке [a,b], то по второй теореме Вейштрасса есть наибольшее и наименьшее значение (m,M), если m=M, то f(x)ºconst ("xÎ[a,b]) (const)’=0. Пусть m<M, тогда либо m, либо М отлична от значений на концах отрезка. Пусть например M¹f(a):$ c(a,b):f(c)=M, то есть точка с точка экстремума максимума следовательно по теореме Ферма f’(c)=0 Замечание: условие дифференцируемсти нельзя отбросить.
непрерывна на отрезке [a,b] Геометрический смысл.
f’(x)=0, то касательная || оси х. Теорема не утверждает, что это единственная точка.
Теорема Лангранджа: Пусть функция y=f(x) непрерывна на отрезке [a,b] и дифференцируема на отрезке (а,b), то $ сÎ(a,b): f(b)-f(a)=f(c)(b-a) Доказательство: F(x)=f(x)+lx где l - пока неизвестное число. F(x) – непрерывна на отрезке [a,b] как сумма непрерывной функции f(x) – дифференцируема на отрезке [a,b] как сумма дифференцируемой функции. Выберем число l, так чтобы на отрезке [a,b] F(x) принимало равное значение. F(a)=f(a)+la F(b)=f(b)+lb F(a)=F(b) Þ f(a)-f(b)=l(a-b) Þ l=[f(b)-f(a)]/[b-a] F(x) – удовлетворяет условию теоремы Роллера на отрезке [a,b] Þ $ cÎ(a,b):F’(c)=0, то есть F’(x)=f’(x)+l
То есть на кривой которая наклонена к оси х под таким же углом как и секущая [f(b)-f(a)]/[b-a]=tga=f(x) $ cÎ(a,b) Замечание: Часто точку с можно представить в нужном виде: с=х0+q∆х 0<(c-x0)/(x-x0)= q<1 c-x0=q(x-x0) c=x0+q(x-x0)1 f(x)-f(x0)=f’(x0+q∆x)(x-x0) 0<q<1 ∆f(x0)=f’(x0+q∆x)∆x Теорема: (о необходимых и достаточных условиях экстремума по первой производной) Пусть y=f(x) непрерывна на отрезке [a,b] и дифференцируема в О°(х0). Если f’(x) меняет знак при переходе через точку х0, то точка х0 – точка экстремума. Если меняет знак: с + на – то это точка максимума с – на + то это точка минимума Доказательство: " х1 Î О°-(х0) на [x1,x0]; $ c1Î(x1,x0) f(x0)-f(x1)=f’(c1)(x0-x1) Þ f(x0)>f(x1) "x1ÎO°-(x0) " х2 Î О°+(х0) на [x0,x2]; $ c2Î(x0,x2) f(x2)-f(x0)=f’(c2)(x2-x0) Þ f(x2)<f(x0) "x2ÎO°+(x0) f(x0)>f(x) "xÎO°(x0) Þ точка х точка максимума. Если в точке х0 существует производная то она обязательно равна 0 в силе теоремы Ферма. Но могут быть точки в которых f(x) существует, а f’(x) не существует. Принцип решения подобных задач: Условие: найти наибольшее и наименьшее значение функции не отрезке [a,b]. Ход решения: 1) Находим точки в которых производная либо равна 0 либо не существует f’(x)=0 или f’(x) 2) Вычисляем знак функции на концах отрезка и в этих точках f(a), f(b), f(x1)….f(xn) 3) Выбираем наибольшее и наименьшее m£f(x)<M Определение: точки в которых функция определена, а производная либо равняется нулю, либо не существует называют критическими точками. Лекция №14 Правила Лопиталя. Это правило в случае дифференцируемости функции позволяет избавляться от неопределённостей типа 0/0 или ¥/¥ при вычисление пределов. Теорема: Пусть функции f(x) и g(x) дифференцируемы в О(х0), g’(x0)¹0 в О°(х0), f(x0)=g(x0)=0 и $ lim f’(x)/g’(x)=k (конечный или бесконечный предел), тогда $ lim f(x)/g(x)=lim f’(x)/g’(x)=k x®x° x®x° x®x° Доказательство: lim f(x)/g(x)=lim [f(x)-f(x0)]/g(x)-g(x0)=lim f’(c(x))/g’(c(x))= | $ c=c(x) лежащая между х их0 если x®x° x®x° x®x° х®х0 то с®х0 | =lim f’(x)/g’(x)=k x®x° Замечание(1): f(x0)=g(x0)=0 требование можно заменить требованием lim f(x)=0, lim g(x)=0, то есть в т х0 f(x) и x®x° x®x° g(x) могут иметь устранимый разрыв, действительно достаточно переопределить или доопределить f(x) и g(x) по непрерывности, так чтобы f(x0)=g(x0)=0 Замечание(2): Если $ f’(x0) и g’(x0), g’(x0)¹0, то утверждение теоремы будет: lim f(x)/g(x)=lim f’(x)/g’(x)=lim [(x-x0)(f’(x0)+a(x-x0))]/ [(x-x0)(g’(x0)+b (x-x0))]=f’(x0)/g’(x0 | |||||||||||||
|
| Поделиться: |

 Отрезок: [/////////] x
Отрезок: [/////////] x ///////////////] x (-¥;b] или -¥<x£b
///////////////] x (-¥;b] или -¥<x£b a-ε<x<a+ε Û |x-a| Û (////·////) x Û Оε(а)
a-ε<x<a+ε Û |x-a| Û (////·////) x Û Оε(а) (////°////) x
(////°////) x · ///////) x
· ///////) x

 2.x®2 lim(x-1)=1, то есть y=x-1 не является бесконечно малой при x®2
2.x®2 lim(x-1)=1, то есть y=x-1 не является бесконечно малой при x®2 Тогда " xÎO°d(x0) Þ |a(x)|<ε
Тогда " xÎO°d(x0) Þ |a(x)|<ε

 Доказательство: A<B, "CÎ(A,B) g(x)=f(x)-C.
Доказательство: A<B, "CÎ(A,B) g(x)=f(x)-C.
 Пусть на множестве D задана непрерывная возрастающая или убывающая функция y=f(x). Тогда на множестве её значений Е определена обратная ей функция x=g(y), которая непрерывна и возрастает или убывает на множестве Е.
Пусть на множестве D задана непрерывная возрастающая или убывающая функция y=f(x). Тогда на множестве её значений Е определена обратная ей функция x=g(y), которая непрерывна и возрастает или убывает на множестве Е. Производная функции. ∆Х
Производная функции. ∆Х

 ∆x=x-x0 – называется приращением аргумента в т х0 Х
∆x=x-x0 – называется приращением аргумента в т х0 Х
 где sin(x)
где sin(x) (sin(x))’=cos(x)
(sin(x))’=cos(x)



 y’=axlna, частный случай y=ex Þ (ex)’=ex
y’=axlna, частный случай y=ex Þ (ex)’=ex y=x^2
y=x^2 y’=x^2 lnx
y’=x^2 lnx (lnx)’=1/x
(lnx)’=1/x y=logax=lnx/lnaÞ (logax)’=1/xlna
y=logax=lnx/lnaÞ (logax)’=1/xlna y=lgx
y=lgx

 (arcctgy)’=-1/(1+x2)
(arcctgy)’=-1/(1+x2) y=arcctgx
y=arcctgx y’=--1/ (1+x^2)
y’=--1/ (1+x^2)


 cthx=chx/shx
cthx=chx/shx thx=shx/chx
thx=shx/chx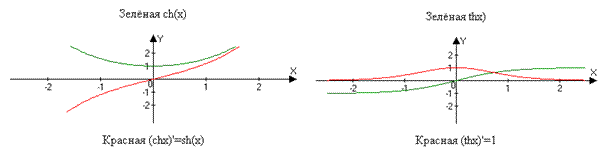

 (*) f(x)-Y=a(∆x)∆x-o(∆x)
(*) f(x)-Y=a(∆x)∆x-o(∆x)
 a(|x1 |x2)b
a(|x1 |x2)b Можно указать О(х1) в которой все значения функции
Можно указать О(х1) в которой все значения функции Замечание:
Замечание: Обратное утверждение неверно. Из-за того, что произведение в данной точки равно нулю, не следует, что это экстремум.
Обратное утверждение неверно. Из-за того, что произведение в данной точки равно нулю, не следует, что это экстремум.


 0=f’(c)+l Þ f’(c)=-l=[f(b)-f(a)]/[b-a]
0=f’(c)+l Þ f’(c)=-l=[f(b)-f(a)]/[b-a]


