
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Способи побудови нелінійних моделей.
Прогнозування за нелінійними моделями. За формулами, приведеними в попередній лекції, знаходимо межі інтервальних прогнозів для лінійної регресії, а потім шляхом зворотних перетворень (потенціювання) меж довірчих інтервалів прогнозу для лінійної регресії знаходять межі надійних інтервалів показникової регресії:
Тема 6. Криві зростання, їх властивості та методи побудови 1. Експоненційна функція. 2. Степенева функція. 3. Зворотні перетворення. 4. Квадратичні функції. 5. Логістична крива. 6. Крива Філіпа. 7. Крива Лафера.
Поняття про криві зростання Криві зростання описують різні тенденції економічних процесів, наприклад, життєвий цикл товару, процес нагромадження капіталу, маркетингові зусилля фірми тощо. Економічна практика вже накопичила певний досвід і певні типи кривих, які найчастіше використовуються в макро- та мікроекономічних дослідженнях. До таких кривих відносяться:
У загальному випадку однофакторну економетричну модель можна подати у вигляді y = f (x) + u, де f (x) - одна з функцій зростання, а u - випадкова величина. Як і у випадку з простою лінійною регресією, основне завдання полягає у розрахунку невідомих параметрів кривих зростання і подальшому аналізі обраної моделі. Оцінку невідомих параметрів проводять по-різному: експоненційні функції шляхом логарифмічних перетворень зводять до лінійної регресії, квадратичні функції зводять до багатофакторної регресії, для інших використовують ітеративні методи, метод трьох точок, метод Тейла тощо. Для тих функцій, які зводять до лінійної регресії, збігається вся методологія дослідження як і у випадку простої лінійної регресії. Експоненційна функція. Експоненційна функція може набирати різних чисельних еквівалентних форм:
Усі ці форми використовуються на практиці для опису різних економічних процесів. Наприклад, форму (3) найчастіше використовують у фінансах. В цьому разі r інтерпретується як норма річного відсотка. Розглянемо декілька прикладів застосування експоненційної функції у бізнесі та фінансах.
Приклад 1. Припустимо, що капітал С0 знаходиться у банку протягом t років із річним відсотком r. Він змінюється відповідно до функції (3), тобто через t років капітал дорівнюватиме:
З експоненційної форми легко отримати так зване правило 70, поширене в фінансових розрахунках. Правило 70 дає значення часу t, через яке змінна подвоїть своє значення відносно часу 0. Припустимо, що у початковий період часу ми маємо капітал С0, а в період часу t – капітал С t. Тоді подвоєння капіталу можна записати, переходячи від форми (3) до форми (2):
Отже, капітал подвоїться через Приклад 2. Приведення витрат до поточного часу. Порівнюючи різні інвестиційні проекти, ми повинні порівняти в першу чергу кошти, які на них витрачаються, та майбутні прибутки, які вони приноситимуть. Найпростіше це зробити, оцінюючи майбутні витрати та прибутки у вартості поточного року. Для ілюстрації розглянемо приклад. Заощаджуючи в банку А гривень у поточному році при ставці процента r, через t років ми отримаємо:
Відповідно В гривень, отриманих у t році при ставці відсотка r, у поточному році коштуватимуть:
Величина називається приведеними витратами В гривень через t років до поточного часу (при нормі відсотка r). Дискретною версією виразу З дискретною версією легше працювати, коли t – є цілим числом. Якщо t набуває неперервних значень, перевагу слід віддати виразам Приведені витрати можуть також визначатись для потоку платежів. При нормі відсотка r приведені витрати платежу В1, який ми мали б через t1 років, платежу В2 через t2 років,..., платежу Вn через tn років мають вигляд:
Приклад 3. Довічна рента. Довічна рента – це послідовність однакових платежів у рівновіддалені інтервали для певного проміжку часу. Приведені витрати ренти А, яка виплачується наприкінці кожного з N років при постійній нормі відсотка r, що нараховується неперервно, дорівнює:
Враховуючи, що вираз Якщо у виразі
За припущення, що ми будемо отримувати ренту довічно, тобто нескінченну кількість років
Якщо ж відсоток нараховується щорічно, приведену довічну ренту до поточного часу краще подавати у відомому вигляді:
Якщо ми скористаємось формулою
Якщо Взагалі експоненційні функції використовуються для опису швидко зростаючих або спадаючих економічних процесів. При цьому, якщо Параметр b можна інтерпретувати як коефіцієнт зростання у часі. Шляхом логарифмічного перетворення можна легко звести експоненційну криву у будь-якій формі до лінійної функції, що дає змогу розрахувати параметри МНК та використовувати подальший аналіз моделі, як і в разі простої лінійної регресії. Отже, маємо:
Степенева функція. Степенева функція є одною з найпоширеніших у практиці кривих зростання і описує дуже широкий спектр економічних процесів. Вона має такий вигляд: Розглядатимемо випадок, коли
Рис. Вигляд степеневої функції, коли β – не ціле число, х ≥ 0.
Рис. Вигляд степеневої функції, коли β – ціле число.
Якщо параметр При побудові моделі основне питання полягає в тому, щоб розрахувати невідомі параметри мультиплікативної кривої. Степеневу криву, так само як і експоненційну, шляхом логарифмічного перетворення можна легко звести до лінійної функції, що дає змогу розраховувати параметри МНК. Зведення до лінійної:
Степенева функція використовується для опису різних економічних процесів: виробничої функції Кобба-Дугласа, кривих байдужості, а також попиту на товари різних категорій, як так звана крива Торнквіста та ін. Зворотні перетворення. Узагальнена обернена модель має вигляд:
Вона нелінійна за х, але лінійна за параметрами
Вибіркова обернена модель: Особливість моделі: коли х прямує до нескінченності, величина Вигляд даної моделі значною мірою залежить від знака параметрів b0 та b1 (рис.). Нахил моделі:
Рис. Обернена функція.
Рис. Крива Енгеля.
Інший, не менш важливий випадок використання зворотної кривої (рис.) – крива витрат Енгеля, яка пов’язує споживчі витрати на товари із загальними витратами або доходом. Критичний рівень доходу, нижчий від якого товар не буде куплено, «стелю» насичення, яку не можна збільшити (на рис. дорівнює Квадратичні функції. У загальному випадку квадратична функція має вигляд: Якщо фактор х інтегрувати як змінну часу t, то Якщо b2 > 0, b1 > 0 квадратична функція описує поліпшене зростання. Вершина розташована перед часом 0 (рис. а). Якщо b2 > 0, b1 < -2 tb2 Квадратична функція описує уповільнений спад (рис. б). Якщо b2 > 0, -2 tb2 < b1 < 0 маємо класичний випадок параболи на мінімум (рис. в). Якщо b2 < 0, b1 < 0 квадратична функція описує прискорений спад (рис. г). Якщо b2 < 0, b1 > -2 tb2 квадратична функція описує уповільнене зростання (рис. д). Якщо b2 < 0, 0 < b1 < -2 tb2 маємо класичний випадок параболи на максимум (рис. е).
Рис. Квадратична функція.
Шляхом елементарної заміни змінних, а саме:
Логістична крива. Ця функція є зворотною до модифікованої експоненти:
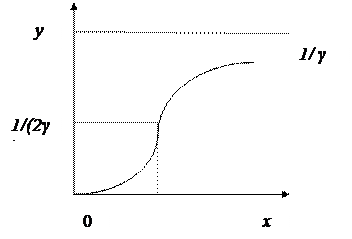
Логістична крива є типовою S – подібною кривою, у якої точка перетину припадає на середину стелі (рис.).
Рис. Логістична крива.
Властивості: 1. Асимптоти функції дорівнюють: 2. Перша похідна: 3. Друга похідна: Знак другої похідної збігається зі знаком виразу: Таким чином, логістична крива – S - подібна крива з «підлогою» 0 на початку і «стелею», що дорівнює
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 581; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.93.73 (0.101 с.) |
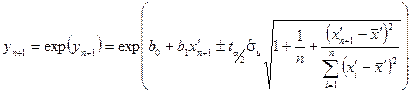








 >0; (1)
>0; (1) ,
,  , де b1 =
, де b1 = 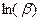 ; (2)
; (2)
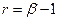 ; (3)
; (3) замінюємо на
замінюємо на  та
та  і
і  ; (4)
; (4) ,
,  замінюємо на
замінюємо на  і
і  ,
,  . (5)
. (5)

 років.
років.

 є відома формула
є відома формула  яку ми розглядали у першому прикладі, а зворотною до неї відповідно:
яку ми розглядали у першому прикладі, а зворотною до неї відповідно: 

 де PV – приведені витрати.
де PV – приведені витрати. його легко переписати у вигляді:
його легко переписати у вигляді: 
 припустити, що
припустити, що  тоді приведені витрати довічної ренти можна записати у вигляді:
тоді приведені витрати довічної ренти можна записати у вигляді:
 , цей вираз набуде вигляду:
, цей вираз набуде вигляду: за припущення, що
за припущення, що 

 і припустимо, що
і припустимо, що  то отримаємо:
то отримаємо:
 , то останній вираз остаточно набуде вигляду:
, то останній вираз остаточно набуде вигляду: 









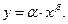
 , що є типовим для економічних процесів. Якщо значення параметра
, що є типовим для економічних процесів. Якщо значення параметра  - не ціле число, то розглядають випадок, коли
- не ціле число, то розглядають випадок, коли  . При цьому залежно від знака параметру
. При цьому залежно від знака параметру 


 , тоді
, тоді  , а графік функції симетричний відносно осі ординат (рис. а). Якщо
, а графік функції симетричний відносно осі ординат (рис. а). Якщо  , а графік функції симетричний відносно початку координат (рис. б).
, а графік функції симетричний відносно початку координат (рис. б). ,
, 
 .
. , і тому є лінійною регресійною моделлю. Позначивши
, і тому є лінійною регресійною моделлю. Позначивши , отримаємо
, отримаємо  .
.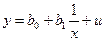 , де b0, b1 -невідомі параметри, які необхідно знайти, u – помилка.
, де b0, b1 -невідомі параметри, які необхідно знайти, u – помилка. прямує до граничного значення.
прямує до граничного значення. . Він є додатнім, коли b1 <0, і відємним b1 >0.
. Він є додатнім, коли b1 <0, і відємним b1 >0.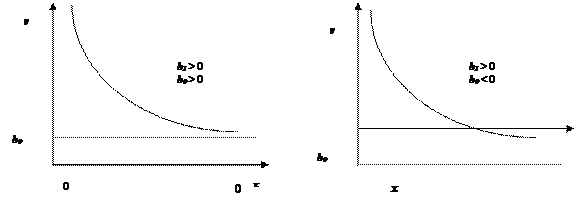
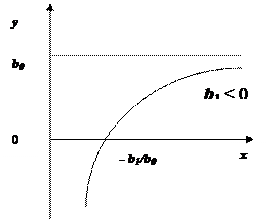
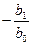 ), як би не зростав доход (на рис. це значення b0).
), як би не зростав доход (на рис. це значення b0).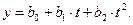 . Виходячи із значень b0, b1, b2 крива може відображати еволюцію – дуже різну на інтервалах часу
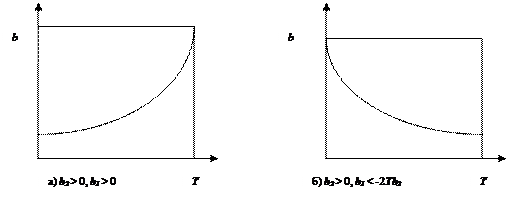
. Виходячи із значень b0, b1, b2 крива може відображати еволюцію – дуже різну на інтервалах часу 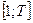 .
.

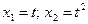 квадратичну функцію зводять до багатофакторної регресії, тому невідомі параметри розраховуються як для випадку багатофакторної регресії.
квадратичну функцію зводять до багатофакторної регресії, тому невідомі параметри розраховуються як для випадку багатофакторної регресії. .
.
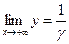 ;
; 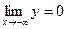 .
. коли
коли 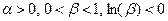 функція зростає.
функція зростає. .
. . Логістична крива має точку перетину, коли
. Логістична крива має точку перетину, коли 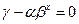 відповідно
відповідно  . У цій точці
. У цій точці 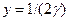 , тобто ордината точки перетину є серединою «стелі».
, тобто ордината точки перетину є серединою «стелі».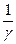 .
.


