
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
При їх підпорядкованому функціонуванніСодержание книги
Поиск на нашем сайте
У загальному випадку застосування готових пакетів прикладних програм у ГІС є доцільним при розв’язанні задач, що пов’язані з різноманітними трудомісткими розрахунками, не потребують відповіді в реальному часі і для яких існують добре зарекомендовані програмні засоби. До таких задач, зокрема, належать задачі проектування, календарного планування, статистичної обробки даних тощо. В разі ж комбінованого підходу до побудови ГІС, що працюють у режимі реального часу, доцільно розробити як інтелектуальну компоненту, так і алгоритмічні модулі з орієнтацією на їх спільне функціонування. До можливих застосувань таких систем можна зарахувати задачі диспетчирування виробництва, моніторингу, керування рухами робочих органів устаткування тощо. Варіанти умовної структури взаємодії компонентів ГІС при їх підпорядкованому функціонуванні показано на рис. 6.3, де рис. 6.3, а відповідає випадку, коли провідна компонента — алгоритмічний модуль, а рис. 6.3, б, в — коли провідною компонентою є EC; до того ж рис. 6.3, б є випадком подання знань у вигляді продукційних правил, а рис. 6.3, в — у вигляді фреймів. Найбільш природний варіант програмної реалізації звернення алгоритмічних процедур до EC (див. рис. 6.3, а) полягає у формуванні та застосуванні відповідних інтерфейсних функцій (функцій узгодження), аргументи яких передаються в EC для виконання виведення. У загальному випадку таке звернення може мати вигляд:
де Аналогічно може бути реалізована ініціалізація числових розрахунків EC. Зокрема ініціалізація їх EC продукційного типу досягається за допомогою правил, консеквентами яких служать оператори звернення (імена) до відповідних процедур, тобто загальний вигляд цих правил є таким:
Звернення до алгоритмічних модулів від інтелектуальних компонентів, які реалізовано на основі фреймового підходу, досягається використанням механізму приєднуваних процедур (див. п. 2.4), за допомогою яких визначаються необхідні програмні модулі. Виконання цих процедур здійснюється активізацією відповідних слотів фрейму. Розглянемо такий приклад. Гібридна інтелектуальна система (ГІС), що використовує фреймове подання знань, формує виробничі завдання в ГВС і розподіляє їх за модулями технологічного обладнання. Одним з етапів прийняття рішень є прогнозування їх можливих наслідків, яке виконується за допомогою імітаційного моделювання. Таким чином, EC реалізує провідну функцію, а IМ — підпорядковану. При цьому прогін моделі розглядається як приєднана процедура. Приклад можливої структури міжфреймових обмінів даними наведено на рис. 6.4. Значеннями більшої частини слотів фрейму «ФОРМУВАННЯ ЗАВДАНЬ» є приєднані процедури, що реалізують окремі етапи, пов’язані з таким формуванням. Процедура «ПРОГНОЗ» складається з формування функції «Запит»: перший запит стосується звернення до IM ГВС, другий — до модуля статистичної обробки даних. Службова функція «Запит» призначена для обміну повідомленнями між фреймами, її перший аргумент вказує ім’я фрейму-адресата, другий — ім’я слота.
Рис. 6.4. Приклад можливої структури міжфреймових обмінів даними Значеннями слотів фрейму «МОДЕЛЬ» є приєднані процедури, що реалізують моделювання окремих складових виробництва: ГВС, ЕРК, маніпуляторів тощо. Приєднана процедура «IМ ГВС» містить встановлення початкових значень параметрів конкретного ОМ (за допомогою службової функції «Запит»), а також прогін моделі. Фрейм «ГВС» містить слот «Об’єкт», значенням якого є покажчик фрейму конкретної ГВС, яка аналізується. В результаті виконання функції «Запит (ГВС; об’єкт)» формується покажчик фрейму «ГВС5», значення слотів якого є даними для прогону моделі. Спрощену структуру звернень показано на рис. 6.3, а штриховою лінією (відсутні можливі звернення фреймів для одержання випадкової інформації). Взаємодія EC і числових алгоритмів. Комбінований гібридний підхід є ефективним при спільному використанні EC, з одного боку, та методів математичного програмування, диференціального й інтегрального числень, розв’язання алгебраїчних, диференціальних та інтегральних рівнянь і їх систем, статистичної обробки даних — з іншого. При цьому EC може виконувати підготовчу і/або заключну функцію, а також брати участь у реалізації окремих кроків алгоритмів. Враховуючи особливе значення оптимізаційних задач у плануванні та управлінні, розглянемо їх докладніше. Зокрема, підготовчими функціями EC при розв’язанні задач оптимізації можуть бути: розпізнавання класу задач за видом цільової функції та обмежень; вибір методу розв’язання; зведення постановки задачі до стандартного вигляду, необхідного для застосування конкретної програмної реалізації методу; компонування алгоритму з готових бібліотечних модулів. На етапі оптимізації виконання процедур пошуку EC може використовуватись для: вихідної локалізації області пошуку; вибору початкової точки; вибору кроку; вибору напрямку пошуку; прогнозування положення екстремуму; пошуку множин Парето-оптимальних рішень тощо. При цьому застосування EC може бути виправдане в тих ситуаціях, коли ефективними є евристичні прийоми розв’язання важкоформалізованих ситуацій, що виникають у процесі пошуку EC, або коли область пошуку дуже значна, а розрахунок цільової функції потребує багато часу, або коли функція відклику має складну форму, розриви, стрибки, численні локальні екстремуми тощо. Прикладами правил на підготовчому етапі можуть бути такі:
Очевидно, для встановлення істинності відправлень таких правил, як і для реалізації приписок у висновках, повинні виконуватися відповідні процедури узгодження. Початкова локалізація області пошуку EC і вибір початкового наближення здійснюються на основі апріорної інформації про положення оптимуму, вплив на нього деяких факторів тощо. Наприклад, може бути відомо, що цільова функція монотонно збільшується по
Цій межі відповідає лінія АВ на рис. 6.5, а. При програмній реалізації в антецеденті правила замість символьного рядка «екстремум розташовується...» записується виклик відповідної процедури локалізації області пошуку.
Рис. 6.5. Поверхні відклику з локалізацією екстремумів на межі області пошуку ЕС ( а ) та ілюстрація набору початкового наближення ( б ) З накопиченої інформації може, наприклад, випливати, що зі збільшенням ЯКЩО зі зростанням І задано І відстань уздовж осі ТО для початкового наближення Згідно з цим правилом початковим наближенням по
де 9. Штучний інтелект у системах проектування 9.1. Методи та засоби відображення розв’язків оптимізаційних задач Метод повного перебирання варіантів. Для цього методу типовою є загальноінтелектуальна процедура: якщо інтелектуальна система потрапляє в нову ситуацію, вона намагається звести планування своїх цілеспрямованих дій до оптимізаційної задачі ― визначення множини Означення 9.1. Метод повного перебирання — це універсальний метод гарантованого розв’язання оптимізаційних задач за умови скінченності множини Метод евристичного пошуку. Оскільки для складних практичних ситуацій кількість варіантів перебирання надто велика (що потребує значних часових і машинних ресурсів), а також враховуючи ту обставину, що далеко не завжди слід шукати оптимальний розв’язок, часто обмежуються субоптимальним (наближеним до оптимального) або просто припустимим для поставленої мети розв’язком. У такому випадку необхідно виробити деяке правило (обмеження), яким перекривалося б повне перебирання варіантів пошуку при отриманні результату, який для більшості вхідних даних був би задовільним. Саме в цьому й полягає суть евристичного підходу. Означення 9.2. Евристичним пошуком називають процедуру систематизованого перебирання на основі послідовного аналізу можливих варіантів та оцінки їх наслідків [21] з такою схемою алгоритмічних кроків: · вибрати певну дію з області можливих; · здійснити дію; це приведе до зміни ситуації; · оцінити нову ситуацію; · якщо досягнуто успіху ― кінець; якщо ні ― почати з першого кроку. Одним з варіантів реалізації методу евристичного пошуку є стратегія послідовних поліпшень, яка полягає в тому, що за наявності певного наближення Стратегії організації пошуку вершин дерева перебирання. Найпоширенішими стратегіями організації пошуку необхідної вершини на дереві перебирання і шляху до неї є пошук у ширину і пошук у глибину. Означення 9.3. Стратегією пошуку в ширину називається організація такої процедури, яка передбачає проведення аналізу на кожному кроці породжень усіх вершин, що були проаналізовані на попередньому кроці, тобто паралельну перевірку всіх можливих альтернатив. Ця стратегія для наведеного прикладу 9.1 для булевого виразу з
Рис. 9.2. Стратегія з процедурою пошуку в ширину Означення 9.4. Стратегією пошуку у глибину називається організація такої процедури, якою передбачається першочерговий аналіз породжень тих вершин, що були проаналізовані останніми, тобто послідовну перевірку всіх альтернатив одна за одною, причому аналіз деякої альтернативи завершується тільки тоді, коли точно встановлюється, що вона приводить до успіху. У разі невдачі відбувається повернення на крок і розглядаються інші альтернативи. Ілюстрацією стратегії пошуку у глибину для умов того ж прикладу слугує аналогічне дерево перебирання з наведеною пунктирними стрілками послідовністю процедурного крокування (рис. 9.3).
Рис. 9.3. Стратегія з процедурою пошуку у глибину Стратегія пошуку у глибину набула більшого поширення на практиці і стала класичною загальноінтелектуалізованою процедурою в сучасних методиках планування цілеспрямованих дій. Простори станів і задач. Методики реалізації цілеспрямованих дій при організації пошуків розв’язків поділяються на два класи: планування в просторі станів і планування в просторі задач [42]. При плануванні в просторі станів заданим вважається набір станів (ситуацій) і відомі дії, які може здійснювати система і які визначають перехід від одного стану до іншого в процесі розв’язання задачі, тобто граф її станів. Означення 9.5. Граф станів задачі ― це орієнтований граф, вершини якого відповідають можливим станам об’єкта дослідження, а дуги ― методам переходу від стану до стану. Дуги можуть бути поіменованими мітками з інтерпретацією вартості або довжини відповідного переходу, і тоді загальний шлях від початкового стану до цільового визначає витрати на його реалізацію; при цьому типовою є вимога оптимізації цього розв’язку за певним (так званим енергетичним) критерієм. Фактично задача зводиться до пошуку в графі, основними машинними способами завдання якого є матриця інцидентності, матриця суміжності та списки суміжності. Планування у просторі задач передбачає декомпозицію початкової задачі на підзадачі доти, поки не буде досягнуто зведення до елементарних задач, для яких є готові алгоритми розв’язання. Якщо ж для деякої задачі готового алгоритму не існує, а її подальша декомпозиція неможлива, таку задачу вважають нерозв’язною. Для планування у просторі задач традиційно використовується формалізм І–АБО-графів. Означення 9.6. І–АБО - графом називається орієнтований граф, вершини якого відповідають задачам, а дуги ― відношенням між задачами, причому між дугами вводяться відношення «І» та «АБО». Будь-який І–АБО-граф можна звести до певної нормальної форми, в якій з будь-якої вершини виходять або тільки «І»-дуги, або тільки «АБО»-дуги. Означення 9.7. «І»-вершиною називається вершина, з якої виходять лише «І»-дуги; «АБО»-вершиною є вершина із виключно «АБО»-дугами. Означення 9.8. Початковою вершиною І–АБО-графа є вершина, з якої розпочинаються цілеспрямовані дії щодо розв’язання задачі. Означення 9.9. Вершина є розв’язною, якщо задача, що відповідає цій вершині, має розв’язок. З урахуванням означення 9.9 метою пошуку, що реалізується на І–АБО-графі, є встановлення факту розв’язуваності початкової вершини. Оскільки процедурно розв’язання задачі на І–АБО-графах нагадує механізм виведення продукційної системи, можна стверджувати, що фактично такі графи є фрагментами послідовностей виведення з продукційних систем. На завершення можна навести таке рекурсивне правило для встановлення того, є дана вершина розв’язною чи ні:
· «АБО»-вершина розв’язна, якщо хоча 6 одне її породження є розв’язним.
Метод динамічного програмування. Цей метод ґрунтується на схемі послідовного перебирання варіантів з використанням процедур, які на основі побічних оцінок відхиляють всі ті допустимі розв’язки, серед яких не може бути оптимального, тобто відбувається стиснення множини конкурентоспроможних варіантів до одного або декількох обмежених, які й порівнюються. Означення 9.10. Динамічне програмування ― це такий алгоритмічний метод, який доцільно використовувати, коли розв’язання задачі можна звести до певної послідовності розв’язків. При такому підході на кожному кроці перевіряються всі можливі послідовності розв’язків і за рахунок вилучення тих послідовностей, які не можуть бути оптимальними, задача значно спрощується. В цьому й полягає принцип оптимальності. Тоді під динамічним програмуванням щерозуміють такий спосіб побудови алгоритмів, який можна застосувати тоді, коли розв’язання загальної задачі можна розбити на розв’язок її підзадач і отримувати розв’язок наступної задачі як суперпозицію попередніх розв’язків.
9.3. Методи пошуку розв’язання на прикладах задач планування Пошук у просторі станів. Розглянемо можливе подання задачі стосовно формування плану-графіка завантаження устаткування. Початковий його стан Якщо мета полягає лише у виконанні операцій, а часові критерії відсутні (це, мабуть, нереально для практики), то кожна термінальна вершина графа служить розв’язком. При накладенні обмежень типу директивних строків без використання будь-якої цільової функції розв’язання досягається «пошуком у глибину» або «пошуком у ширину» з перевіркою виконання обмежень у кожній новій вершині та із завершенням пошуку в першій термінальній вершині, що задовольняє обмеження. Очевидно, така схема розв’язання розглядуваної задачі є вкрай неефективною й може призвести до повного перебирання. Мало того, за наявності критерію оптимальності саме ця схема й призводить до повного перебирання, оскільки заздалегідь невідомо, яка з допустимих термінальних вершин виявиться кращою (адже множина цих вершин задається не в явному вигляді, а умовою). Отже, такий підхід у чистому вигляді не підходить для складних реальних застосувань.
Рис. 9.10. Частково впорядковані набори операцій Скорочення кількості варіантів оптимальних (або раціональних) розв’язків досягається використанням спеціальних оцінних функцій, евристичних правил, додаткових обмежуючих узгоджень. Так, в основі багатьох практичних методів лежить схема, що імітує послідовність подій у реальній системі (див. рис. 9.11). Ця схема реалізовує односпрямований рух уздовж тільки одного з шляхів графа G, які об’єднують початкову та термінальну вершини.
Рис. 9.11. Послідовність подій у реальній системі Справді, в цьому разі хоча й існують альтернативні варіанти в кожній з вершин, однак після прийняття рішення (вибору партії серед претендентів) повернення не здійснюються, а всі потенційно можливі наступні стани подій локалізуються розташованим нижче підграфом. При цьому оптимальний розв’язок не гарантується, оскільки він може розміщуватися поза цим підграфом. Як компенсація цього недоліку — простота реалізації, скорочення простору пошуку при прийнятних показниках одержуваного субоптимального розв’язку. Практично описана схема розв’язання наведеної задачі доцільна в алгоритмічному вигляді, а не засобами EC, хоча в спрощеному вигляді вона може моделюватися набором таких правил:
Очевидно основним кроком, який визначає ефективність пошуку в загальній схемі розв’язання задачі й у стратегіях розглянутого вище типу, с вибір чергового оператора (відповідно вибір кращого претендента в правилах (9.1)). Зміст цього кроку відрізняє одну стратегію пошуку від іншої. Зміст інших кроків (можливо, за винятком початкового завантаження) схожий. Тому нижче розглянемо приклади можливих правил саме щодо цього кроку (основного), тобто щодо вибору кращого претендента. Тоді за наявності тільки вимоги виконання завдання (без критерію оптимальності) можливі правила матимуть вигляд:
а за наявності критерію оптимальності — вигляд:
У подальшому для зручності опису наведених нижче прикладів загальні елементи в лівій частині правил (тобто умови «вибір кращого претендента» та «використовуються обмеження за...») упускатимемо. Спочатку розглянемо випадок наявності тільки вимоги виконання завдань. Як правило, в цьому разі фігурують директивні строки їх завершення і можуть використовуватися, наприклад, такі евристичні правила для визначення напрямку перебирання кращого претендента:
де Як оцінна може бути вибрана або функція
або функція
де або функція
і т. д. (припускається, що для кожної з цих функцій За наявності критерію оптимальності залежно від його конкретного вигляду можуть застосовуватися такі евристичні правила, а також їх комбінації:
У наведених прикладах з критерієм оптимальності як оцінні можна вводити, наприклад, такі функції:
Пошук в ієрархії просторів. В основі цього підходу лежить ієрархічне подання компонентів проблемної галузі, наприклад, планування. Ієрархія може утворюватись у межах: власне простору станів (планів); множини цілей; множини операторів і стратегій щодо формування плану. Це досягається як виділенням безпосередніх складових планування, так і формуванням рівнів абстракції, коли підпростір верхнього рівня є узагальненим, абстрагованим від деяких елементів подання підпростору нижнього рівня (рис. 9.12).
Рис. 9.12. Приклад низхідного уточнення виробничого плану Основним об’єктом зазначеного ієрархічного подання є план. У цьому разі підставою для виділення рівнів є різний ступінь урахування в ньому основних компонентів і параметрів виробничого процесу, а саме: · повне подання фрагмента плану (наприклад, транспортні операції явно наводяться в плані, зазначаються їх часові інтервали і технічні засоби для виконання); · непряме подання фрагмента (наприклад, транспортні операції та їх виконавці в плані не зазначаються, але тривалості виконання операцій враховуються в тривалостях обробки відповідних партій деталей); · ігнорування фрагмента (наприклад, коли посилання на пересування вантажів відсутні, а тривалості їх виконання не враховано). До основних фрагментів планування, що впливають на виділення рівнів, належать: переналагодження устаткування (його наявність, тривалості використання тощо); структури завдань (партія — набір носіїв — сукупність деталей тощо); транспортні операції (розглядались вище); склад ресурсів (однотипні групи устаткування із сумарною продуктивністю, окремі одиниці устаткування тощо). Схема розв’язання задачі будується на принципі низхідного уточнення (top-down refinement): план, одержуваний на більш високому рівні, послідовно деталізується на більш низьких рівнях. У загальному випадку прийняття рішень на різних рівнях планування може бути рознесено в часі. До того ж, окремі рівні можуть виконуватися на різних стадіях виробничого процесу. Так, формування плану в межах етапів 1-3 (див. рис. 9.12) здійснюється до запуску партій деталей на обробку, проте рішення, що деталізують план до рівня руху носіїв (етап 4 на рис. 9.12), приймаються в процесі диспетчеризування при виконанні завдання (тобто в режимі реального часу). На різних рівнях планування можуть використовуватися й різні моделі. Так, ефективним є підхід, коли на верхніх рівнях застосовується фреймовий граф (рис. 9.12) як пошук у просторі станів (для початкового групування партії деталей за верстатами, призначення початкових налагоджень тощо), тоді як детальний розклад формується на нижчих рівнях з використанням імітаційної моделі (ІМ). Принцип найменших завершень. Ідея цього принципу полягає у відкладанні розв’язування окремих задач до одержання додаткової інформації, яка може бути одержана в процесі розв’язування інших задач. У міру надходження такої інформації, яка сприяє прийняттю кращого рішення, розв’язуються відкладені задачі, тобто здійснюється чергування окремих розв’язків задач, яке супроводжується спрямованим інформаційним обміном — одержаними окремими розв’язками, даними тощо. Як правило, принцип найменших завершень застосовується при ієрархічному поданні простору пошуку, коли уточнення розв’язків, одержуваних на більш високих рівнях абстракції, відбувається після розв’язання окремих, більш деталізованих задач. Однак суть підходу залишається справедливою і щодо підзадач одного рівня. Більше того, змістову узагальненість за цим принципом можуть мати стратегії, що характеризуються суттєвим часовим розподілом етапів й умовами їх виконання. У галузі планування можна навести приклад, коли попередньо формується розклад, який закріплює партії деталей за окремими групами устаткування, а конкретне чергування носіїв (у межах партії деталей) і пункти призначення транспортного засобу визначаються вже в процесі диспетчеризування, тобто в режимі реального часу.
Приклад 9.4. Для ілюстрації принципу найменших завершень розглянемо такий спрощений приклад. Припустимо, що при виборі конкуруючих претендентів на обслуговування (партії деталей 1 і 2 на рис. 9.13, а) ресурсом А враховується, зокрема, як скоро до нього надійдуть наступні претенденти. Проте потенціальні претенденти (партії деталей 3 і 4) на момент прийняття рішення можуть бути ще не закріпленими за тими ресурсами, які відповідають першочерговим етапам їх ТМ, тобто за верстатом 8. До того ж, вони можуть конкурувати як між собою, так і з іншими партіями деталей.
Рис. 9.13. Урахування потенційних претендентів (розв’язання конфліктів при їх виборі): а — рівні обліку; б — тупикова ситуація У цьому разі призначення ресурсу (верстата) А може бути відкладене, а здійснюватиметься закріплення відповідних партій деталей за ресурсом (верстатом) В з подальшим поверненням до уточнення їх закріплення за ресурсом А. Проте оскільки вибір серед партій деталей 3 і 4 здійснюється за тим самим принципом, це може призвести до досить довгих ланцюжків очікування залежних підзадач, а в гіршому разі — до появи тупикових ситуацій (рис. 9.13, б). Тут вибір серед партій деталей 1 і 2 відкладено до закріплення партії деталей 3 або 4 за ресурсом В, що, у свою чергу, залежить від вибору партій деталей, що закріплюються за ресурсом А. Практично можуть виникати довші та складніші цикли залежності.
Щоб запобігти надмірному збільшенню кількості відкладених задач, може використовуватись обмеження ланцюжків очікування із застосуванням на кінцевих підзадачах інших критеріїв або мішаних стратегій вибору. Для розв’язання тупикових ситуацій, зокрема, використовуються рівноймовірнісний випадковий вибір, додаткові евристики, різні для кожної з підзадач критерії, а також вибір претендентів за заздалегідь призначеним пріоритетом. Зазначені підходи можуть комбінуватись або може застосовуватися випадковий вибір з імовірностями, які пропорційні відносним пріоритетам претендентів за схемою методу Монте-Карло та ін.
Приклад 9.5. Використання принципу найменших завершень у разі ієрархічного пошуку розглянемо на такому прикладі. Нехай верхній рівень (рис. 9.14) складання плану полягає у формуванні груп різних претендентів, які закріплюються за різними (чи різнотиповими) наборами ресурсів на певному часовому інтервалі, а на нижньому рівні розв’язуються конфлікти між конкуруючими претендентами (якщо такі залишаються після вибору на верхньому рівні з урахуванням конкретних значень часу), тобто власне формування розкладу запусків партій деталей.
Рис. 9.14. Урахування потенціальної конкуренції претендентів
При цьому в процесі формування груп партій деталей (верхній рівень) критерієм є зменшення їх конкуренції на подальших етапах обробки (тобто стратегія тут випливає з евристичного припущення про бажаність запуску в одночасну обробку тих партій деталей, які не створюють потенційних перешкод одна одній у подальшому). Так, згідно з рис. 9.14, на ресурси (верстати) А та В надходитимуть відповідно партії деталей 2, 3. Очевидно, початкове призначення груп претендентів для всіх ситуацій, що відрізняються ступенем обробки партій деталей, практично неможливе й недоцільне внаслідок дуже великої кількості його можливих варіантів. Звуження ж набору ситуацій, які аналізуються, на кожному наступному часовому інтервалі можливе лише після виділення конкретних значень моментів часу для інтервалу, що минув (тобто в результаті формування його розкладу). При цьому може статися, що зайнятість деякого ресурсу охоплює й наступний часовий інтервал і, таким чином, виключає цей ресурс із списку доступних. Зауважимо, що поняття часового інтервалу є досить умовним: йдеться не про попередній розподіл планового періоду на фіксовані проміжки, а скоріше йдеться про плаваючий (поточний) проміжок часу, до того ж не жорсткої тривалості, а такий, що займає деякий прийнятий допуск і підлягає аналізу через звільнення в ньому кількості (відносно великої) ресурсів. У такому разі формування плану полягає в чергуванні етапів формування груп претендентів з етапами деталізації розкладу в межах груп. За наявності претендентів з близькими параметрами група може формуватися із включенням до неї претендентів, які конкурують на цей ресурс, і тоді конфлікт розв’язуватиметься на нижньому рівні. В разі відсутності невизначеності, а також при повній узгодженості наступних конкуруючих етапів значення часового інтервалу може призначатись у межах етапів формування груп. Використання глибинних знань. Застосування цих знань при розв’язанні задач планування передбачає врахування основних змістових і причинних взаємозв’язків між компонентами (поняттями), що лежать в основі поняття «план», а також урахування основних принципів його формування та впливу можливих ситуацій на значення базових критеріїв.
Приклад 9.6. Розглянемо такий спрощений приклад. Маємо один верстат і кілька деталей-претендентів на їх обробку. Вибраним критерієм оптимальності є мінімум сумарного часу очікування. Використовуємо правило, яке називається SPT- впорядкуванням (Shortest Processing Time Sequencing):
Якщо ж деякі деталі потребують обов’язкового переналагодження устаткування, то це правило набуває вигляду:
Іноді ставиться вимога враховувати тривалість виконання транспортних операцій. Для цього необхідно заздалегідь зазначити в консеквенті всі можливі складові або деталізувати антецеденти та згрупувати правила за умовами їх виконання:
і т. д. Очевидно, в реальній ситуації розглянутий підхід потребуватиме суттєвого розширення БЗ, однак і це не дасть змоги передбачити всі можливі ситуації. Водночас, як це легко передбачити, праві частини наведених вище правил мають загальний зміст: вони лише від
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 299; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.011 с.) |


 параметри, значення яких використовуються як умови (посилання) при виведенні в EC;
параметри, значення яких використовуються як умови (посилання) при виведенні в EC;  керуючі параметри, що задають режими виведення (прямий або зворотний, стратегії вибору правил, покажчики наборів продукцій тощо);
керуючі параметри, що задають режими виведення (прямий або зворотний, стратегії вибору правил, покажчики наборів продукцій тощо); 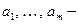 змінні, що містять допоміжну інформацію (ідентифікатори точок звернення тощо).
змінні, що містять допоміжну інформацію (ідентифікатори точок звернення тощо).
 при будь-яких фіксованих інших параметрах (рис. 6.5). У цьому разі можна застосувати таке правило:
при будь-яких фіксованих інших параметрах (рис. 6.5). У цьому разі можна застосувати таке правило:


 екстремум цільової функції монотонно зміщується в напрямку збільшення
екстремум цільової функції монотонно зміщується в напрямку збільшення 


 i
i  координати двох відомих точок екстремуму в уже дослідженій області.
координати двох відомих точок екстремуму в уже дослідженій області. припустимих розв’язків і цільової функції
припустимих розв’язків і цільової функції  і якщо це вдається, повним перебиранням отримується оптимальний розв’язок.
і якщо це вдається, повним перебиранням отримується оптимальний розв’язок. та обчислення на цьому елементі цільової функції
та обчислення на цьому елементі цільової функції 
 до розв’язку застосовується деяка процедура для переходу до іншого наближення
до розв’язку застосовується деяка процедура для переходу до іншого наближення  і якщо воно буде кращим за попереднє, продовжується генерація і випробування нового наближення і т. д. (нагадує процедури градієнтних підходів). Основні методи дослідження операцій ґрунтуються саме на цій стратегії. Проте слід зазначити, що евристичний пошук супроводжується експоненціальною складністю його реалізації.
і якщо воно буде кращим за попереднє, продовжується генерація і випробування нового наближення і т. д. (нагадує процедури градієнтних підходів). Основні методи дослідження операцій ґрунтуються саме на цій стратегії. Проте слід зазначити, що евристичний пошук супроводжується експоненціальною складністю його реалізації. ілюструється рис. 9.2.
ілюструється рис. 9.2.

 характеризується множиною завдань, які складаються з частково впорядкованих наборів операцій (рис. 9.10). Дія кожного оператора
характеризується множиною завдань, які складаються з частково впорядкованих наборів операцій (рис. 9.10). Дія кожного оператора  полягає в перенесенні найближчої операції одного з наборів у чергу до одного з відповідних верстатів. У кінцевому стані устаткування всі операції переміщуються в черзі. Процесу розв’язання такої задачі відповідає граф послідовності подій (рис. 9.11).
полягає в перенесенні найближчої операції одного з наборів у чергу до одного з відповідних верстатів. У кінцевому стані устаткування всі операції переміщуються в черзі. Процесу розв’язання такої задачі відповідає граф послідовності подій (рис. 9.11).

 (9.1)
(9.1)
 тривалість обслуговування партії деталей i на j *-й операції її технологічного маршруту (ТМ);
тривалість обслуговування партії деталей i на j *-й операції її технологічного маршруту (ТМ);  номери решти операцій;
номери решти операцій;  директивний строк обслуговування партії деталей і.
директивний строк обслуговування партії деталей і. де
де  а
а 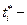 момент завершення останньої виконаної (на поточний момент) операції над і -ю партією деталей, причому
момент завершення останньої виконаної (на поточний момент) операції над і -ю партією деталей, причому

 вагові коефіцієнти,
вагові коефіцієнти, ,
,
 ).
).









