
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поняття та означення формальної системи знаньСодержание книги
Поиск на нашем сайте
В існуючій інформаційній технології використання ЕОМ переважають моделі, які мають синтаксичний характер. Наприклад, математичні моделі у вигляді систем диференціальних рівнянь можуть описувати процеси в об’єктах найрізноманітнішої природи. Той же універсалізм буде і при використанні оптимізаційних моделей лінійного чи нелінійного програмування тощо. Якщо математичну модель подати без коментарів, то неможливо сказати, який конкретно об’єкт або процес нею описується. Можна тільки зробити висновок про те, з якими класами об’єктів цю модель можна порівняти. Семантика відома лише спеціалістам, які формалізують процеси в тому чи іншому об’єкті. При цьому коментарі, що розкривають конкретні знання про об’єкт, а отже, й семантика формально-математичних моделей перебувають поза ЕОМ. Становлення нової інформаційної технології зумовлено тим, що в теорії ШІ розроблено логіко-лінгвістичні моделі, які дають змогу формалізувати конкретні змістовні знання про об’єкти керування (ОК) та процеси, що в них відбуваються, тобто ввести в ЕОМ логіко-лінгвістичні моделі поряд з математичними. Такі моделі — СС, продукційні системи, фрейми — іноді об’єднуються поняттям «програмно-апаратні засоби в системах із ШІ». Саме цим моделям зобов’язані своєю появою БЗ. Таким чином, нова інформаційна технологія відрізняється від існуючої насамперед тим, що за допомогою спеціальних формалізмі (логіко-лінгвістичних моделей) декларативні та процедурні знання подаються в електронній формі, завдяки чому розв’язування задач за допомогою ЕОМ відбувається більш ефективно. Етап перекладу умов задачі (ситуацій) з природної мови на формалізовану присутній в кожній науковій дисципліні. Фахівцям, які займаються дослідженням операцій, постійно доводиться описувати формальною мовою складні ситуації. Цей процес називається моделюванням. Система знань, подана формальною мовою, є формальною системою. Вона об’єднує суто абстрактні об’єкти (не пов’язані із зовнішнім світом), визначаючи правила оперування множиною символів у виключно синтаксичному трактуванні без урахування змістового осмислення (або семантики). Означення 1.9. Формальна система знань (ФСЗ) буде визначеною, якщо: 1) задано скінченний алфавіт (скінченну множину символів); 2) визначено процедуру побудови формул (або слів); 3) виділено деяку множину формул, які називаються аксіомами; 4) задано скінченну множину правил виведення, що дають змогу одержувати з деякої скінченної множини формул іншу множину формул, тобто Алфавіт, який заздалегідь вважається кінцевим, іноді називається словником. Спосіб подання формул (п. 2 означення 1.9 формальної системи знань) визначає конкретну синтаксичну конструкцію формул (граматику формул) — правильно побудовані послідовності символів. На відміну від цього в п. 4 означення 1.9 задаються дозволені правила виведення формул одна з одної. Означення 1.10. Формальне доведення (або просто доведення) визначається як скінченна послідовність формул Означення 1.11. Формула Якщо Вирізняють два типи правил виведення: 1) такі, що застосовуються до формул, які розглядаються як одне ціле (в цьому разі їх називають продукціями, або продукційними правилами); 2) такі, що можуть застосовуватись до будь-якої окремої частини формули, до того ж самі ці частини є формулами, які входять до складу ФСЗ (у цьому разі кажуть про правила переписування). Так, правило виведення
застосовується до формули як до цілого — це продукція (з двома анцетедентами, або посиланнями). На відміну від попереднього правило І продукція, і переписування мають тільки один напрямок виведення зліва направо. Підстановка полягає в заміщенні всіх входжень будь-якої змінної формулою з ФСЗ, що не містить цієї змінної. Правило підстановки придатне для використання в будь-якій ФСЗ. Незаміщувані символи називаються константами, а заміщувані — операторами. Оскільки ФСЗ завжди є моделлю якоїсь реальності (конкретної чи математичної), запроваджується поняття інтерпретації. Означення 1.12. Інтерпретація — це поширення вихідних положень будь-якої ФСЗ на реальний світ із наданням змістовності кожному символу цієї системи і встановленням взаємно однозначної відповідності між її символами та реальними об’єктами. Висновок 1.1. Теореми ФСЗ, будучи раз інтерпретованими, стають після цього твердженнями, і можна робити висновки щодо їх істинності або помилковості. Корисність і зручність ФСЗ полягає в їх абстрагуванні від конкретної реальності, завдяки чому одна й та сама ФСЗ може бути моделлю різних конкретних ситуацій. Але при цьому необхідно, щоб для цієї ФСЗ завжди існувала принаймні одна інтерпретація, в якій кожна теорема цієї системи була б істинною.
Способи подання знань Однією з ключових проблем створення ШІ є проблема подання і використання знань. В галузі ШІ поняття про знання сформувалося в ході досліджень із створення принципів і техніки роботи з великими обсягами даних і з побудовою даних ― БД. Ефективність БД багато в чому залежить від того, яким саме способом організуються, структуруються дані в пам’яті ЕОМ. До певного часу основну роль в цьому відігравали формальні характеристики даних: належність їх до деякої табличної рубрики, входження до однієї тематичної групи тощо. Проте ефективність БД можна істотно підвищити, якщо зв’язувати знання, що зберігаються, не за рахунок форм тих чи інших документів (таблиць, списків), а за рахунок тих відносин, які існують між фактами в об’єкті управління або в природному середовищі. І відносини ці мають бути не випадковими, ситуативними, а відображати істотні зв’язки об’єкта, його природу, тобто виникла необхідність відображати в БД знання про об’єкт. Такі БД стали називати інтелектуальними базами даних або базами (системами) знань. Ідеологія створення СЗ в основному пов’язана з формалізацією семантичної пам’яті, точніше, деяких її моделей, розроблених у когнітивній психології, а саме — семантичних сіток, фреймів тощо (насамперед сіток Петрі, які набули величезного значення для подання і перетворення знань щодо дискретно-подійних процесів, а також нейросіток у задачах класифікації, кластеризації, розпізнавання образів та нейро-фаззі-технологіях). Водночас розробляються СЗ на основі засобів логіко-символічних перетворень, що вивчаються в ШІ вже тривалий час і які мають розвинений відповідний математичний апарат. Форма подання знань суттєво впливає на характеристики та властивості системи, оскільки для маніпулювання будь-якими знаннями реального світу за допомогою ЕОМ необхідно здійснювати їх моделювання. При цьому враховують такі фактори, як однорідність подання та простота розуміння знань. Зазвичай при розгляді нескладних задач зупиняються на деякому середньому (компромісному) поданні знань. Розв’язання ж складних і великих задач потребує структурування й модульного подання знань. Кожна СЗ є математичною моделлю деякої галузі прикладного, неформалізованого знання. Система понять і відношень такої моделі відображає систему понять і відношень прикладного знання, а залежність, яка існує в моделі, апроксимує відповідну залежність у ньому. Створення СЗ передбачає розв’язання таких взаємопов’язаних проблем: · формалізація відповідної галузі прикладних знань. Це важке завдання, оскільки розв’язується вона вручну, потребує спільної роботи фахівців-прикладників і математиків і полягає у виборі або побудові концептуальної схеми моделі. Розробка методології всіх цих операцій і становить зміст першої проблеми — формалізації; · друга проблема — подання знань — пов’язана з розробкою формального апарату для опису способів їх фіксації в пам’яті ЕОМ; · розробка теорії обчислень та інших перетворень, що здійснюються в побудованих моделях, становить третю проблему — використання знань; · нарешті, четверта, технологічна проблема, розв’язанням якої займаються системні програмісти, — це проблема розробки засобів програмної підтримки моделей, тобто створення БЗ і систем управління ними. Основна увага в ШІ приділяється другій і третій з перерахованих проблем, причому провідна роль відводиться проблемі подання знань. На практиці її розв’язують разом з питаннями побудови концептуальних схем моделей подання знань, і багато хто вважає, що саме ця проблема і є основною для сучасного ШІ. Можна виділити два напрями, що склалися в дослідженнях ШІ, які спираються на принципи організації людської пам’яті (і моделювання виведення на підставі цих принципів), а також на логічне дослідження. Типовими моделями подання знань у першому напрямі є моделі, що ґрунтуються на використанні продукцій, фреймів і семантичних сіток. Результатом досліджень другого напряму стало створення моделі подання знань на основі логіки предикатів першого порядку. При цьому серйозна увага приділялась поданню знань і генерації виведення з використанням теоретичної послідовної системи, в основному математичної формалізації та логічної повноти. Навпаки, перший напрям ґрунтується на розумінні процесу усвідомлення чогось людиною, що потребує скоріше виразності, аніж математичної чіткості. У подальшому ці типові моделі подання знань (МПЗ) були доповнені спеціальними для конкретних випадків засобами, але класифікація моделей при цьому залишилася незмінною. Мова, що використовується для розроблення систем на основі цих моделей, називається мовою подання знань. Наступні розділи книги дають змогу повніше ознайомитися з особливостями типових МПЗ. Тут же дамо загальну їх характеристику. Логічна модель використовується для подання знань у системі логіки предикатів першого порядку та виведення висновків за допомогою силогізмів. У найпростішому випадку застосовуються логічні моделі подання фактів за допомогою предикатів з використанням атомарних формул: ОРІЄНТАЦІЯ (РОБОТ, ДЕТАЛЬ): робот орієнтує деталь; ПРОМИСЛОВИЙ РОБОТ (МП-9С): МП-9С — промисловий робот (ПР). Логічна модель може мати вигляд правильно побудованої формули (ППФ), що включає квантори існування ( ( Відмінними рисами логічних МПЗ (в тому числі й наведених вище) є єдність теоретичного обгрунтування та можливість реалізації системи формально точних означень і виведень. У моделі правил знання подаються сукупністю правил вигляду “ЯКЩО — ТО”. Системи баз знань (СБЗ), які ґрунтуються на цій моделі, називаються продукційними. Вони містять два діаметрально протилежні типи — з прямими (діагностичними) та зворотними (задачі проектування) виведеннями. Так, у продукційних системах із зворотними виведеннями за допомогою правил будується дерево І/АБО, що пов’язує в одне ціле факти та висновки, причому оцінка цього дерева на основі фактів, які є у БД, зводиться до виведення. Виведення можуть бути і двоспрямованими, коли спочатку оцінюється невеликий за обсягом масив одержаних даних і вибирається гіпотеза (приклад — прямі виведення), а потім запитуються дані, необхідні для прийняття рішень про придатність цієї гіпотези. На основі цих виведень можна реалізувати більш потужну та гнучку продукційну систему зі зворотним виведенням. Продукційні системи з прямими виведеннями містять три компоненти: 1) базу правил, що складається з набору продукцій (правил виведення); 2) БД, яка містить безліч фактів; 3) інтерпретатор для одержання виведення на підставі цих знань. Дві перші бази утворюють БЗ, а інтерпретатор відповідає МЛВ у вигляді циклу “розуміння — виконання”, причому в кожному циклі виконувана частина вибраного виведення оновлює БД. Як наслідок, зміст БД перетворюється від першорядного до цільового, тобто цільова функція (система) синтезується в БД. Незважаючи на простий цикл вибору та виконання (або оцінки) правил, необхідність періодичного порівнювання (ототожнювання) результатів прямого виведення в продукційних системах із зразком у БД призводить до того, що зі збільшенням кількості правил суттєво уповільнюється швидкість виведення. Отже, такі системи не здатні розв’язувати великомасштабні задачі. Інакше кажучи, збільшення обсягу знань, необхідність розв’язання складних задач, виконання гнучких виведень або підвищення швидкості виведення потребують структурування знань, тобто шляхом попереднього групування відповідних правил у деякому стані процесу виведення можна обмежити діапазон їх вибору. Структурування БД є ефективним і в тих випадках, коли об’єкти, для яких використовуються ці правила, мають ієрархічну структуру. Дедалі частіше МПЗ, які ґрунтуються на застосуванні зазначених правил, використовуються в комбінації з фреймовими моделями — систематизованими у вигляді єдиної теорії психологічними моделями пам’яті людини та її усвідомленням. Фрейм — це парадигма для подання знань з метою використання цих знань комп’ютером. Вперше фреймова модель була представлена Г. Мінським як спроба побудувати фреймову мережу, або парадигму, з метою досягнення більшого ефекту розуміння [71; 39 ]. З одного боку, Мінський намагався сконструювати базу даних, що містить енциклопедичні знання, а з другого — він хотів створити найбільш наочну описову базу, яка містила б інформацію в структурованій і впорядкованій формі. Ця структура дала б змогу вводити інформацію в комп’ютер в більш гнучкій формі, маючи доступ до того розділу, який потрібен у поточний момент. Мінський розробив таку схему, в якій інформація міститься в спеціальних чарунках — так званих фреймах, які з’єднані в мережу або систему фреймів. Приклад фреймової системи, що описує склад ПР, показано на рис. 1.5.
а
б Рис. 1.5. Структура ПР типу ПР 5-2 ( а ) та приклад фреймової системи, що описує його склад ( б )
Новий фрейм активізується з настанням нової ситуації. Відмітною його рисою є те, що він одночасно містить великий об’єм знань і водночас є достатньо гнучким для того, щоб його використати як окремий елемент БД, тобто одночасно підпорядковується як системному, так і ієрархічному принципу побудови знань. Термін “фрейм” був найбільш популярний у середині сімдесятих років, коли існувало багато його тлумачень, відмінних від інтерпретації Мінського. Фрейми використовуються в системах штучного інтелекту (наприклад, в ЕС) як одна з поширених форм подання знань. Важливим моментом у цій теорії є поняття фрейму — спеціальної структури даних для подання деякого концептуального об’єкта. Інформація про фрейм міститься в слоті — складовій фрейму. Всі фрейми взаємозв’язані й утворюють єдину фреймову систему, в якій органічно об’єднані декларативні та процедурні знання. Теорія фреймів стала поштовхом до розроблення кількох поширених тепер мов подання знань (FPL, FMS, KRL, KEE, KRINE, LOOPS та ін.) — середовища для розробок і досліджень у галузі інженерії знань. Цими мовами часто користуються фахівці цієї галузі. Зокрема, мовою FMS фреймова модель розглядається як ієрархічна структура даних із модульним поданням знань у вигляді певних форматів, які називаються фреймами. Кожний з них описує один концептуальний об’єкт, а конкретні властивості останнього та факту, що його стосується, відображають слоти — структурні елементи цього фрейму. Оскільки для концептуального подання об’єктів властива ієрархічність, цілісний образ знань будується у вигляді однієї фреймової системи, що має ієрархічну структуру. В слот можна підставляти різні дані; специфічною процедурою виведення у фреймі є приєднувальна процедура, що використовується як слот. Мова подання знань, які базуються на фреймовій моделі, особливо ефективна для структурного опису складних понять і розв’язання задач, в яких відповідно до ситуації бажано застосовувати різні способи виведення. Слід додати, що фреймову систему без механізму приєднувальних процедур (отже, і механізму пересилання повідомлень) часто використовують як БД продукційної системи. Більш наочними є мови, що спираються на сіткову модель подання знань. В основі такої моделі лежить ідея про те, що будь-які знання можна відобразити у вигляді сукупності об’єктів (понять) і зв’язків (взаємовідношення) між ними (див., наприклад, рис. 1.6).
Рис. 1.6. Приклад сіткового подання сукупності знань Рисунок супроводжується текстом, що містить деякі декларативні знання: “Зліва від верстата розташований приймальний бункер. Відстань до нього дорівнює двом метрам. Праворуч від верстата — бункер готової продукції. Він розташований поряд з верстатом. Робот переміщається паралельно верстату і бункерам на відстані 1 м”. Отже, на даному рисунку показано сіткове подання сукупності знань, зафіксованих у цьому об’єкті, у вигляді моделі семантичної сітки. Поняття і об’єкти, що зустрічаються в тексті, зображені у вигляді сітки, а взаємовідношення — у вигляді дуг, що зв’язують відповідні вершини. На рис. 1.7 зображено фрагмент семантичної сітки, що ілюструє речення “ПР типу Тур-10 протягом часу від t 1 до t 2 виконував операцію маніпулювання об’єктом типу ступінчастого вала”. На рисунку є дуги a, b, “ Виконавець ”, “ Об’єкт ”, “ Початок ” і “ Кінец ь”, причому дуги а та б означають відповідно “підмножину” й “елемент” і належать до ієрархічних понять.
Рис. 1.7. Фрагмент СС Нейронні сітки, або штучні нейронні сітки, відображають розвиток моделей, які з’явилися завдяки спробам імітування механізму мислення людини, що вже з огляду на цю обставину є формальними МПЗ. Для певних класів задач, що стосуються ШІ (насамперед розпізнавання, інтелектуального управління динамікою складних механічних систем тощо), нейросіткові моделі часто забезпечують більш ефективні рішення, ніж традиційні символьні підходи. Нейронна сітка є сукупністю нейронів і зв’язків між ними. Кожний нейрон виконує відносно просту функцію, але, будучи об’єднаними численними зв’язками в єдину структуру, всі вони разом утворюють систему, здатну розв’язувати складні задачі. Вирізняють два типи нейроподібних сіток. У сітках першого типу вузлами є формальні елементи, що описують окремі нейрони. В сітках другого типу вузлами є формальні елементи, що відповідають не окремим нейронам, а особливим сукупностям їх — нейронним ансамблям. Під нейронним ансамблем розуміють таку сукупність взаємозв’язаних нейронів, яка збуджується повністю при збудженні окремої її частини. Багато дослідників вважають, що саме нейронний ансамбль, а не окремий нейрон, і є функціональною одиницею мозку як системи, що забезпечує складну діяльність людини як живої істоти. Як об’єкт модельного опису нейронний ансамбль відрізняється від окремого нейрона двома основними особливостями. Одна з них полягає в тому, що початкове збудження ансамблю змінюється неперервно, а не за законом “так — ні”. Нейронний ансамбль можна описати як нелінійний перетворювач аналогової інформації, який задається набором певних статичних і динамічних характеристик. Інша особливість нейронного ансамблю полягає в тому, що він може бути поставлений у відповідність до деякої змістовної одиниці — поняття, образу тощо, тобто елементу, який бере участь у процесі розумової діяльності людини. Отже, нейроподібна сітка, вузли якої відповідають ансамблям, стає сіткою із семантикою, або семантичною сіткою (СС). Ця обставина значно змінює підхід до проблем синтезу сіток і змістової інтерпретації процесів, що в них відбуваються. У найзагальніших рисах результатом функціонування нейронної сітки є сигнал, який ідентифікує належність вхідного зображення до одного з кількох класів. Завдяки властивості навчатися сітка “зберігає” ці зображення у своїй “пам’яті” (тобто сітка здійснює категоризацію зображень). Елементарна складова сітки — нейрон — має кілька входів і один вихід. Структуру нейрона зображено на рис. 1.8, а (це Adeline — adaptive linear element [105; 201]).
Рис. 1.8. Структура нейрона ( а ) та варіанти нелінійностей в ньому ( б, в ) Елементи вхідного вектора множаться на вагові коефіцієнти Однією з найважливіших особливостей нейронної сітки є її здатність до навчання. В процесі навчання нейрона відбувається піднастроювання вагових коефіцієнтів таким чином, щоб він правильно класифікував максимальну кількість вхідних зображень. Звичайно, навчання нейронної сітки здійснюється значно складніше, ніж навчання одного нейрона. На практиці використовують різні евристичні підходи, що забезпечують наближене розв’язання задачі навчання нейронної сітки за прийнятний час. Одним з найвідоміших є метод зворотного поширення, який узагальнює на багатошарові нейронні сітки підхід, що лежить в основі методу найменших квадратів. У методі зворотного поширення на підставі мінімізації середньоквадратичних похибок між бажаним і фактичним виходами векторів розв’язку задачі послідовно під настроюються ваги зв’язків, Результати досліджень у галузі моделювання нейронних сіток значно розширили клас задач, що розв’язуються за допомогою нейроподібних сіток. Тепер до нього класу належать комбінаторні, оптимізаційні та інші задачі. Завдяки успіхам мікроелектроніки підготовлено технологічну базу для створення обчислювальних пристроїв, які здатні здійснювати паралельне оброблення інформації. Ці два фактори зумовили появу нейрокомп’ютерів — ЕОМ, архітектура яких найкраще пристосована до розв’язання задач моделювання нейронних сіток. За нашого часу нейрокомп’ютери створюються у вигляді компактних приставок до персональних ЕОМ, суттєво підвищуючи функціональні можливості їх. Ефективним засобом подання та моделювання дискретних процесів є сітки Петрі (СП). Їх основні властивості полягають у можливості відображення паралелізму, асинхронності, ієрархічності об’єктів, що подаються, більш простішими засобами. Тому використання сіток Петрі для дослідження ієрархічних дискретних систем, зокрема ГКІС, є найкращим. Сітка Петрі – причинно-наслідкова модель представлення подій, що виникають у процесі роботи дискретної системи. Процеси подаються як множина подій та умов. Події – це дії, послідовність настання яких керується станами системи. Стан системи визначається сукупністю умов, серед яких виділяють: предумови – пов’язані з фактом наступу події; постумови – пов’язані з фактом здійснення події. Таким чином, СП представляється сукупністю пов’язаних подій та умов, що виникають у описуваній системі. Для задавання СП найчастіше використовують такі способи, як теоретико-множинне визначення, графічне зображення та матричне подання. 1. Теоретико-множинне визначення СП. Формально сітка Петрі
де Необхідно зауважити, що перші чотири елементи визначають структуру системи, а останній елемент – динаміку поведінки системи, її початковий стан. Динаміка сітки пов’язана з рухом маркерів по позиціях у результаті спрацьовувань переходів, внаслідок чого маркуються нові позиції 2. Графічне зображення СП. Графічно СП – це дводольний орієнтований мультиграф, де: дводольність означає наявність двох типів вершин (позицій та переходів); орієнтованість означає, що всі дуги мають певний напрямок; мультиграф – дуги можуть мати кратність (вона позначається значенням над дугою або кількістю дуг). Графічне зображення пов’язане з теоретико-множинним визначенням таким чином (рис. 1.9): позиції
Рис. 1.9. Елементи сітки Петрі
3. Матричне подання СП. Матричне подання – це аналітичний спосіб представлення СП. У цьому випадку функції інциденцій та початкове маркування зображаються у вигляді матриць розміром
та вектором-стовпцем розміром
де 4. Правила роботи СП. Робота (функціонування) СП – послідовність спрацьовування переходів, внаслідок яких відбувається зміна маркувань позицій. Перехід
яка виконуються до умови здійснення модельованої цим переходом події – у кожній вхідній позиції переходу кількість маркерів не менша кратності дуг, що їх з’єднують (рис. 1.10).
а б Рис. 1.10. Виконання умови збудження переходу: Тоді умова спрацьовування збудженого переходу
тобто при спрацьовуванні збудженого переходу маркування
Рис. 1.11. Правило спрацьовування збудженого переходу Необхідно відмітити, що у випадку використання матричного способу подання СП умова збудження переходу
а умова спрацьовування:
де У будь-якому стані СП може існувати декілька одночасно збуджених переходів. Але послідовність їх спрацьовування не встановлена і може бути будь-якою без одночасного спрацьовування переходів. Тому в СП визначають декілька прийнятних послідовностей спрацьовувань переходів, породжуючих послідовності маркувань, що виникають. Це відображає паралелізм та недетермінізм СП. Таким чином, з функціонуванням сітки Петрі пов’язують дві послідовності: спрацьовуючих переходів та виникаючих (досяжних) маркувань. Ці послідовності є взаємозв’язаними. Два маркування
Рис. 1.12. Безпосередньо досяжне маркування Два маркування Таким чином, формально функціонування сітки подається: мовою СП
Рис. 1.13. Послідовність досяжних маркувань Ці послідовності об’єднуються у рамках єдиної моделі представлення роботи сітки – графа досяжності – орієнтованого графа, вершинами якого є маркування з множини
а б Рис. 1.14. Граф ( а ) і дерево ( б ) досяжності СП
|
||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 331; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.218.83 (0.012 с.) |

 де
де  формули формальної системи, а стрілка ® читається як «спричиняє» або «випливає».
формули формальної системи, а стрілка ® читається як «спричиняє» або «випливає». така, що кожна формула
така, що кожна формула  або є аксіомою, або за допомогою одного з правил виведення є вивідною з попередньої формули
або є аксіомою, або за допомогою одного з правил виведення є вивідною з попередньої формули  де
де 
 називається теоремою, якщо існує доведення, за яким вона є останньою, тобто
називається теоремою, якщо існує доведення, за яким вона є останньою, тобто  то ж будь-яка аксіома — це теорема.
то ж будь-яка аксіома — це теорема.

 має сенс при будь-якому вигляді x, що входить в правило як підвираз. Це вже правило переписування, і для позначення слова “спричинює” в даному разі використовується стрілка
має сенс при будь-якому вигляді x, що входить в правило як підвираз. Це вже правило переписування, і для позначення слова “спричинює” в даному разі використовується стрілка 
 ) і загальності (
) і загальності ( ): (
): ( ) [МАНІПУЛЯТОР
) [МАНІПУЛЯТОР 
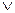 БАГАТОЛАНКОВИЙ
БАГАТОЛАНКОВИЙ  ) [ЗАХВАТ РОБОТА
) [ЗАХВАТ РОБОТА 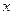 , ЗАХОПЛЕННЯ ТА УТРИМАННЯ)]: всі захвати ПР призначені для захоплення й утримання об’єктів роботизації.
, ЗАХОПЛЕННЯ ТА УТРИМАННЯ)]: всі захвати ПР призначені для захоплення й утримання об’єктів роботизації.




 ; зважені значення підсумовуються й надходять до входу порогового елемента, двійковий вихід якого є виходом нейрона. У загальному випадку для відтворення нелінійностей в нейроні можуть застосовуватися не тільки ступінчасті (рис. 1.8, б), а й похилі функції (рис. 1.8, в).
; зважені значення підсумовуються й надходять до входу порогового елемента, двійковий вихід якого є виходом нейрона. У загальному випадку для відтворення нелінійностей в нейроні можуть застосовуватися не тільки ступінчасті (рис. 1.8, б), а й похилі функції (рис. 1.8, в). може бути задана у вигляді п’яти елементів:
може бути задана у вигляді п’яти елементів:
 кінцева непорожня множина позицій (станів, місць);
кінцева непорожня множина позицій (станів, місць);  кінцева непорожня множина переходів (подій);
кінцева непорожня множина переходів (подій); 
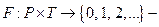 функція, що, визначивши передумови здійснення подій, призначає для кожного переходу вхідну множину позицій
функція, що, визначивши передумови здійснення подій, призначає для кожного переходу вхідну множину позицій 
 функція, що, визначивши постумови, призначає для кожного переходу вихідну множину позицій
функція, що, визначивши постумови, призначає для кожного переходу вихідну множину позицій 
 початкове маркування – кількість маркерів у позиції
початкове маркування – кількість маркерів у позиції 

 відображаються кругами; переходи
відображаються кругами; переходи 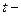 рисками; функції
рисками; функції  і
і  орієнтованими дугами, кількість або кратність яких визначається значенням функцій; маркування
орієнтованими дугами, кількість або кратність яких визначається значенням функцій; маркування  сітки відображається кількістю маркерів у позиціях.
сітки відображається кількістю маркерів у позиціях.





 може спрацьовувати, якщо він збуджений. Перехід
може спрацьовувати, якщо він збуджений. Перехід 

 має вигляд:
має вигляд:
 за правилом: з вхідних позицій переходу забирається певна кількість маркерів, яка визначається функцією
за правилом: з вхідних позицій переходу забирається певна кількість маркерів, яка визначається функцією  а вихідні позиції переходу отримують іншу кількість маркерів, яка визначається функцією
а вихідні позиції переходу отримують іншу кількість маркерів, яка визначається функцією 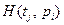 (рис. 1.11).
(рис. 1.11).


 вектор-стовпець розміром
вектор-стовпець розміром  у якого всі елементи дорівнюють 0, крім
у якого всі елементи дорівнюють 0, крім 
 спрацьовування якого переводить сітку з
спрацьовування якого переводить сітку з  тобто
тобто  (рис. 1.12).
(рис. 1.12).
 яка переводить сітку з
яка переводить сітку з  тобто виникає послідовність безпосередньо досяжних маркувань
тобто виникає послідовність безпосередньо досяжних маркувань  (рис. 1.13).
(рис. 1.13). множиною послідовностей спрацьовуючих переходів; множиною досяжності
множиною послідовностей спрацьовуючих переходів; множиною досяжності 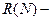 множиною маркувань, досяжних з початкового маркування.
множиною маркувань, досяжних з початкового маркування.
 а дугами – спрацьовуючі переходи з
а дугами – спрацьовуючі переходи з  (рис. 1.14, а). Граф з відсутніми циклами є деревом досяжності (рис. 1.14, б).
(рис. 1.14, а). Граф з відсутніми циклами є деревом досяжності (рис. 1.14, б).



