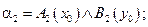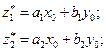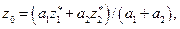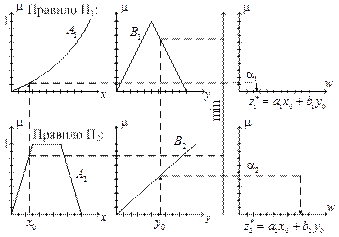Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поняття про недостовірні та нечіткі знанняСодержание книги
Поиск на нашем сайте Неповні та недостовірні знання. В розд. 1 та 2 розглядалися проблеми, пов’язані з використанням знань в ЕС та СПЗ. Розглянемо інші аспекти цієї проблеми. Неповні знання. Ця категорія знань свідчить про те, що для доведення або спростування певного твердження може не вистачати необхідної інформації. У багатьох системах логічного виведення прийнято постулат замкненості світу [21], що означає, що на запит про істинність деякого твердження відповіддю буде “ так ”тоді і тільки тоді, коли його можна довести; якщо ж довести це твердження неможливо, то відповіддю стане “ ні ”. Водночас “ неможливо довести через брак інформації ”(тобто неповноту знань)і “ доведено, що ні ” (тобто підтверджена неможливість використання знань через їх неповноту або хибність)— це зовсім не одне й те саме. Тому бажано, щоб в ЕС, якій доводиться мати справу з такими невизначеностями, формувався запит до користувача про факти, яких не вистачає. Недостовірність знань. На результат виконання деякого правила в продукційній СПЗ можуть впливати як випадкові чинники (об’єктивна невизначеність), так і такі, які залежать від невпевненості експерта в якомусь факті чи правилі виведення (суб’єктивна невизначеність). Таким чином, ненадійність знань і недостовірність наявних фактів можуть значною мірою вплинути на результати логічного виведення, які формуються інтелектуалізованою системою, і цей фактор обов’язково повинен враховуватися в процесі логічних побудов. Якщо ж просто відкидати факти і правила виведення, які викликають сумнів, то доведеться відмовитися від цінної інформації, яка була неточно подана або неправильно інтерпретована системою. Часто буває так, що експерт не зовсім упевнений в тому чи іншому факті, але, незважаючи на це, інформація залишається цінною і повинна бути включена в базу знань. Тому необхідно розвивати процедури, які дають змогу здійснювати логічні побудови при недостовірних даних, використовуючи ці процедури в ЕС. Нечіткість знань. На практиці часто доводиться мати справу з неточно визначеними або нечітко сформульованими поняттями ― лінгвістичними невизначеностями, такими, як “ багато ”, “ мало ”,“ сильно ”, “ слабо ”тощо. Враховуючи викладене, наведемо деякі означення. Означення 3.1. Висловлювання називається неточним, якщо його істинність або хибність не можуть бути встановлені однозначно, тобто твердження не є ані абсолютно достовірним, ані абсолютно хибним [42], Означення 3.2. Неточним виведенням називається логічне виведення в умовах неточності (недостовірності) знань. Модальне твердження. Неточне виведення традиційно розглядається як самостійний напрям, хоча неточне твердження можна було б інтерпретувати як частковий випадок модального твердження. Суть останнього полягає в тому, що воно оперує твердженнями, які дають оцінку іншим твердженням, або, інакше кажучи, є опосередкованими через інші твердження. Означення 3.3. Модальними логіками є логічні системи, які оперують модальними твердженнями. Як приклад наведемо такі модальні твердження, які можна занести в БЗ експертної системи: “ПР може захопити неправильно зорієнтовану деталь” (у таких випадках говорять про логіку можливого, або алетичну логіку) або “Система інформаційного забезпечення електроробокара визначає, що останній пройшов контрольну (реперну) точку відліку його місцерозташування в просторі” (це приклад так званих епістемічних логік). Неточне виведення слід відрізняти від роботи з нечіткими знаннями, хоча останні також формально підпадають під сформульоване вище визначення. 3.4. Нечітке логічне виведення Узагальнена постановка задачі нечіткого виведення. Механізм нечітких виведень, який використовується в різного роду експертних і керуючих системах, формується спеціалістами предметної галузі у вигляді сукупності нечітких предикатних правил виду:
де Отже, знання експерта Відношення
де «●» ― операція згортання (композиції). Операції композиції та імплікації в алгебрі нечітких множин можна реалізувати по-різному (з різними результатами), проте у будь-якому разі загальне логічне виведення здійснюється за такі чотири етапи [56; 76]: 1. Введення нечіткості (фаззіфікация) ― для визначення ступеня істинності кожної передумови кожного правила застосування функцій належності, визначених на вхідних змінних, до їх фактичних значень. 2. Логічне виведення ― застосування обчисленого значення істинності для передумов кожного правила до виведень кожного правила. Це приводить до однієї нечіткої множини, яка буде призначена кожною змінною виведення для кожного правила. Як правила логічного виведення зазвичай використовуються тільки операції 3. Композиція ― об’єднання разом усіх нечітких підмножин, призначених до кожної змінної виведення (в усіх правилах), для формування однієї нечіткої підмножини для всіх змінних виведення. При такому об’єднуванні зазвичай використовуються операції Властивості max-min- композиції. Операція
Крім того, для max-min -композиції виконується така важлива властивість:
Властивості max-* - композиції. Для max-min -композиції відношень
Зокрема, операція « 4. Зведення до чіткості (дефаззіфікація)― перетворення (при необхідності) нечіткого набору виведень до чіткої величини (числа). Існує багато методів зведення до чіткості, деякі з алгоритмів яких розглянуто далі. Але спочатку розглянемо приклад деякої системи, яка подається нечіткими правилами.
Приклад 3.4. Нехай деяка система задається нечіткими правилами вигляду (3.9):
де Процедура отримання логічного виведення ілюструється рис. 3.4. Припускається, що задано конкретні (чіткі) значення вхідних змінних: На першому етапі (фаззіфікація) на основі значень і, виходячи з функцій належності На другому етапі (логічне виведення) відбувається «відтинання» функцій належності виведень На третьому етапі (композиція) розглядаються функції належності, зрізані на попередньому етапі, і виконується їх об’єднання з використанням операції На четвертому етапі (дефаззіфікація) визначається, за необхідності, чітке значення вихідної змінної, що може реалізовуватися із застосуванням, наприклад, центроїдного методу: чітке значеннявихідної змінної визначається як центр ваги для кривої
Рис. 3.4. Ілюстрація процедури логічного виведення
Якщо проінтерпретувати наведені в прикладі 3.4 результати прикладом 3.2 з визначенням з виразу (3.15) чіткого значення Модифіковані алгоритми нечіткого виведення. Для розгляду найбільш уживаних модифікацій алгоритмів нечіткого виведення спростимо задачу, уважаючи, що базу знань утворюють тільки два нечітких правила виду:
де При цьому чітке значення Алгоритм Mamdani. Цей алгоритм відповідає вже розглянутому прикладу 3.4 і проілюстрований рис. 3.4. Математично для розглянутої ситуації його було подано чотирма етапами: · введення нечіткості (фаззіфікація) з визначенням ступеня істинності для передумов кожного правила: · логічне виведення із знаходженням рівнів «відтинання» для передумов кожного з правил (із застосуванням операції
де через «Ù» позначено операцію логічного мінімуму
· композиція з об’єднанням знайдених відтятих функцій із застосуванням операції
· зведення до чіткості з визначенням чіткого значення Алгоритм Tsukamoto. Для цього алгоритму вихідні посилання такі самі, що й для алгоритму Mamdani, але тут припускається, що функції
· нечітке виведення відбувається в два етапи. Спочатку визначаються рівні «відтинання»
знаходяться чіткі значення · зведення до чіткості значень змінної виведення (як зважене середнє
або для загального випадку (дискретний варіант центроїдного методу):
Приклад 3.5. Нехай задано (рис. 3.5): ступені істинності для передумов кожного правила (3.16)
відповідні рівні «відтинання»:
а також значення
Рис. 3.5. Ілюстрація до алгоритму Tsukamoto Тоді в результаті дефаззіфікації чітке значення змінної виведення, обчислене за виразом (3.17), має вигляд:
Алгоритм Sugeno. Цей алгоритм містить введення нечіткості (як в алгоритмі Mamdani) та нечітке виведення із знаходженням:
що ілюструється рис. 3.6.
Рис. 3.6. Ілюстрація до спрощеного алгоритму Sugeno
|
||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 251; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

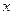 є
є  ТО
ТО  є
є 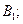 П2: ЯКЩО
П2: ЯКЩО  ТО
ТО 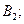 ...
П n: ЯКЩО
...
П n: ЯКЩО 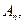 ТО
ТО 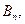
 вхідна змінна (ім’я відомих значень даних);
вхідна змінна (ім’я відомих значень даних);  змінна виходу (ім’я значення даних, яке буде обчислене);
змінна виходу (ім’я значення даних, яке буде обчислене); 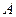 і
і 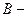 функції належності, визначені відповідно на
функції належності, визначені відповідно на 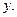
 відображує нечітке причинне відношення передумови і висновку, тому його називають нечітким відношенням і визначають як
відображує нечітке причинне відношення передумови і висновку, тому його називають нечітким відношенням і визначають як 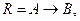 де «
де «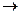 » ― нечітка імплікація.
» ― нечітка імплікація.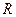 можна розглядати як нечітку підмножину прямого добутку
можна розглядати як нечітку підмножину прямого добутку 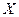 і виведень
і виведень  Тоді процес отримання нечіткого результату виведення
Тоді процес отримання нечіткого результату виведення 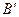 із застосуванням цього спостереження
із застосуванням цього спостереження 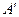 та знання
та знання 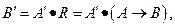
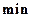 (МІНІМУМ) або
(МІНІМУМ) або  (ДОБУТОК). У логічному виведенні
(ДОБУТОК). У логічному виведенні 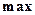 (МАКСИМУМ) або
(МАКСИМУМ) або  (СУМА). При композиції
(СУМА). При композиції 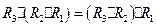 max-min -композиції асоціативна, тобто дистрибутивна відносно об’єднання, але недистрибутивна відносно перетину:
max-min -композиції асоціативна, тобто дистрибутивна відносно об’єднання, але недистрибутивна відносно перетину: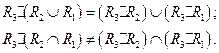
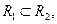 ТО
ТО 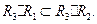
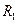 і
і 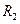 у виразі
у виразі  операцію «
операцію «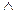 » можна замінити будь-якою іншою, для якої виконуються ті ж самі обмеження (наприклад, асоціативність, монотонність), що й для «
» можна замінити будь-якою іншою, для якої виконуються ті ж самі обмеження (наприклад, асоціативність, монотонність), що й для «
 є
є 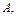 ТО
ТО 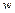 є
є  П2: ЯКЩО
П2: ЯКЩО 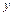 є
є  ТО
ТО  П3: ЯКЩО
П3: ЯКЩО 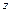 є
є 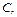 ТО
ТО 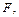
 імена вхідних змінних;
імена вхідних змінних; 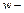 ім’я змінної виведення;
ім’я змінної виведення; 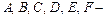 задані функції належності (наприклад, трикутної форми, див. розд. 2.6, рис. 2.18, д).
задані функції належності (наприклад, трикутної форми, див. розд. 2.6, рис. 2.18, д).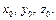
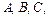 визначаються ступені істинності
визначаються ступені істинності 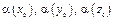 для передумов кожного з трьох наведених правил (3.14).
для передумов кожного з трьох наведених правил (3.14).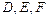 правил (3.14) на рівнях
правил (3.14) на рівнях 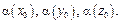
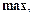 в результаті чого одержуємо комбіновану нечітку підмножину, яка подається функцією належності
в результаті чого одержуємо комбіновану нечітку підмножину, яка подається функцією належності 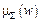 і відповідає логічному виведенню для вихідної змінної
і відповідає логічному виведенню для вихідної змінної 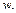

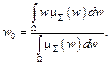

 для нормального утримання об’єкта в захватному пристрої, то це значення лежить у площині функції належності
для нормального утримання об’єкта в захватному пристрої, то це значення лежить у площині функції належності 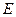 (рис. 3.4).
(рис. 3.4).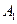 і
і 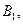 ТО
ТО 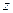 є
є 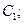 П2: ЯКЩО
П2: ЯКЩО 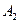 і
і 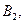 ТО
ТО 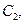
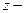 ім’я змінної виведення; A 1, A 2, B 1, B 2, C 1, C 2 — деякі задані функції належності.
ім’я змінної виведення; A 1, A 2, B 1, B 2, C 1, C 2 — деякі задані функції належності.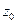 необхідно визначити на основі наведеної інформації і чітких знань
необхідно визначити на основі наведеної інформації і чітких знань 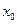 і
і 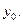
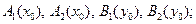
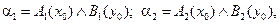
 Далі визначаються «відтяті» функції належності:
Далі визначаються «відтяті» функції належності:
 що дозволяє отримати підсумкову нечітку підмножину для змінної виходу з функцією належності:
що дозволяє отримати підсумкову нечітку підмножину для змінної виходу з функцією належності: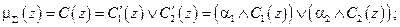
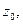 наприклад, центроїдним методом.
наприклад, центроїдним методом.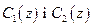 є монотонними. Тоді алгоритм Tsukamoto визначається такою послідовністю:
є монотонними. Тоді алгоритм Tsukamoto визначається такою послідовністю: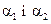 (як в алгоритмі Mamdani), а потім, розв’язуючи рівняння
(як в алгоритмі Mamdani), а потім, розв’язуючи рівняння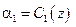 і
і 
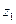 і
і 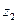 для кожного вихідного правила;
для кожного вихідного правила;
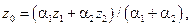
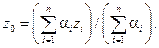
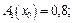
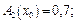

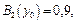
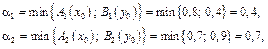
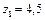 і
і 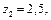 які знайдено в результаті розв’язання рівнянь
які знайдено в результаті розв’язання рівнянь 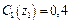 і
і 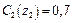 (див. рис. 3.5).
(див. рис. 3.5).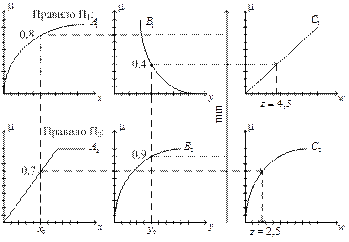
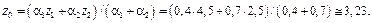
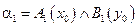 і
і