Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Переменные рабочего пространства.Содержание книги Поиск на нашем сайте Модуль 1 Векторная алгебра Арифметические вычисления. Упражение 1 Постановка задачи Знакомство с MATLAB. Изучение команд Упражнение 1.1 >> 1+2 ans = >> ans/4.5 ans = 0.6667 Упражнение 1.2 >> 1/2+2/3 ans = 1.1667
>> format rat 1/2+2/3 ans = 7/6 Упражнение 1.3 >> syms x >> f=(x+1)*(x-1) f = (x - 1)*(x + 1)
>> collect(f) ans = x^2 - 1 >> f=collect(f) f = x^2 – 1
Переменные рабочего пространства. >> x=1, y=2, z=3, t=4 x =
y =
z =
t =
>> whos x y z t Name Size Bytes Class Attributes
t 1x1 8 double x 1x1 8 double y 1x1 8 double z 1x1 8 double >> clear x >> whos y z t Name Size Bytes Class Attributes t 1x1 8 double y 1x1 8 double z 1x1 8 double
>> clear y z >> whos Name Size Bytes Class Attributes t 1x1 8 double Представление данных матрицами. Работа с массивами в MATLAB Упражнение 1.4 >> B=[1 3 -1]
B = 1 3 -1 >> B=[1, 3, -1] B = 1 3 -1 >> C=[-1;2.1] C = -1.0000 2.1000 >> A=[1 2 3 4;0 -1 -3 -2] A = 1 2 3 4 0 -1 -3 -2
>> n=3 n = >> m=[3] m = >> whos A B C n m Name Size Bytes Class Attributes
A 2x4 64 double B 1x3 24 double C 2x1 16 double m 1x1 8 double n 1x1 8 double
Упражнение 1.5. >> A(1,3) ans = >> A(5) ans =
Упражнение 1.6 Выполнить задания №1. Задать вектор-строку а. выполнить задания под буквами. А) a=[1 2 3 4 5] a = 1 2 3 4 5 B) >> a=[1,2,3,4,5]
a = 1 2 3 4 5 C) >> a=horzcat(1,2,3,4,5,6) a =
1 2 3 4 5 6 D) >> a=[1:2:3:4:5:6] a =
1 2 3 4 5 6 №2. Задать вектор-столбец b. Выполнить задание под буквами a) >> b ={ 1; 1.9; 2.8; 3.7}
b =
[ 1] [1.9000] [2.8000] [3.7000] b) >> b =[1: 1.9: 2.8: 3.7]' b = c) >> a1=a' a1 =
d) >> b2=b' b2 = 1 2 3 e) >> b3=vertcat(1,2,3,4,5,6) b3 =
Построение прямых на плоскости. Знакомство с функциями plot и line. Эти функции необходимы нам для построения векторов как в плоскости так и в пространстве Упражнение 1.7. Функция line >>line([0;-2],[0;-1]) >> grid on >> line([-2;0],[4;0]) Упражнение 1.8. >> line([0;0],[2;1]);
>> line([0;2],[2;0]);
>> line([0;2],[3;0]);
>> grid on
Упражнение 1. 10. >> line([0,0,-2;2,-2,0],[0,0,4;1,-1,0])
>> line([0,0,-2;2,-2,0],[0,0,4;1,-1,0])
>> grid on
Упражнение 1.11. >> line([0,0,0;2,2,3],[0,2,2;1,0,0])
>> grid on
Упражение 1.12.
>> subplot (2,2,1);
>>line([0;2],[0;1]);
>>subplot (2,2,2);
>>line([0;2],[2;0]);
>>subplot (2,2,3);
>>line([0;3],[2;0]);
>>subplot (2,2,4);
>>line([0,0,0;2,2,3],[0,2,2;1,0,0]);
Упражение 1.13.
>> subplot (2,2,1);
>>line([0;0],[2;1]);
>>subplot (2,2,2);
>>line([0;2],[2;0]);
>>subplot (2,2,3);
>>line([0;2],[3;0]);
>>subplot (2,2,4);
>> subplot (2,2,4);
>>line([0,0,0;2,2,3],[0,2,2;1,0,0]);
>>grid on;hold on;
>>plot(2,1,'>b','lineWidth',4);
>>plot(2,0,'<g','lineWidth',4);
>>plot(3,0,'vr','lineWidth',4);
Упражнение 1.14 >>line([0,0,-2;2,-2,0],[0,0,4;1,-1,0])
>> grid on,hold on
>> plot(2,1,'>b','lineWidth',4)
>> plot(-2,-1,'<g','lineWidth',4)
>> plot(0,0,'vr','lineWidth',4)
Упражнение 1.15
>> line([0,0,0;2,2,3],[0,2,2;1,0,0]) grid on,hold on plot(2,1,'>b','lineWidth',4) >> plot(2,0,'<g','lineWidth',4) >> plot(3,0,'<g','lineWidth',4) >> plot(3,0,'<r','lineWidth',4)
Занятие 2. Определители II и III порядков. Формулы Крамера. Определитель второго порядка На семинарных занятиях по линейной алгебре и начертательной геометрии мы знакомились с определителями ll и lll порядка. В данных упражнениях мы закрепим знания формул. Приложение определителя 2го Порядка к решению систем по формулам Крамера.
Проверка >>3*x1-5*x2 ans= 13 верно >>2*x1+7*x2 ans= 81 верно
>> B=[3 -4; 3 4] B = 3 -4 3 4 >> c=[-6; 18] c =
-6
>> d=B(1,1)*B(2,2)-B(2,1)*B(1,2) d =
>> d1=c(1)*B(2,2)-B(1,2)*c(2) d1 =
>> d2=B(1,1)*c(2)-B(2,1)*c(1) d2 =
>> x1=d1/d x1 = >> x2=d2/d x2 = Проверка >>3*x1-4*x2 ans= -6 Верно >>3*x1+4*x2 ans= 18 Верно
Упражнение 2.4 В данном упражнении мы должны вычислить определитель матрицы В по правилу Саррюса, а также разложить по первой строке, предварительно выполнив решение в тетради; выполнить проверку.
1.
>> A=[1,2,3; 4,5,6; 7,8,1] A = 1 2 3 4 5 6 7 8 1
>> detA=A(1,1)*A(2,2)*A(3,3)+A(1,2)*A(2,3)*A(3,1)+A(2,1)*A(3,2)*A(1,3)-A(1,3)*A(2,2)*A(3,1)-A(2,3)*A(3,2)*A(1,1)-A(2,1)*A(1,2)*A(3,3) detA = >> detA=A(1,1)*(A(2,2)*A(3,3)-A(2,3)*A(3,2))-A(1,2)*(A(2,1)*A(3,3)-A(2,3)*A(3,1))+A(1,3)*(A(2,1)*A(3,2)-A(2,2)*A(3,1)) detA = >> detA=det(A) detA = 24.0000 2. >> A=[3,4,-5; 8,7,-2; 2,-1,8] A = 3 4 -5 8 7 -2 2 -1 8 >> detA=A(1,1)*A(2,2)*A(3,3)+A(1,2)*A(2,3)*A(3,1)+A(2,1)*A(3,2)*A(1,3)-A(1,3)*A(2,2)*A(3,1)-A(2,3)*A(3,2)*A(1,1)-A(2,1)*A(1,2)*A(3,3) detA = >> detA=A(1,1)*(A(2,2)*A(3,3)-A(2,3)*A(3,2))-A(1,2)*(A(2,1)*A(3,3)-A(2,3)*A(3,1))+A(1,3)*(A(2,1)*A(3,2)-A(2,2)*A(3,1))
detA = >> detA=det(A) detA = 3. >> syms a b c x >> A=[a+x,x,x; x,b+x,x; x,x,c+x] A = [ a + x, x, x] [ x, b + x, x] [ x, x, c + x] >> detA=A(1,1)*A(2,2)*A(3,3)+A(1,2)*A(2,3)*A(3,1)+A(2,1)*A(3,2)*A(1,3)-A(1,3)*A(2,2)*A(3,1)-A(2,3)*A(3,2)*A(1,1)-A(2,1)*A(1,2)*A(3,3) detA = 2*x^3 - x^2*(b + x) - x^2*(c + x) - x^2*(a + x) + (a + x)*(b + x)*(c + x) Упростим >> simplify(detA) ans = a*b*c + a*b*x + a*c*x + b*c*x
>> detA=det(A) detA =
a*b*c + a*b*x + a*c*x + b*c*x >> detA=A(1,1)*(A(2,2)*A(3,3)-A(2,3)*A(3,2))-A(1,2)*(A(2,1)*A(3,3)-A(2,3)*A(3,1))+A(1,3)*(A(2,1)*A(3,2)-A(2,2)*A(3,1) detA = (a + x)*((b + x)*(c + x) - x^2) - x*(x*(b + x) - x^2) - x*(x*(c + x) - x^2) УПРОСТИМ >> simplify(detA) ans = a*b*c + a*b*x + a*c*x + b*c*x
>> detA=det(A) detA = a*b*c + a*b*x + a*c*x + b*c*x
4. >> A=[sin(a),cos(a),1; sin(b),cos(b),1; sin(c),cos(c),1 A = [ sin(a), cos(a), 1] [ sin(b), cos(b), 1] [ sin(c), cos(c), 1]
>> detA=A(1,1)*A(2,2)*A(3,3)+A(1,2)*A(2,3)*A(3,1)+A(2,1)*A(3,2)*A(1,3)-A(1,3)*A(2,2)*A(3,1)-A(2,3)*A(3,2)*A(1,1)-A(2,1)*A(1,2)*A(3,3) detA = cos(b)*sin(a) - cos(a)*sin(b) + cos(a)*sin(c) - cos(c)*sin(a) - cos(b)*sin(c) + cos(c)*sin(b) УПРОСТИМ >> simplify(detA) ans = sin(a - b) - sin(a - c) + sin(b - c)
>> detA=A(1,1)*(A(2,2)*A(3,3)-A(2,3)*A(3,2))-A(1,2)*(A(2,1)*A(3,3)-A(2,3)*A(3,1))+A(1,3)*(A(2,1)*A(3,2)-A(2,2)*A(3,1)) detA = sin(a)*(cos(b) - cos(c)) - cos(a)*(sin(b) - sin(c)) - cos(b)*sin(c) + cos(c)*sin(b) УПРОСТИМ >> simplify(detA) ans = sin(a - b) - sin(a - c) + sin(b - c)
>> detA=det(A) detA = cos(b)*sin(a) - cos(a)*sin(b) + cos(a)*sin(c) - cos(c)*sin(a) - cos(b)*sin(c) + cos(c)*sin(b) УПРОСТИМ >> simplify(detA) ans = sin(a - b) - sin(a - c) + sin(b - c)
Выполнив данное упражнение в тетради и затем рассчитав матрицы в программе MATLAB, я сверила и убедилась в том, что все решения сделанные мною в тетради верны. Упражнение 2.5 Номера из данного упражнение следует решить по формуле Крамера, затем выполнить проверку. Формула Крамера: Пусть дана система ур-ний с тремя неизвестными
Где коэффициенты
Для записи решения можно использовать формулу Крамера (если
№2.190. >> A=[7,2,3; 5,-3,2;10,-11,5] A = 7 2 3 5 -3 2 10 -11 5
>> B=[15;15;36] B =
>> d=A(1,1)*A(2,2)*A(3,3)+A(1,2)*A(2,3)*A(3,1)+A(2,1)*A(3,2)*A(1,3)-A(1,3)*A(2,2)*A(3,1)-A(2,3)*A(3,2)*A(1,1)-A(2,1)*A(1,2)*A(3,3) d = -36
>> d1=B(1)*A(2,2)*A(3,3)+A(1,2)*A(2,3)*B(3)+B(2)*A(3,2)*A(1,3)-A(1,3)*A(2,2)*B(3)-A(2,3)*A(3,2)*B(1)-B(2)*A(1,2)*A(3,3) d1 = -72 >> d2=A(1,1)*B(2)*A(3,3)+B(1)*A(2,3)*A(3,1)+A(2,1)*B(3)*A(1,3)-A(1,3)*B(2)*A(3,1)-B(3)*A(2,3)*A(1,1)-A(2,1)*B(1)*A(3,3) d2 = >> d3=A(1,1)*A(2,2)*B(3)+A(2,1)*A(3,2)*B(1)+A(1,2)*B(2)*A(3,1)-B(1)*A(2,2)*A(3,1)-B(2)*A(3,2)*A(1,1)-A(2,1)*A(1,2)*B(3) d3 = -36 >> x1=d1/d x1 = >> x2=d2/d x2 = -1 >> x3=d3/d x3 = Проверка: >> 7*x1+2*x2+3*x3 ans = 15 верно >> 5*x1-3*x2+2*x3 ans = 15 верно >> 10*x1-11*x2+5*x3 ans = 36 верно
№ 2.187 >> C=[3 -5; 2 7] C = 3 -5 2 7 >> B=[13;81] B = >> d=C(1,1)*C(2,2)-C(1,2)*C(2,1) d = >> d1=B(1)*C(2,2)-C(1,2)*B(2) d1 = >> d2=C(1,1)*B(2)-B(1)*C(2,1) d2 = >> x1=d1/d x1 = >> x2=d2/d x2 = Проверка: >> 3*x1-5*x2 ans = 13 верно
>> 2*x1+7*x2 ans = 81 верно
№2.188 >> C=[3 -4; 3 4]; >> B=[-6;18]; >> d=C(1,1)*C(2,2)-C(1,2)*C(2,1) d = >> d1=B(1)*C(2,2)-C(1,2)*B(2) d1 = >> d2=C(1,1)*B(2)-B(1)*C(2,1) d2 = >> x1=d1/d x1 = >> x2=d2/d x2 = >> 3*x1-4*x2 ans = -6 верно >> 3*x1+4*x2 ans = 18 верно >> A=[2,1,0; 1,0,3; 0,5,-1] A = 2 1 0 1 0 3 0 5 -1
>> B=[5;16;10] B = >> d=A(1,1)*A(2,2)*A(3,3)+A(1,2)*A(2,3)*A(3,1)+A(2,1)*A(3,2)*A(1,3)-A(1,3)*A(2,2)*A(3,1)-A(2,3)*A(3,2)*A(1,1)-A(2,1)*A(1,2)*A(3,3) d = -29 >> d1=B(1)*A(2,2)*A(3,3)+A(1,2)*A(2,3)*B(3)+B(2)*A(3,2)*A(1,3)-A(1,3)*A(2,2)*B(3)-A(2,3)*A(3,2)*B(1)-B(2)*A(1,2)*A(3,3) d1 = -29
>> d2=A(1,1)*B(2)*A(3,3)+B(1)*A(2,3)*A(3,1)+A(2,1)*B(3)*A(1,3)-A(1,3)*B(2)*A(3,1)-B(3)*A(2,3)*A(1,1)-A(2,1)*B(1)*A(3,3) d2= -87 >> d3=A(1,1)*A(2,2)*B(3)+A(2,1)*A(3,2)*B(1)+A(1,2)*B(2)*A(3,1)-B(1)*A(2,2)*A(3,1)-B(2)*A(3,2)*A(1,1)-A(2,1)*A(1,2)*B(3) d3 = -145 >> x1=d1/d x1 = >> x2=d2/d x2 = >> x3=d3/d x3 = Проверка: >> 2*x1+x2 ans = 5 верно >> x1+3*x3 ans = 16 верно >> 5*x2-x3 ans = 10 верно Данный номер я проделала сначала в тетради, затем в программе, я выявила, что вычислительных ошибок у меня нет
В лабораторной работе №2 по лин.алгебре я научилась пользоваться в программе MATLAB формулами для вычисления определителя 2 и 3 порядка. Занятие 3 Векторная алгебра Задание вектора и обращение к элементам вектора в системе MATLAB Упражнение 3.2 >> s1 = [3 4 9 2] s1 = 3 4 9 2 >> s2 = [5 3 3 2] s2 = 5 3 3 2 >> s3 = s1 + s2 s3 = 8 7 12 4 >> v1 = [2 -3 4 1]; >> v2 = [7 5 -6 9];
Упражнение 3.3 >> u=v1.*v2 u = 14 -15 -24 9 >> p = v1.^2 p = 4 9 16 1 >> v = [4 6 8 10]; >> p=v*2
p = 8 12 16 20 >> pi=2*v pi = 8 12 16 20 >> p=v/2 p = 2 3 4 5 >> length(s1) ans =
Упражнение 3.4 >> v1 = [1; 2] v1 = >> v2 = [3; 4; 5]; >> v = [v1; v2] v = >> v1 = [1 2]; v2 = [3 4 5]; v = [v1 v2] v = 1 2 3 4 5 Упражнение 3.6. В данном задании нужно с помощью спец.символов задать вектор-строку a и вектор-столбец b >> a=[2 4 6] a = 2 4 6 >> b=[1; 8; -2] b = -2 Изменим значение координаты ay на ‐5 >> a(2)=-5 a = 2 -5 6 Найдем значение координаты bz (сумма первой и второй координаты вектора b) >> b(3)=b(1)+b(2) b = Упражнение 3.9 правило параллелограмма. Дан параллелограмм ABCD, известны координаты трех его точек A(‐2 0), B(1 2), C(1 ‐1). Найти координаты четвертой вершины D параллелограмма. Показать на рисунке, что AB+ =AC, здесь AB, AD и AC – векторы. Изобразить векторы АВ и AD синим и АС красным, остальные стороны параллелограмма ВС и CD ‐черным. >> A=[-2 0]; B=[1 2]; C=[1 -1]; >> >> grid on, hold on >> xlabel('X'),ylabel('Y') >> line([-5 0;5 0],[0 -5;0 5],'color','black') >> line([A(1) B(1)],[A(2) B(2)],'LineWidth',4) >> text(-0.5,1.8,'{\bfAB}','Color','blue') >> text(-2,0.8,'A(-2;0)','Color','blue') >> text(1.2,1.5,'B(1;2)','Color','blue') >> line([A(1) C(1)],[A(2) C(2)],'LineWidth',4,'Color','red') >> text(1.2,-1,'C(1;-1)','Color','red') Найдем координаты точки D >> BA=A-B BA = -3 -2 >> BC=C-B BC = 0 -3 >> BD=BA+BC BD = -3 -5 >> D=BD+B D = -2 -3 >> line([A(1) D(1)],[A(2) D(2)],'LineWidth',4) >> text(-2.3,-3,'D(-2;-3)','Color','blue') >> text(-2.5,-2,'{\bfAB}','Color','blue') >> text(-1,-1,'{\bfAC}','Color','red') >> line([B(1) C(1)],[B(2) C(2)],'LineWidth',4, 'Color','black') >> line([C(1) D(1)],[C(2) D(2)],'LineWidth',4, 'Color','black') >> plot(B(1),B(2),'>b','LineWidth',4) >> plot(C(1),C(2),'>r','LineWidth',4) >> plot(D(1),D(2),'vb','LineWidth',4) Упражнение 3.10. grid on, xlabel('X'),ylabel('Y'),zlabel('Z') axis square box on line([0 1],[0 -2],[0 0]) line([0 0],[0 1],[0 1]) line([0 1],[0 2],[0 2]) line([0 1],[0 0],[0 0],'LineWidth',4,'color','black') >> line([0 0],[0 1],[0 0],'LineWidth',4,'color','black') line([0 0],[0 0],[0 1],'LineWidth',4,'color','black')
Упражнение 3.12 Вычислить скалярное произведение двух векторов a= {x1,y1,z1}, b= {x2,y2,z2} >> b = [x2,y2,z2]; >> a = [x1,y1,z1]; 1 способ >> axb = a(1)*b(1)+a(2)*b(2)+a(3)*b(3) axb = x1*x2 + y1*y2 + z1*z2
2 способ >> ab = a.*b ab = [ x1*x2, y1*y2, z1*z2]
>> ab = sum(ab) ab = x1*x2 + y1*y2 + z1*z2
3 способ >> axb = sum(a.*b) axb = x1*x2 + y1*y2 + z1*z2
Упражнение 3.13 Выразить скалярное произведение векторов A) в декартовом базисе >> p = [x1,y1,z1]; >> q = [x2,y2,z2]; >> a = [1,0,0]; >> b = [0,1,0]; >> c = [0,0,1]; >> p = x1*a + y1*b + z1*c; >> q = x2*a+y2*b+z2*c; >> pq = sum(p.*q) pq = x1*x2 + y1*y2 + z1*z2
B) косоугольном базисе >> a=[1,-2,0];b=[0,1,1];c=[1,2,2]; >> p=x1*a+y1*b+z1*c;q=x2*a+y2*b+z2*c; >> sum(p.*q) ans = (x1+z1)*(x2+z2)+(-2*x1+y1+2*z1)*(-2*x2+y2+2*z2)+(y1+2*z1)*(y2+2*z2) >>simplify(ans) ans = 5*x1*x2-3*x1*z2-2*x1*y2-3*z1*x2+9*z1*z2-2*y1*x2+2*y1*y2+4*y1*z2+4*z1*y2
C) в прямоугольном, но не в ортонормированном базисе >> a=[3,0,0];b=[0,4,0];c=[0,0,5]; >> p=x1*a+y1*b+z1*c;q=x2*a+y2*b+z2*c; >> pq=sum(p.*q) pq = 9*x1*x2+16*y1*y2+25*z1*z2
Вывод: выражение скалярного произведения в координатной форме существенно зависит от базиса, в котором заданы координаты векторов.
Векторное произведение Упражнение 3.14 Найти векторное произведение векторов >> a=[1,2,0];b=[2,1,0]; syms i j k [i,j,k;a;b] ans = [ i, j, k] [ 1, 2, 0] [ 2, 1, 0]
>> axb = det([i,j,k;a;b]) axb = (-3)*k >> A=[i,j,k;a;b] A = [ i, j, k] [ 1, 2, 0] [ 2, 1, 0] >> detA=A(1,1)*A(2,2)*A(3,3)+A(1,2)*A(2,3)*A(3,1)+A(2,1)*A(3,2)*A(1,3)-A(1,3)*A(2,2)*A(3,1)-A(2,3)*A(3,2)*A(1,1)-A(2,1)*A(1,2)*A(3,3)
detA = (-3)*k >> detA=A(1,1)*(A(2,2)*A(3,3)-A(2,3)*A(3,2))-A(1,2)*(A(2,1)*A(3,3)-A(2,3)*A(3,1))+A(1,3)*(A(2,1)*A(3,2)-A(2,2)*A(3,1)) detA = (-3)*k >> detA=det(a) ??? Error using ==> det Matrix must be square. >> detA=det(A) detA = (-3)*k >> cross(a,b) ans 0 0 -3 >> VECTab=det([i,j,k;a;b]) VECTab = (-3)*k Упражнение 3.15. Найти все векторы, перпендикулярные векторам >> a=[-1,3,2]; >>b=[3,-2,2]; >>det([i,j,k;a;b]) ans = 10*i + 8*j - 7*k >> ans*(-1) ans = 7*k - 8*j - 10*i >> cross(a,b) ans = 10 8 -7
Упражнение 3.16.Упростить выражение >> syms a1 a2 a3 b1 b2 b3 >> a=[a1 a2 a3];b=[b1 b2 b3]; >> ans1= cross(a,b) ans1 = [ a2*b3 - a3*b2, a3*b1 - a1*b3, a1*b2 - a2*b1] >> ans2=cross(a+2*b,a-2*b) ans2 =
[ (a2 + 2*b2)*(a3 - 2*b3) - (a2 - 2*b2)*(a3 + 2*b3), (a1 - 2*b1)*(a3 + 2*b3) - (a1 + 2*b1)*(a3 - 2*b3), (a1 + 2*b1)*(a2 - 2*b2) - (a1 - 2*b1)*(a2 + 2*b2)] >> simplify(ans2) ans = [ 4*a3*b2 - 4*a2*b3, 4*a1*b3 - 4*a3*b1, 4*a2*b1 - 4*a1*b2] >> ans2./ans1 ans = [ -((a2 - 2*b2)*(a3 + 2*b3) - (a2 + 2*b2)*(a3 - 2*b3))/(a2*b3 - a3*b2), -((a1 - 2*b1)*(a3 + 2*b3) - (a1 + 2*b1)*(a3 - 2*b3))/(a1*b3 - a3*b1), -((a1 - 2*b1)*(a2 + 2*b2) - (a1 + 2*b1)*(a2 - 2*b2))/(a1*b2 - a2*b1)] >> simplify(ans) ans = [ -4, -4, -4]
Вывод Вывод. Скалярное произведение тех же векторов преобразуется к совершенно иному виду, а именно,
Упражнение 3.17. Найти векторное произведение векторов >> a=[1,2,0];b=[2,1,0]; >> c=cross(a,b)
c =
0 0 -3
>> grid on, hold on >> xlabel('X'),ylabel('Y'),zlabel('Z') >> axis square >> line([-5 0 0;5 0 0], [0 -5 0;0 5 0],[0 0 -5;0 0 5],'Color','black') >> line([0 1],[0,2],'LineWidth',2) >> plot3(1,2,0,'>','LineWidth',2) >> line([0 2],[0,1],'Color','green','LineWidth',2) >> plot3(2,1,0,'>g','LineWidth',2) >> line([0 0],[0,0],[0 -3],'Color','red','LineWidth',2) >> plot3(0,0,-3,'>r','LineWidth',2) >> plot3(5,0,0,'<k','LineWidth',2) >> plot3(0,5,0,'<k','LineWidth',2) >> plot3(0,0,5,'<k','LineWidth',2) >> text(4.5,-0.5,0.8,'X') >> text(-0.5,4.5,0.8,'Y') >> text(-0.5,-1,4.5,'Z') Выводы: Синий вектор Изобразим плоскость желтого параллелограмма: >> x1=0:0.1:1.9;y1=0:0.05:0.95;x2=1:0.1:2.9;y2=2:0.05:2.95; >> line([x1; x2],[y1; y2],'Color','yellow','LineWit') Упражнение 3.18 Вычислить площадь треугольника с вершинами >> A=[1,3,-1] A = 1 3 -1 >> B=[2,-1,4] B = 2 -1 4 >> C=[5,0,3] C = 5 0 3 >> AB = B-A AB = 1 -4 5 >> AC = C-A AC = 4 -3 4 >> modAB = sqrt(1+4^2+5^2) modAB = 6.4807 >> modAC = sqrt(4^2+3^2+4^2) modAC = 6.4031 >> cosA = sum(AB.*AC)/(modAC*modAB) cosA =
0.8675 >> sinA = sqrt(1 - cosA^2) sinA = 0.4974 >> axb = cross(AB,AC) axb = -1 16 13 >> modaxb = sqrt(1^2+16^2+13^2) modaxb = 20.6398 >> S = modAB*modAC*sinA/2 S = 10.3199 >> modaxb/S ans = Значит, модуль векторного произведения в 2 раза больше площади треугольника, построенного на этих векторах. >> hold on >> grid on >> box on >> axis square >> plot3(5,0,3,'.') >> plot3(2,-1,4,'.') >> plot3(1,3,-1,'.') >> xlabel('X'),ylabel('Y'),zlabel('Z') >> line([-5 0 0;5 0 0],[0 -5 0;0 5 0],[0 0 -5;0 0 5],'Color','k') >> line([1:0.04:5;2:0.00002:2.002],[3:-0.03:0;-1:-0.00002:-1.002],[-1:0.04:3;4:0.00002:4.002],'Color','b','LineWidth',2) Упражнение 3.19 Найти смешанное произведение векторов >> a = [a1,a2,a3]; >> c = [c1,c2,c3]; >> b = [b1,b2,b3]; >> abc = sum(cross(a,b).*c)
abc =
a1*b2*c3 - a1*b3*c2 - a2*b1*c3 + a2*b3*c1 + a3*b1*c2 - a3*b2*c1
>> abc1 = det([a;b;c])
abc1 =
a1*b2*c3 - a1*b3*c2 - a2*b1*c3 + a2*b3*c1 + a3*b1*c2 - a3*b2*c1
>> bac = sum(cross(b,a).*c)
bac =
a1*b3*c2 - a1*b2*c3 + a2*b1*c3 - a2*b3*c1 - a3*b1*c2 + a3*b2*c1
>> bac/abc
ans =
-1 Упражнение 3.20 >> a = [1,-2,0]; >> b = [0,1,1]; >> c = [1,2,2]; >> det([a;b;c])
ans =
-2 Смешанное произведение <0, значит a,b,c – левая тройка, И векторы a,b,c – некомпланарные. Компланарные векторы не могут линейно независимы и не могут образовать базис. >> box on >> grid on >> hold on >> line([0;a(1)],[0;a(2)],[0;a(3)]) >> line([0;b(1)],[0;b(2)],[0;b(3)],'Color','g') >> line([0;c(1)],[0;c(2)],[0;c(3)],'Color','r') >> line([-5 0 0;5 0 0],[0 -5 0;0 5 0],[0 0 -5;0 0 5],'Color','k')
Упражнение 3.21 Исследовать с помощью смешанного произведения векторы >> syms a b c p q r >> p = [a -b c]
p =
[ a, -b, c]
>> q = [-a b -c]
q =
[ -a, b, -c]
>> r = [0 b -c]
r =
[ 0, b, -c]
>> sum(cross(p,q).*r)
ans =
Векторы p,q,r – компланарные. >> p = [2*a b c]
p =
[ 2*a, b, c]
>> q = [ a b 0]
q =
[ a, b, 0]
>> r = [0 b -c]
r =
[ 0, b, -c]
>> sum(cross(p,q).*r)
ans =
Векторы компланарные.
>> p = [a -b c]
p =
[ a, -b, c]
>> q = [a b 0]
q =
[ a, b, 0]
>> r = [0 b -c]
r =
[ 0, b, -c]
>> sum(cross(p,q).*r)
ans =
-a*b*c Векторы некомпланарные.
Упражнение 3.22 Вычислить >> syms a1 a2 a3 b1 b2 b3 c1 c2 c3 >> a = [a1,a2,a3]; >> b = [b1,b2,b3]; >> c = [c1,c2,c3]; >> sum(cross(a+2*b-c,3*a-b).*(2*a+2*b+c))
ans =
15*a1*b3*c2 - 15*a1*b2*c3 + 15*a2*b1*c3 - 15*a2*b3*c1 - 15*a3*b1*c2 + 15*a3*b2*c1 >> A = det([a;b;c])
A =
a1*b2*c3 - a1*b3*c2 - a2*b1*c3 + a2*b3*c1 + a3*b1*c2 - a3*b2*c1
>> res = sum(cross(a+2*b-c,3*a-b).*(2*a+2*b+c))
res =
15*a1*b3*c2 - 15*a1*b2*c3 + 15*a2*b1*c3 - 15*a2*b3*c1 - 15*a3*b1*c2 + 15*a3*b2*c1
>> res/A
ans =
-(15*a1*b2*c3 - 15*a1*b3*c2 - 15*a2*b1*c3 + 15*a2*b3*c1 + 15*a3*b1*c2 - 15*a3*b2*c1)/(a1*b2*c3 - a1*b3*c2 - a2*b1*c3 + a2*b3*c1 + a3*b1*c2 - a3*b2*c1)
>> simplify(ans)
ans =
-15 Значит [a+2b-c,3a-b],(2a+2b+c) = -15A.
Упражнение 3.23 Пусть >> syms a b c p q r l >> q = [3*a b -c]
q =
[ 3*a, b, -c]
>> p = [a -2*b l*c]
p =
[ a, -2*b, c*l]
>> r = [a 0 -1*l*c]
r =
[ a, 0, -c*l]
>> det([p;q;r])
ans =
2*a*b*c - 8*a*b*c*l
>> simplify(ans)
ans =
(-2)*a*b*c*(4*l - 1) Значит, при l = ¼, векторное произведение будет равно нулю, и векторы p,q,r будут компланарны
Модуль 1 Векторная алгебра Арифметические вычисления. Упражение 1 Постановка задачи Знакомство с MATLAB. Изучение команд Упражнение 1.1 >> 1+2 ans = >> ans/4.5 ans = 0.6667 Упражнение 1.2 >> 1/2+2/3 ans = 1.1667
>> format rat 1/2+2/3 ans = 7/6 Упражнение 1.3 >> syms x >> f=(x+1)*(x-1) f = (x - 1)*(x + 1)
>> collect(f) ans = x^2 - 1 >> f=collect(f) f = x^2 – 1
Переменные рабочего пространства. >> x=1, y=2, z=3, t=4 x =
y =
z =
t =
>> whos x y z t Name Size Bytes Class Attributes
t 1x1 8 double x 1x1 8 double y 1x1 8 double z 1x1 8 double >> clear x >> whos y z t Name Size Bytes Class Attributes t 1x1 8 double y 1x1 8 double z 1x1 8 double
>> clear y z >> whos Name Size Bytes Class Attributes t 1x1 8 double
|
||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 164; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |


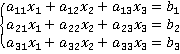
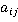 , i= 1,2,3; j =1,2,3 пр неизвестных
, i= 1,2,3; j =1,2,3 пр неизвестных 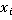 , i=1,2,3 и свободные члены
, i=1,2,3 и свободные члены  , i=1,2,3
, i=1,2,3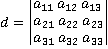 ,
,  ,
,  ,
, 
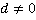 ).
).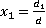
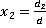

 ,
, 
 ,
,  и
и 
 ,
, 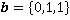 и
и  . Пользуясь геометрическим свойством скалярного произведения, убедиться, что векторы a,b,c образуют косоугольный базис.
. Пользуясь геометрическим свойством скалярного произведения, убедиться, что векторы a,b,c образуют косоугольный базис. ,
, 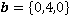 и
и 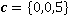
 и
и  с помощью определителя третьего порядка см формулу (8) и проверить решение стандартной функцией cross(a,b)
с помощью определителя третьего порядка см формулу (8) и проверить решение стандартной функцией cross(a,b) и
и 
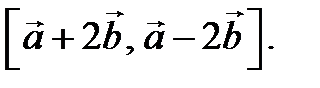 Затем найти скалярное произведение тех же векторов.
Затем найти скалярное произведение тех же векторов.
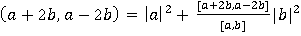
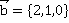 . Изобразить все данные и результат. Первый вектор изобразить синим, второй зеленым, результат красным. Сделать выводы: как связаны определение векторного произведения и то, что мы получили на рисунке.
. Изобразить все данные и результат. Первый вектор изобразить синим, второй зеленым, результат красным. Сделать выводы: как связаны определение векторного произведения и то, что мы получили на рисунке. , зеленый вектор
, зеленый вектор  и красный вектор
и красный вектор  образуют правую тройку. Вектор
образуют правую тройку. Вектор  перпендикулярен плоскости векторов
перпендикулярен плоскости векторов  и
и  .
.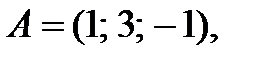
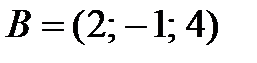 и
и 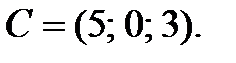 Изобразить плоскость треугольника. Как соотносятся площадь треугольника и векторное произведение. Изобразить это соответствие по аналогии с предыдущим упражнением.
Изобразить плоскость треугольника. Как соотносятся площадь треугольника и векторное произведение. Изобразить это соответствие по аналогии с предыдущим упражнением. , где векторы
, где векторы  и
и  перемножаются векторно, а их результат на вектор
перемножаются векторно, а их результат на вектор  скалярно.
скалярно. на компланарность, векторы
на компланарность, векторы 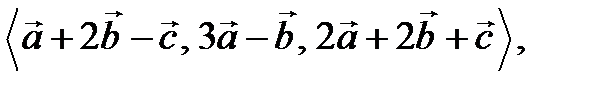 если
если  = А.
= А. – некомпланарные векторы. Найти значение
– некомпланарные векторы. Найти значение 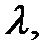 при котором следующие векторы компланарны:
при котором следующие векторы компланарны: