Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Упражнение 3.1. Ввод сложение и вычитание векторов
>> a = [1.3; 5.4; 6.9] a = 1.3000 5.4000 6.9000 >> b = [7.1; 3.5; 8.2]; >> c = a + b c = 8.4000 8.9000 15.1000
>> ndims(a) ans = >> size(a) ans = 3 1 >> ndims(b) ans = >> size(b) ans = 3 1 >> ndims(c) ans = >> size(c) ans = 3 1
Упражнение 3.2 >> s1 = [3 4 9 2] s1 = 3 4 9 2 >> s2 = [5 3 3 2] s2 = 5 3 3 2 >> s3 = s1 + s2 s3 = 8 7 12 4 >> v1 = [2 -3 4 1]; >> v2 = [7 5 -6 9];
Упражнение 3.3 >> u=v1.*v2 u = 14 -15 -24 9 >> p = v1.^2 p = 4 9 16 1 >> v = [4 6 8 10]; >> p=v*2
p = 8 12 16 20 >> pi=2*v pi = 8 12 16 20 >> p=v/2 p = 2 3 4 5 >> length(s1) ans =
Упражнение 3.4 >> v1 = [1; 2] v1 = >> v2 = [3; 4; 5]; >> v = [v1; v2] v = >> v1 = [1 2]; v2 = [3 4 5]; v = [v1 v2] v = 1 2 3 4 5 Упражнение. 3.5. Работа с элементами векторов. >> v = [1.3 3.6 7.4 8.2 0.9]; >> v(4) ans = 8.2000 >> v(2) = 555 v = 1.3000 555.0000 7.4000 8.2000 0.9000 >> u = [v(3); v(2); v(1)] u = 7.4000 555.0000 1.3000
>> ind = [4 2 5] ind = 4 2 5 >> w = v(ind) w = 8.2000 555.0000 0.9000 >> w = [0.1 2.9 3.3 5.1 2.6 7.1 9.8] w = 0.1000 2.9000 3.3000 5.1000 2.6000 7.1000 9.8000 >> w(2:6) = 0 w = 0.1000 0 0 0 0 0 9.8000 >> w = [0.1 2.9 3.3 5.1 2.6 7.1 9.8] w = 0.1000 2.9000 3.3000 5.1000 2.6000 7.1000 9.8000
>> wl = w(3:5) wl = 3.3000 5.1000 2.6000 >> w2 = [w(1:3) w(5:7)] w2 = 0.1000 2.9000 3.3000 2.6000 7.1000 9.8000 >> gm = (u(1)*u(2)*u(3))^(1/3) gm = 17.4779
Упражнение 3.6. В данном задании нужно с помощью спец.символов задать вектор-строку a и вектор-столбец b >> a=[2 4 6] a = 2 4 6 >> b=[1; 8; -2] b = -2 Изменим значение координаты ay на ‐5 >> a(2)=-5 a = 2 -5 6 Найдем значение координаты bz (сумма первой и второй координаты вектора b) >> b(3)=b(1)+b(2) b = Линейные операции над векторами и их свойства. сумма двух векторов может быть найдена: а) по правилу треугольника; б) по правилу параллелограмм
Упражнение 3.7. Правило треугольника. >> A=[-2 0]; B=[1 2]; C=[1 -1]; >> line([A(1),B(1)],[A(2),B(2)]) >>grid on, hold on >>xlabel('X'),ylabel('Y') >>line([-5 0;5 0],[0 -5;0 5],'color','black') >>line([A(1) B(1)],[A(2) B(2)],'LineWidth',4) >>line([B(1) C(1)],[B(2) C(2)],'LineWidth',4) >>line([C(1) A(1)],[C(2) A(2)],'LineWidth',4,'Color','red') >>text(-2,0.8,'A(-2;0)','Color','blue') >>text(1.2,1.5,'B(1;2)','Color','blue') >>text(-0.5,1.8,'{\bfAB}','Color','blue') >>text(1.2,-1,'C(1;-1)','Color','blue') >>text(-2,-0.5,'A(-2;0)','Color','red') >> text(1.5,0.5,'{\bfBC}','Color','blue') >>text(-1,-1,'{\bfAC}','Color','red') >>title('Правило треугольника {\bfAB+BC=AC}') >> plot(C(1),C(2),'>r','LineWidth',4) >> plot(B(1),B(2),'>r','LineWidth',4) >> plot(B(1),B(2),'>b','LineWidth',4) >> plot(1,-0.8,'vb','LineWidth',4)
Упражнение 3.9 правило параллелограмма. Дан параллелограмм ABCD, известны координаты трех его точек
A(‐2 0), B(1 2), C(1 ‐1). Найти координаты четвертой вершины D параллелограмма. Показать на рисунке, что AB+ =AC, здесь AB, AD и AC – векторы. Изобразить векторы АВ и AD синим и АС красным, остальные стороны параллелограмма ВС и CD ‐черным. >> A=[-2 0]; B=[1 2]; C=[1 -1]; >> >> grid on, hold on >> xlabel('X'),ylabel('Y') >> line([-5 0;5 0],[0 -5;0 5],'color','black') >> line([A(1) B(1)],[A(2) B(2)],'LineWidth',4) >> text(-0.5,1.8,'{\bfAB}','Color','blue') >> text(-2,0.8,'A(-2;0)','Color','blue') >> text(1.2,1.5,'B(1;2)','Color','blue') >> line([A(1) C(1)],[A(2) C(2)],'LineWidth',4,'Color','red') >> text(1.2,-1,'C(1;-1)','Color','red') Найдем координаты точки D >> BA=A-B BA = -3 -2 >> BC=C-B BC = 0 -3 >> BD=BA+BC BD = -3 -5 >> D=BD+B D = -2 -3 >> line([A(1) D(1)],[A(2) D(2)],'LineWidth',4) >> text(-2.3,-3,'D(-2;-3)','Color','blue') >> text(-2.5,-2,'{\bfAB}','Color','blue') >> text(-1,-1,'{\bfAC}','Color','red') >> line([B(1) C(1)],[B(2) C(2)],'LineWidth',4, 'Color','black') >> line([C(1) D(1)],[C(2) D(2)],'LineWidth',4, 'Color','black') >> plot(B(1),B(2),'>b','LineWidth',4) >> plot(C(1),C(2),'>r','LineWidth',4) >> plot(D(1),D(2),'vb','LineWidth',4) Линейная зависимость векторов Линейной комбинацией векторов Линейная комбинация называется нетривиальной, если хотя бы один из ее коэффициентов отличен от нуля. Упражнение 3.10. grid on, xlabel('X'),ylabel('Y'),zlabel('Z') axis square box on line([0 1],[0 -2],[0 0]) line([0 0],[0 1],[0 1]) line([0 1],[0 2],[0 2]) line([0 1],[0 0],[0 0],'LineWidth',4,'color','black') >> line([0 0],[0 1],[0 0],'LineWidth',4,'color','black') line([0 0],[0 0],[0 1],'LineWidth',4,'color','black')
Упражнение 3.12 Вычислить скалярное произведение двух векторов a= {x1,y1,z1}, b= {x2,y2,z2} >> b = [x2,y2,z2]; >> a = [x1,y1,z1]; 1 способ >> axb = a(1)*b(1)+a(2)*b(2)+a(3)*b(3) axb = x1*x2 + y1*y2 + z1*z2
2 способ >> ab = a.*b ab = [ x1*x2, y1*y2, z1*z2]
>> ab = sum(ab) ab = x1*x2 + y1*y2 + z1*z2
3 способ >> axb = sum(a.*b) axb = x1*x2 + y1*y2 + z1*z2
Упражнение 3.13 Выразить скалярное произведение векторов A) в декартовом базисе >> p = [x1,y1,z1]; >> q = [x2,y2,z2]; >> a = [1,0,0]; >> b = [0,1,0]; >> c = [0,0,1]; >> p = x1*a + y1*b + z1*c; >> q = x2*a+y2*b+z2*c; >> pq = sum(p.*q) pq = x1*x2 + y1*y2 + z1*z2
B) косоугольном базисе >> a=[1,-2,0];b=[0,1,1];c=[1,2,2]; >> p=x1*a+y1*b+z1*c;q=x2*a+y2*b+z2*c; >> sum(p.*q) ans = (x1+z1)*(x2+z2)+(-2*x1+y1+2*z1)*(-2*x2+y2+2*z2)+(y1+2*z1)*(y2+2*z2)
>>simplify(ans) ans = 5*x1*x2-3*x1*z2-2*x1*y2-3*z1*x2+9*z1*z2-2*y1*x2+2*y1*y2+4*y1*z2+4*z1*y2
C) в прямоугольном, но не в ортонормированном базисе >> a=[3,0,0];b=[0,4,0];c=[0,0,5]; >> p=x1*a+y1*b+z1*c;q=x2*a+y2*b+z2*c; >> pq=sum(p.*q) pq = 9*x1*x2+16*y1*y2+25*z1*z2
Вывод: выражение скалярного произведения в координатной форме существенно зависит от базиса, в котором заданы координаты векторов.
Векторное произведение
|
||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 115; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.146.105.194 (0.083 с.) |

 с коэффициентами
с коэффициентами  будем называть конечную сумму вида
будем называть конечную сумму вида 
 ,
, 
 ,
,  и
и 
 ,
, 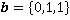 и
и  . Пользуясь геометрическим свойством скалярного произведения, убедиться, что векторы a,b,c образуют косоугольный базис.
. Пользуясь геометрическим свойством скалярного произведения, убедиться, что векторы a,b,c образуют косоугольный базис. ,
, 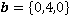 и
и