
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Построение структурных схем по дифференциальным уравнениям.
Способ составления структурной схемы, основанный на использовании дифференциальных уравнений. Рассмотрим его сначала для объекта, поведение которого описывают векторно-матричные уравнения
Проинтегрируем уравнение состояния в по времени и определим переменные состояния и выхода:
Структурную схему, соответствующую данным уравнениям, удобнее изображать, начиная с выходных переменных y, причем входные и выходные переменные объекта желательно располагать на одной горизонтальной прямой. Для одноканального объекта структурную схему можно составить по уравнению
разрешив его относительно старшей производной Проинтегрировав n раз, получим
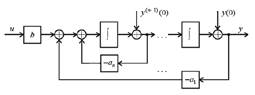
Этой системе уравнений соответствует структурная схема, приведенная на рисунке
Как видим, одноканальный объект управления, поведение которого описывает уравнение, структурно всегда можно представить в виде цепочки из n последовательно соединенных интеграторов с обратными связями.
Первая каноническая Рассмотрим преобразование математической модели системы с передаточной функцией (3.64). Ее структурную схему можно представить в виде двух последовательно соединенных звеньев (рис. 3.39).
Для каждого звена системы запишем соответствующее операторное уравнение:
Определим из первого уравнения (3.66) старшую производную переменной z, что соответствует значению pnz в операторной форме
Переменные состояния введем
Вторая каноническая Рассмотрим второй способ перехода от передаточной функции (3.63) к описанию в переменных состояния, для чего структуру системы (3.65) схематично представим на рис. 3.42. Ее операторные уравнения имеют вид
Представим первое уравнение (3.68) в виде цепочки из n интеграторов с обратными связями, а входное воздействие z1 сформируем в соответствии со вторым уравнением (3.68) в виде суммы управления u и m его производных (рис. 3.43).
В результате структурных преобразований получим структурную схему системы, приведенную на рис. 3.44. Как видим, и в этом случае структурная схема, соответствующая передаточной функции (3.65), состоит из цепочки n интеграторов. В обратной связи также располагаются коэффициенты характеристического полинома, а в прямой связи – коэффициенты полинома ее числителя.
Снова в качестве переменных состояния используем выходные величины интеграторов и запишем относительно их дифференциальные уравнения состояния и уравнение выхода
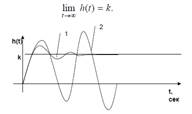
Устойчивость динамических систем. Методы анализа устойчивости линейных систем. Основные понятия и определения. Общее условие устойчивости линейных систем. Алгебраические и частотные критерии устойчивости: Гурвица, Михайлова, Найквиста. Области и запасы устойчивости. Основные понятия и определения. Физически устойчивость означает, что при ограниченном входном сигнале выходной сигнал также является ограниченным и процессы в системе стремятся к определенному значению при любых начальных условиях. Для переходной характеристики устойчивой системы справедливо условие
1 – сходящийся процесс, система устойчива; 2 – расходящийся процесс, система неустойчива Об устойчивости можно судить также по импульсным переходным функциям, которые в случае устойчивой системы удовлетворяют условию
Рассмотрим, как можно оценить это свойство для систем, поведение которых описывают уравнения
Определим зависимость переменных состояния от времени как решение векторно-матричного уравнения состояния в виде
Первое слагаемое соответствует свободной составляющей движения (из произвольных начальных условий), второе – вынужденной (движение под действием управления). Запишем уравнение статики, полагая в (4.1)
откуда при det A≠0 определим равновесное значение переменных состояния
Введем новые координаты, равные отклонениям от точки равновесия,
После подстановки в (4.6) вместо его Учитывая (4.4), уравнение в отклонениях принимает вид
Как видим, уравнение (4.7) не содержит u, и поэтому переходный процесс по Δ порождается только ненулевыми начальными условиями согласно уравнению
Линейная система (4.1) называется устойчивой, если для ее процессов выполняется условие
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-06; просмотров: 2207; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.17.46 (0.009 с.) |









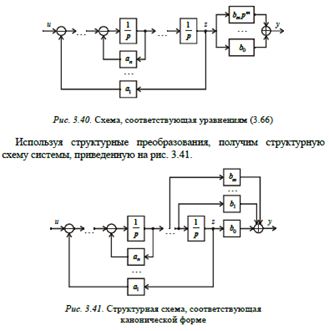 Полученное выражение позволяет представить первое уравнение (3.66) в виде цепочки из n интеграторов с обратными связями, а выходная переменная y формируется в соответствии со вторым уравнением (3.66) как сумма переменной z и ее m производных (рис. 3.40).
Полученное выражение позволяет представить первое уравнение (3.66) в виде цепочки из n интеграторов с обратными связями, а выходная переменная y формируется в соответствии со вторым уравнением (3.66) как сумма переменной z и ее m производных (рис. 3.40).










 и запишем для них ДУ
и запишем для них ДУ  так как x0=0.
так как x0=0. значения из (4.1) с учетом (4.5) получим
значения из (4.1) с учетом (4.5) получим 






