
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгебраические и частотные критерии устойчивости.
Критерий Гурвица Он является алгебраическим и связывает расположение корней характеристического уравнения с определенными условиями, которые накладываются на его коэффициенты.
по следующему правилу составляется матрица Гурвица: на главной диагонали сверху вниз выписываются по порядку коэффициенты характеристического уравнения от до включительно. В каждом столбце вниз от диагонали записывают коэффициенты при возрастающих степенях оператора p, вверх – при убывающих степенях p. Недостающие элементы в столбце дополняются нулями.
Формулировка. Для устойчивости линейной системы необходимо и достаточно, чтобы все n диагональных миноров, полученных из матрицы Гурвица H, были положительны:
Здесь Δi– определители Гурвица, которые составляются следующим образом:
Поскольку определитель n-1 –го порядка должен быть положительным, последнее условие соответствует требованию a1>0. Следствием критерия является условие границы устойчивости, когда последний определитель Гурвица обращается в нуль:
Критерий Найквиста Позволяет определить устойчивость системы с отрицательной обратной связью (так называемой замкнутой системы) по экспериментально снятой или полученной на основе передаточной функции амплитудно-фазовой частотной характеристики разомкнутой системы.
Рассмотрим этот критерий для системы с единичной обратной связью Здесь W0(p)– передаточная функция устойчивой разомкнутой системы, которая в общем случае имеет вид:
Определим передаточную функцию системы, изображенной на рис.
Формулировка: для устойчивости замкнутой системы необходимо и достаточно, чтобы амплитудно-фазовая характеристика устойчивой разомкнутой системы при изменении ω от 0 до ∞ не охватывала точку с координатами -1; j0.
Разомкнутая система может быть неустойчива, однако это не означает, что неустойчивой будет и замкнутая система. В этой ситуации следует использовать видоизмененную формулировку критерия Найквиста: замкнутая система будет устойчива тогда и только тогда, когда амплитудно-фазовая характеристика неустойчивой разомкнутой системы при изменении ω от 0 до ∞ охватывает точку с координатами -1; j0 в положительном направлении r/2 раз, где r– число корней характеристического уравнения разомкнутой системы с положительной вещественной частью.
Сформулируем теперь условие границы устойчивости. Замкнутая система будет находиться на границе устойчивости, если при некоторой частоте ω = ω0 АФХ разомкнутой системы проходит через точку с координатами -1; j0. Аналитически это условие можно записать в виде:
Предварительно необходимо получить передаточную функцию разомкнутой системы, для чего можно размыкать связь произвольным образом, а вход и выход системы следует рассматривать в месте разрыва. В результате искомая передаточная функция будет иметь вид:
Критерий Михайлова Он базируется на принципе аргумента теории функций комплексной переменной. Для анализа устойчивости системы предлагается исследовать характеристический комплекс F(jω), который получается из характеристического полинома:
заменой p на jω
Выделим в (4.14) вещественную и мнимую части, а также модуль и фазу:
При конкретном численном значении частоты (ω=ω1) характеристический комплекс (4.19) представляет собой комплексное числоF(j При изменении ω от 0 до ∞ конец вектора F(jω)выписывает на комплексной плоскости некоторую кривую, которую называют годографом Михайлова (см. рис.). Причем начинается годограф, как следует из соотношения (4.18), в точке с координатами a1, j0.
Формулировка. Для устойчивости линейной системы необходимо и достаточно, чтобы годограф Михайлова при изменении от ω от 0 до ∞ начинался на вещественной оси в точке и проходил последовательно против часовой стрелки n квадрантов комплексной плоскости, не обращаясь в нуль и стремясь к в n-м квадранте в ∞.
Условием границы устойчивости является обращение в нуль годографа Михайлова при некотором значении частоты ω = ω0. Аналитически это условие можно записать в виде:
Здесь ω0 – частота незатухающих колебаний, возникающих в системе, которая находится на границе устойчивости.
|
||||||
|
Последнее изменение этой страницы: 2017-02-06; просмотров: 383; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.42.168 (0.008 с.) |






 где ее характеристический полином
где ее характеристический полином 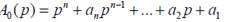 .
. где
где  характеристический полином замкнутой системы.
характеристический полином замкнутой системы.







 ) которое можно изобразить на плоскости в виде вектора, соединяющего начало координат с точкой RF(
) которое можно изобразить на плоскости в виде вектора, соединяющего начало координат с точкой RF(





