Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Из стереометрии известно: если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны.Содержание книги
Поиск на нашем сайте
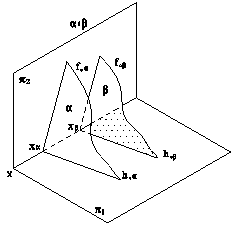
Пример 2 (рис.4.2). Через точку А провести плоскость b, параллельную плоскости a(аÇb).
Рис.4.2 Решение: Проведем через точку А прямые с и d, соответственно параллельные прямым а и b заданной плоскости a, получим плоскость b(сÇd), параллельную заданной плоскости. Две плоскости a(h0aÇf0a) и b(h0bÇf0b) будут параллельны между собой, если одноименные следы этих плоскостей будут попарно параллельны (рис.4.3).
Рис.4.3а Рис.4.3б
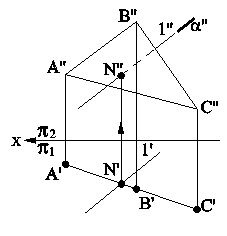
ВЗАИМНОЕ ПЕРЕСЕЧЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ. Задача на взаимное пересечение прямой и плоскости может быть сведена к одному из трех типов задач: 1. Обе геометрические фигуры проецирующего положения по отношению к плоскостям проекций (рис.4.4а и 4.4б).
Рис.4.4а Рис.4.4б
В этом случае искомый элемент - точка пересечения на чертеже уже есть, ее надо только выделить и обозначить. 2. Одна из заданных фигур проецирующего положения в пространстве, а другая - общего (рис.4.5а и 4.5б).
Рис.4.5а Рис.4.5б
В этом случае одна из проекций искомой точки пересечения на чертеже уже есть. Она принадлежит геометрической фигуре проецирующего положения, а другая ее проекция находится по принадлежности к фигуре непроецирующего положения. 3. Обе геометрические фигуры - линия и плоскость - общего положения в пространстве по отношению к плоскостям проекций. В этом случае задача решается с помощью вспомогательной секущей плоскости в качестве “посредника”, которую проводят через заданную прямую. На рис.4.6а и 4.6б приведены примеры пересечения прямой l с плоскостью треугольника АВС и прямой а с плоскостью b, заданной следами.
Рис.4.6а Рис.4.6б
ВЗАИМНОЕ ПЕРЕСЕЧЕНИЕ ДВУХ ПЛОСКОСТЕЙ Эта задача может быть сведена к одному из трех типов задач, рассмотренных выше (случаи пересечения прямой с плоскостью). 1. Обе плоскости проецирующего положения по отношению одной или разным плоскостям проекций (рис.4.7).
Рис.4.7 В этом случае искомая линия пересечения плоскостей на чертеже уже есть. Ее нужно только выделить и обозначить.
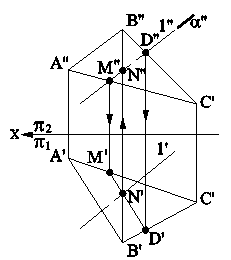
2. Одна из плоскостей проецирующего положения, а другая - общего положения (рис.4.8а и 4.8б).
Рис.4.8а Рис.4.8б
3. Обе плоскости общего положения в пространстве. В этом случае задача решается с помощью двух вспомогательных секущих плоскостей в качестве посредников. Такими посредниками будут проецирующие плоскости.
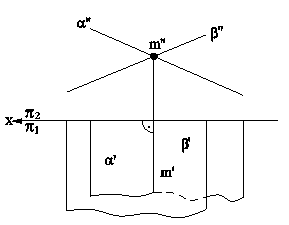
Пример 1 (рис.4.9). Найти линию пересечения двух плоскостей: a(а||b) и b(c ∩ d).
Рис.4.9
ВЗАИМНОЕ ПЕРЕСЕЧЕНИЕ ПЛОСКОСТЕЙ, ЗАДАННЫХ СЛЕДАМИ. Линия взаимного пересечения плоскостей, заданных следами, проходит через точки пересечения их одноименных следов. Решение задачи показано на рис.4.10а и 4.10б.
Рис.4.10а Рис.4.10б
Литература:
Фролов С.А. Начертательная геометрия. 2-е изд., изд.Машиностр. 1983., §§44;с.170. Гордон В.О. и др. Курс начерт. геом., Глава IV до перпендикулярности. Локтев В.О. Краткий курс начерт.геом. 1985. §§11, 12.
ИЗОБРАЖЕНИЕ МНОГОГРАННИКОВ Многогранником называют тело, ограниченное плоскими многоугольниками. Многогранник, расположенный по одну сторону от плоскости его грани, называют выпуклым. Грани, вершины и ребра многогранников связаны между собой соотношением, называемым теоремой Л.Эйлера: Г+В-Р=2, где: Г - число граней, В - число вершин и Р - число ребер. Число граней многогранника не может быть меньше четырех, а сумма углов многоугольников, сходящихся в одной вершине, многогранных углов, не должно быть больше 2p. Основные виды многогранников: пирамида, призма, правильные многогранники и многогранники, имеющие соответствующие одинаковые двугранные углы. Многогранник представляет собой частный случай замкнутой многогранной поверхности.
ВИДЫ МНОГОГРАННИКОВ Призмой называют многогранник, у которого две одинаковые взаимно параллельные грани - основания, а остальные грани - параллелограммы. Пирамида представляет собой многогранник, у которого одна грань (произвольный многоугольник) принимается за основание, а остальные (боковые) грани - треугольники с общей вершиной. Правильными называются такие многогранники, у которых все грани - правильные равные многоугольники. Так как в каждой вершине многогранника должны сходиться не меньше трех многоугольников, а у правильного многоугольника все углы равны, то величина угла многоугольника (грани) должна быть меньше 2p/3. В правильном шестиугольнике углы равны 2p/3, поэтому в правильном многограннике грань не может быть шестиугольником. Из сказанного можно сделать вывод, что правильных многогранников может быт только пять. В качестве граней правильных многогранников могут быть только правильный треугольник, четырехугольник и пятиугольник.
Правильными многогранниками являются: 1. правильный четырехгранник или тетраэдр (грань - правильный треугольник), 2. правильный шестигранник (куб) или гексаэдр (грань квадрат), 3. правильный восьмигранник или октаэдр (грань правильный треугольник), 4. правильный двенадцатигранник или додекаэдр (грань - правильный пятиугольник), 5. правильный двенадцатигранник или икосаэдр (грань - правильный треугольник). Правильные многогранники называют Платоновыми телами. При изображении многогранника видимость его ребер и граней определяется с помощью конкурирующих точек. ПЕРЕСЕЧЕНИЕ ПРЯМОЙ ЛИНИИ С ПОВЕРХНОСТЬЮ МНОГОГРАННИКА Задача на пересечение прямой с поверхностью многогранника решается с помощью вспомогательной секущей проецирующей плоскости, проводимой через заданную прямую (рис.4.12).
Рис.4.12 Вспомогательная горизонтально проецирующая плоскость b(b`) проведена через прямую l.
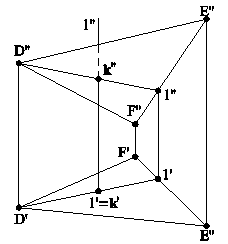
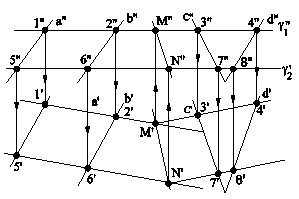
ПЕРЕСЕЧЕНИЕ МНОГОГРАННИКА ПЛОСКОСТЬЮ ОБЩЕГО ПОЛОЖЕНИЯ Задача на пересечение многогранника плоскостью общего положения решается с помощью вспомогательных секущих плоскостей в качестве “посредников”. На рис.4.12а приведен пример пересечения трехгранной призмы DEFD1E1F1 плоскостью треугольника АВС.
Рис.4.12а
Задача на рис.4.12а решена с помощью вспомогательных секущих плоскостей: a(a``), проведенной через сторону АВ треугольника АВС, которая пересекла призму по треугольнику 123, точки пересечения M и N c FD принадлежат искомой линии пересечения, и вспомогательных секущих плоскостей b(b`) и g(g``), с помощью которых найдены соответственно точки P и Q линии MPQN пересечения призмы DEFD1E1F1 c треугольником АВС. Определение видимости на чертеже не показано.
5. СПОСОБЫ ПРЕОБРАЗОВАНИЯ КОМПЛЕКСНОГО ЧЕРТЕЖА Рассматривая способы решения главных позиционных задач, следует отметить, что задачи двух первых типов решаются значительно проще, чем задачи третьего типа. В этой связи полезно отметить, что, зная способы преобразования комплексного чертежа, можно задачи третьего типа, при определенных условиях, преобразовать в задачи второго, которые решаются значительно проще. Под преобразованием комплексного чертежа понимают всякое построение на чертеже, отражающее определенное построение в пространстве и приводящее к образованию новых полей проекций. Принципиально имеют место два основных отличных друг от друга метода решения таких задач. С одной стороны, можно преобразовать чертеж: 1.Путем введения новых плоскостей проекций, а, с другой стороны, упрощение может быть достигнуто за счет перемещения заданных фигур путем преобразования движением: 2. Плоскопараллельным перемещением заданных геометрических образов и вращением их вокруг прямых частного положения в пространстве. Рассмотрим эти два метода.
5.1. СПОСОБ ВВЕДЕНИЯ НОВЫХ ПЛОСКОСТЕЙ ПРОЕКЦИЙ 1. Новая плоскость проекций должны быть перпендикулярной к одной из имеющихся плоскостей проекций. Любую, перпендикулярную к p1 или p2 плоскость, можно принять за новую плоскость проекций p3 или p4 (рис.5.1;5.2).
Рис.5.1 Рис.5.2
Этим способом можно решить четыре основные задачи на преобразование комплексного чертежа. Они следующие:
1. Задача на преобразование прямой общего положения в прямую уровня; 2. Задача на преобразование прямой общего положения в проецирующую прямую; 3. Задача на преобразование плоскости общего положения в проецирующую плоскость; 4. Задача на преобразование плоскости общего положения в плоскость уровня.
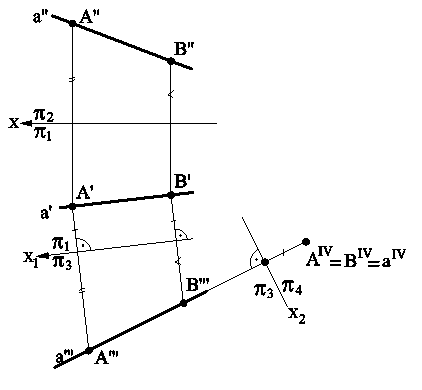
Рассмотрим эти задачи на примерах. 1. Преобразовать прямую а общего положения в прямую уровня. 2. Преобразовать прямую а общего положения в прямую проецирующую (рис.5.3). Решение: Выберем на прямой а две точки А и В и введем новую плоскость проекций p3, параллельную горизонтальной проекции этой прямой и перпендикулярно плоскости p1, и спроецируем прямую а (А,В) ортогонально на эту плоскость. Получим новую проекцию а "'(A"',B"'). Первая основная задача решена. Чтобы решить вторую основную задачу, продолжим построения дальше: Введем новую плоскость проекций p4, перпендикулярную проекцию а "' (A"',B"'). Эта плоскость пересечет p3 по оси х2. Спроецируем на новую плоскость нашу прямую а в точку а IV(AIV,BIV). Вторая основная задача решена. Она, как промежуточное построение, содержит первую основную задачу.
Рис.5.3
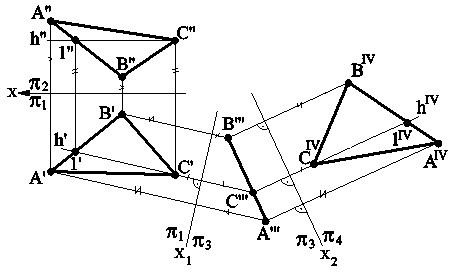
Рис.5.4
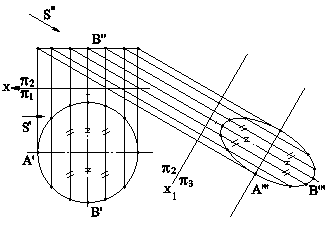
3. Преобразовать плоскость общего положения a (DАВС) в проецирующую плоскость; 4. Преобразовать плоскость общего положения a (DАВС) в плоскость уровня (рис.5.4). Решение: Проведем в плоскости треугольника АВС линию уровня, например, горизонталь h, и введем новую плоскость проекций p3, перпендикулярную этой линии уровня, и спроецируем на нее треугольник АВС. Получим прямую B"'C"'A"', в которую он выродится. Третья основная задача решена. Введем новую плоскость проекций p4, параллельную проекции B"'C"'A"'. Эта плоскость пересечет p3 по оси х2. Спроецируем на новую плоскость B"'C"'A"' и получим новую проекцию треугольника(AIV,BIV ,СIV), соответствующую натуральной величине треугольника АВС. 5.2. ПОСТРОЕНИЕ ИЗОБРАЖЕНИЙ ФИГУР ПО ЗАДАННОМУ НАПРАВЛЕНИЮ В машиностроительном черчении часто необходимо строить изображения заданных предметов или их частей по заданному направлению, указанному обычно стрелкой. Пример 1. Построить изображение окружности по стрелке s.(рис.5.5). Решение: Поскольку направление s параллельно фронтальной плоскости проекций, то новую плоскость проекций выбираем перпендикулярно направлению s`` и строим изображение этой фигуры на этой плоскости.
Рис.5.5 5.3. СПОСОБЫ ВРАЩЕНИЯ ВОКРУГ ПРЯМЫХ ЧАСТНОГО ПОЛОЖЕНИЯ К способам вращения вокруг прямых частного положения относятся способы вращения вокруг проецирующих прямых и прямых уровня. Последний способ называется способом совмещения.
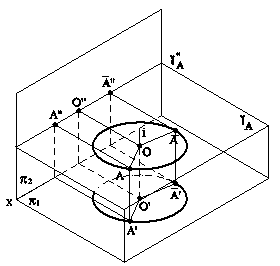
5.3.1. СПОСОБ ВРАЩЕНИЯ ВОКРУГ ПРОЕЦИРУЮЩИХ ПРЯМЫХ Если некоторая точка А вращается вокруг проецирующей прямой i, то она будет перемещаться по окружности, плоскость которой перпендикулярна оси вращения, а, следовательно проецироваться эта окружность на плоскость проекций, перпендикулярную оси вращения, будет без искажения (рис.5.7, 5.8).
Рис.5.7
Рис.5.8
Для решения четырех основных задач на преобразование комплексного чертежа выбор осей вращения осуществляется из соображений упрощения процесса преобразования.
Покажем это на примерах решения четырех основных задач. 1-я и 2-я основные задачи решены на рис.5.9. Чтобы преобразовать прямую l общего положения в прямую Для решения второй основной задачи продолжим построения и повернем нашу прямую 3-я и 4-я основные задачи решены на рис.5.10. Для преобразования плоскости a(DАВС) в проецирующую плоскость достаточно провести в плоскости линию уровня, например горизонталь С-1, а затем выбрать ось вращения i, перпендикулярную горизонтальной плоскости проекций и проходящую через горизонталь С-1, а затем выбрать ось вращения i, перпендикулярную горизонтальной плоскости проекций и повернуть горизонтальную проекцию треугольника АВС до положения, при котором горизонталь С-1 станет фронтально проецирующей прямой. Тогда плоскость a(DАВС) станет фронтально проецирующей плоскостью. 3-я основная задача решена. для решения 4-й основной задачи достаточно продолжить построения и повернуть плоскость треугольника АВС вокруг проецирующей прямой j так, чтобы она расположилась параллельно горизонтальной плоскости, плоскости p1. Четвертая задача на преобразование решена.
Рис.5.9
Рис.5.10
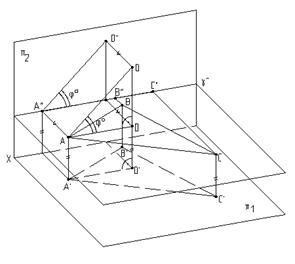
5.3.2. СПОСОБ ВРАЩЕНИЯ ВОКРУГ ЛИНИИ УРОВНЯ Способ вращения вокруг линий уровня используется в начертательной геометрии главным образом для определения натуральных величин плоских фигур. На рис.5.11 приведен пример определения натуральной величины треугольника АВС. Это решение равносильно решению четвертой основной задачи на преобразование комплексного чертежа и состоит в следующем: Во-первых, в плоскости заданного треугольника проводится линия уровня, например, фронталь, вокруг которой нужно повернуть заданную фигуру до положения, параллельного фронтальной плоскости проекций, или совместить эту фигуру с плоскостью j, проходящей через выбранную линию уровня - фронталь f.
Во-вторых, поворот можно осуществить преобразовав заданную плоскую фигуру - треугольник АВС - в проецирующую плоскость, введя дополнительную плоскость проекций p3, перпендикулярную фронтали f. Эта плоскость пересечет плоскость проекций p2 по оси х1. Проецируя треугольник АВС на эту плоскость, получим прямую А"'C"'B"'. Аналогично решению на рис.5.10, плоскость треугольника A"'C"'B"' можно преобразовать в плоскость уровня относительно фронтальной плоскости проекций p2, повернув вокруг фронтали f A"'C"'B"' до положения Но задача может быть решена без введения дополнительной плоскости проекций p3, так как натуральную величину радиуса вращения точки В можно определить с помощью способа прямоугольного треугольника. Его применение показано на исходном чертеже и дополнительного пояснения не требует.
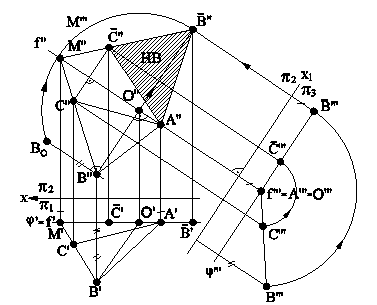
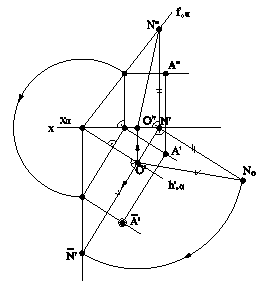
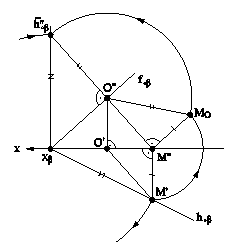
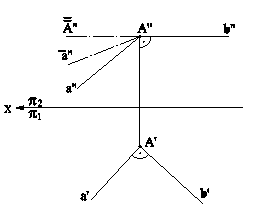
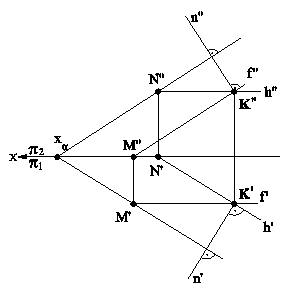
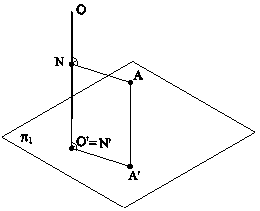
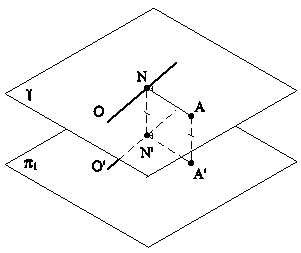
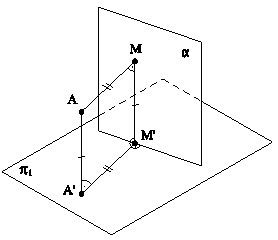
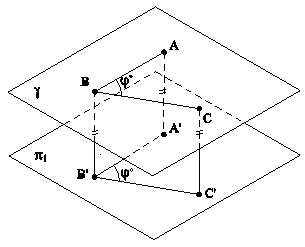
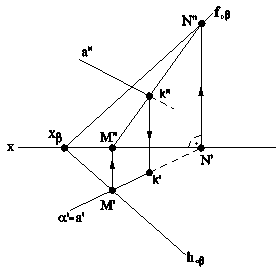
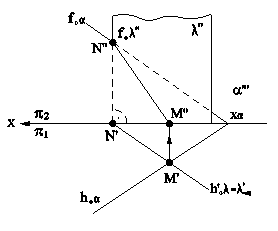
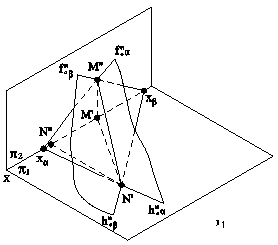
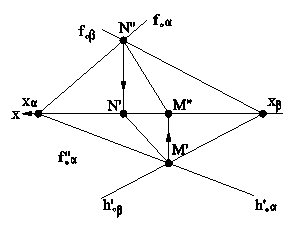
Рис.5.11 В случае задания плоскости ее следами, такую плоскость можно совместить с плоскостью проекций вращением вокруг соответствующего следа этой плоскости. На рис.5.12 плоскость a(h0a∩f0a), заданная следами, совмещена с горизонтальной плоскостью проекций. Для нахождения совмещенного положения плоскости на ее фронтальном следе выбрана произвольная точка N(N",N') и из нее опущен перпендикуляр NO(N"O",N'O') на горизонтальный след плоскости. Дальнейшее построение аналогично решению задачи на рис.5.11. При совмещении плоскости общего положения с плоскостью проекций может быть найдено совмещенное положение любой фигуры, принадлежащей этой плоскости, например, точки А. На рис.5.13 плоскость b(h0b∩f0b) cовмещена с плоскостью p2. Построения аналогичны и понятны из чертежа. При этом построении точка М(М",M') выбрана на горизонтальном следе плоскости, так как совмещение происходит путем вращения плоскости вокруг фронтального следа f0b плоскости b.
Рис.5.12
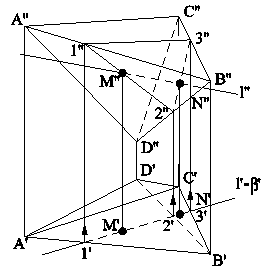
Рис.5.13
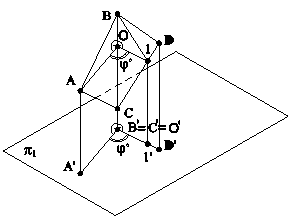
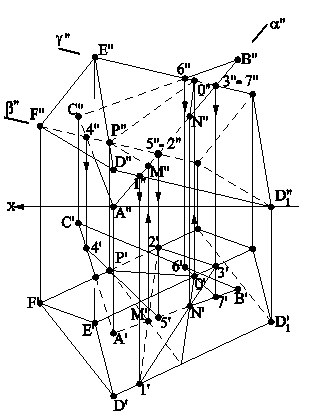
Рис.5.14 На рис.5.14 приведен пример совмещения тупоугольной плоскости l с горизонтальной плоскостью проекций. Совмещенное положение
Литература: Фролов С.А. Начертательная геометрия. М.: “Машиностроение”, 1983., гл.II, §§10,11,12. Гордон В.О. и др. Курс начерт. геом. Изд. “Наука”, М.: Глава V, §§ 34, 37. Локтев В.О. Краткий курс начерт.геом. М.: Гл.VII, §22.
5.4. CПОСОБ ПЛОСКОПАРАЛЛЕЛЬНОГО ПЕРЕМЕЩЕНИЯ (Способ вращения без указания оси поворота) Из планиметрии известно о преобразованиях “движение”, которые включают в себя ряд преобразований: параллельный перенос, вращение, преобразование симметрии и гомотетию. При этом одни преобразования могут быть заменены другими. Например, в случае параллельного переноса, а затем вращения отрезка, оба преобразования могут быть сведены к одному повороту, центр О вращения при этом может быть найден (рис.5.15, 5.16).
Рис.5.15(Параллельный перенос)
Рис.5.16 (Поворот)
Плоскопараллельный перенос фигуры в пространстве параллельно плоскости проекций, хотя и меняет положение фигуры, проекция этой фигуры на соответствующую плоскость проекций остается конгруэнтной (неизменной). Рассмотрим способ плоскопараллельного переноса на примере решения четырех основных задач на преобразование комплексного чертежа. 1-я и 2-я основные задачи (рис.5.17), 3-я и 4-я основные задачи (рис.5.18). Последовательность преобразования ясна из чертежей.
Рис.5.17
Рис.5.18 6. ВЗАИМНАЯ ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ Теоретической предпосылкой для построения на комплексном чертеже проекций прямых и плоскостей, перпендикулярных по отношению друг к другу в пространстве, служит свойство проекции прямого угла, одна из сторон которого параллельна какой-либо плоскости проекции: Если одна из сторон прямого угла параллельна плоскости проекции, то на данную плоскость прямой угол спроецируется прямым углом (рис.6.1, 6.2, 6.3).
Рис.6.1
Рис.6.2
Рис.6.3
6.1. ВЗАИМНАЯ ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ Для того чтобы прямая в пространстве была перпендикулярна плоскости, необходимо и достаточно, чтобы на чертеже горизонтальная проекция прямой была перпендикулярна к горизонтальной проекции горизонтали, а фронтальная проекция - к фронтальной проекции фронтали этой плоскости (правило 3ф, 3г) (рис.6.4, 6.5).
Рис.6.4
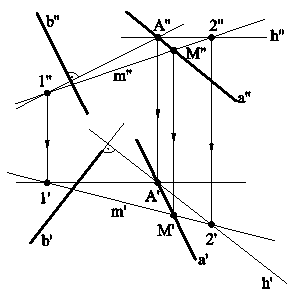
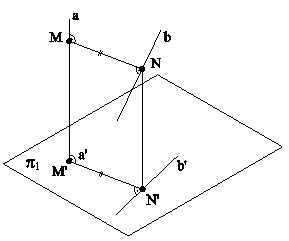
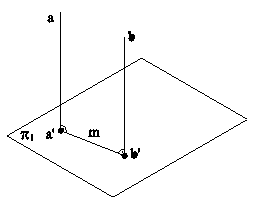
Рис.6.5 6.2. ВЗАИМНАЯ ПЕРПЕНДИКУЛЯРНОСТЬ ДВУХ ПРЯМЫХ ОБЩЕГО ПОЛОЖЕНИЯ В ПРОСТРАНСТВЕ Две прямые в пространстве будут взаимно перпендикулярными, если одна из них лежит в плоскости, перпендикулярной к другой прямой. Пример (рис.6.6). Найти горизонтальную проекцию прямой а, проходящей через точку А и перпендикулярную к прямой b.
Рис.6.6 Решение: Проведем через точку А плоскость a(h∩f), перпендикулярную заданной прямой b, так как любая прямая, лежащая в этой плоскости, будет перпендикулярна прямой b. С помощью вспомогательной прямой m найдем точку M', принадлежащую искомой прямой а, и проведем проекцию а' этой прямой.
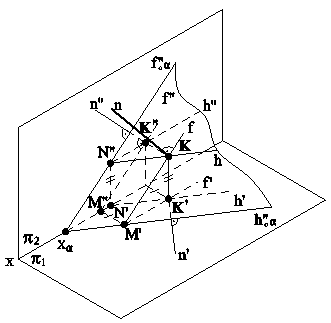
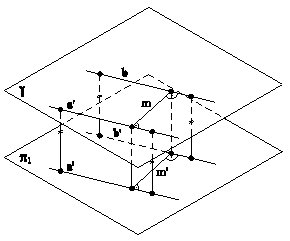
6.3. ВЗАИМНАЯ ПЕРПЕНДИКУЛЯРНОСТЬ ДВУХ ПЛОСКОСТЕЙ ОБЩЕГО ПОЛОЖЕНИЯ В ПРОСТРАНСТВЕ Две плоскости в пространстве будут взаимно перпендикулярными, если одна из них содержит прямую, перпендикулярную к другой плоскости. Пример (рис.6.7). Через прямую l провести плоскость l, перпендикулярную к заданной плоскости b(h∩f).
Рис.6.7 Решение: Через произвольную точку М на прямой l проведем прямую n, перпендикулярную к заданной плоскости b(h∩f). Условие перпендикулярности согласно п.6.1. Пересекающиеся прямые l и n, определят искомую плоскость l(n∩l).
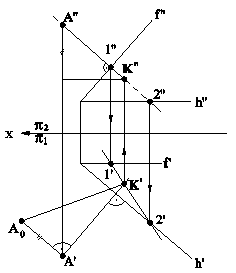
7. МЕТРИЧЕСКИЕ ЗАДАЧИ И СПОСОБЫ ИХ РЕШЕНИЯ Метрическими принято считать задачи, в условии или в решении которых присутствует численная характеристика. К метрическим задачам относятся задачи на построение изображений фигур по их размерам или координатам из точек, измерение расстояний, углов, площадей и другие. Метрические задачи бывают комплексными и включают в своем составе позиционные задачи. Из всего многообразия метрических задач выделяют две задачи, которые называются основными метрическими задачами. Первая задача - задача на перпендикулярность прямой линии и плоскости (п.6.1). Вторая основная задача - задача на измерение расстояния между двумя точками способом прямоугольного треугольника. Эти задачи называют основными потому, что на их основании можно решить любую другую метрическую задачу, то есть решение любой метрической задачи можно свести к решению основных метрических задач. Кроме этого, метрические задачи можно решать и способами преобразования комплексного чертежа. 7.1. РЕШЕНИЕ МЕТРИЧЕСКИХ ЗАДАЧ В ОБЩЕМ ВИДЕ Рассмотрим решение одной из метрических задач на примере, когда ее решение сводится к решению двух основных метрических задач. Пример (рис.7.1).Измерить расстояние от точки А до плоскости a(h∩f).
Рис.7.1
Решение: 1.Опустим из точки А перпендикуляр на плоскость a(h∩f) и найдем его основание - точку К. 2.Способом прямоугольного треугольника измерим истинную величину отрезка АК. Задача решена |АК|=А0K'.
7.2. РЕШЕНИЕ МЕТРИЧЕСКИХ ЗАДАЧ СПОСОБАМИ ПРЕОБРАЗОВАНИЯ КОМПЛЕКСНОГО ЧЕРТЕЖА Способами преобразования комплексного чертежа могут быть решены только те метрические задачи, которые имеют только один геометрический элемент, несущий на себе одну искомую численную характеристику. Алгоритм решения метрической задачи с помощью преобразования комплексного чертежа сводится к следующему: 1) определяется геометрический элемент оригинала, несущий на себе искомую численную характеристику и, 2) определяется “решающее положение” оригинала по отношению к плоскости проекций. (Решающим положением оригинала называют такое положение, при котором геометрический элемент, несущий на себе искомую численную характеристику, может быть спроецирован на плоскость проекций без искажений). Решающих положений может быть только четыре и им соответствуют и четыре известных задачи на преобразование комплексного чертежа.
7.3. ИЗМЕРЕНИЕ РАССТОЯНИЙ 1.Расстояние от точки до прямой измеряется длиной перпендикуляра, опущенного из точки на данную прямую. Это расстояние будет проецироваться на плоскость проекций без искажения в двух случаях: · когда прямая перпендикулярна плоскости проекций, то есть когда решена вторая задача на преобразование (рис.7.2); · когда прямая и точка расположены в плоскости, параллельной плоскости проекций, тоесть, когда решена четвертая основная задача (рис.7.3). 2.Расстояние между двумя скрещивающимися прямыми будет проецироваться на плоскость чертежа без искажения, когда одна из прямых займет положение, перпендикулярное к одной из плоскостей проекций, то есть когда будет решена вторая основная задача на преобразование (рис.7.4). 3.Расстояние между двумя параллельными прямыми спроецируется на плоскость проекций в истинную величину в двух случаях: · когда прямые расположатся перпендикулярно плоскости проекций; · будут лежать в плоскости, параллельной плоскости проекций, то есть когда будут решены соответственно вторая и четвертая основные задачи (рис.7.5 и 7.6). 4.Расстояние от точки до плоскости проецируется на плоскость проекций без искажения, когда заданная плоскость будет проецирующей по отношению к плоскости проекций, то есть будет решена третья основная задача на преобразование чертежа (рис.7.7).
Рис.7.2 Рис.7.3
Рис.7.4 Рис.7.5
Рис.7.6 Рис.7.7 7.4. ИЗМЕРЕНИЕ УГЛОВ 1. Угол между двумя пересекающимися прямыми спроецируется на плоскость проекций в истинную величину, когда обе его стороны будут лежать в плоскости, параллельной плоскости проекций, то есть когда будет решена четвертая основная задача. 2. Угол между двумя плоскостями измеряется линейным углом двугранного угла, то есть тогда, когда линия пересечения плоскостей будет перпендикулярна плоскости проекций. Это возможно, если решена вторая основная задача на преобразование. 3. Угол между прямой и плоскостью измеряется углом между прямой и ее проекцией на плоскость, то есть когда плоскость этого угла, расположится параллельно плоскости проекций, а это возможно в том случае, когда последовательными преобразованиями чертежа заданную плоскость сделать проецирующей, а прямую линию - линией уровня по отношению к этой плоскости проекций.
1. Плоский угол АВС=j0. 2. Двугранный угол j0ÐА01
Рис.7.8 Рис.7.9
3. Угол между прямой АD и плоскостью АВС=j0.
Рис.7.10 Примеры решения метрических задач 1. Определить расстояние от точки S до треугольника АВС (метод плоско-параллельного переноса)
Рис.7.11 2. Определить натуральную величину треугольника АВС (метод вращения вокруг прямой уровня).
Рис.7.12 3. Определить истинную величину ребра SC (в мм) и уголего наклона к плоскости треугольника АВС (в градусах).
Рис.7.13
|
|||||||||
|
Последнее изменение этой страницы: 2017-02-06; просмотров: 393; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.119.163 (0.015 с.) |







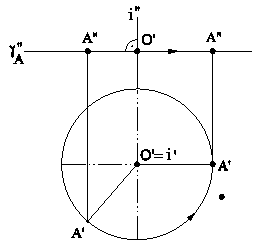
 уровня, достаточно выбрать на прямой д две точки, например, А и В, а затем через одну из них провести ось вращения. Если, к примеру, необходимо преобразовать прямую l (А,В) во фронтальную прямую
уровня, достаточно выбрать на прямой д две точки, например, А и В, а затем через одну из них провести ось вращения. Если, к примеру, необходимо преобразовать прямую l (А,В) во фронтальную прямую  , достаточно через одну из выбранных на этой линии точек провести горизонтально проецирующую прямую i, приняв ее за ось вращения, повернуть горизонтальную проекцию до положения
, достаточно через одну из выбранных на этой линии точек провести горизонтально проецирующую прямую i, приняв ее за ось вращения, повернуть горизонтальную проекцию до положения 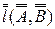 . Вторая основная задача решена.
. Вторая основная задача решена.
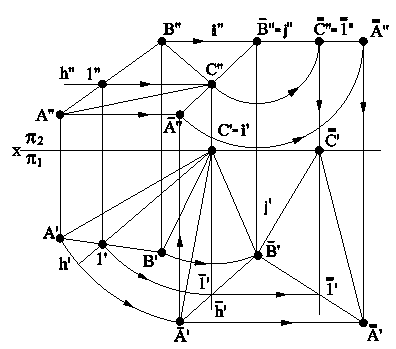
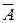 "'
"' 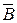 "'
"' 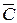 "'. При этом горизонтальная проекция треугольника
"'. При этом горизонтальная проекция треугольника