Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теплоотдача при вынужденном движении жидкостиСодержание книги
Поиск на нашем сайте
В ТРУБАХ И КАНАЛАХ Дано:
По трубке диаметром dвн и длиной l протекает вода со скоростью w. Определить коэффициент теплоотдачи, если средняя температура воды tж, средняя температура стенки tс. Как изменится значение коэффициента теплоотдачи, если диаметр трубы увеличить в 2 и 3 раза, сохраняя температуры и скорости движения постоянными? Построить график зависимости коэффициента теплоотдачи от диаметра трубки, α 1=ƒ(d).
Найти:
Δα -?
Решение: При экспериментальном изучении тепловых процессов принято выражать математическое описание процесса и расчетные уравнения в виде зависимостей между числами (критериями) подобия, представляющими собой безразмерные комплексы. Уравнения подобия, выражая обобщенную зависимость между величинами, характеризующими процесс, справедливы для всех подобных между собой процессов. Первая теорема подобия: для подобных между собой процессов Согласно второй теореме подобия связь между числами подобия выражается в форме однозначной функциональной зависимости, например N =f (Re, Рr, Gr). Третья теорема подобия утверждает, что условия подобия физических явлений, заключаются в подобии условий однозначности и равенстве одноименных чисел подобия, составленных из величин, входящих в эти условия. 6.1. Числа теплового и гидромеханического подобия процессов. Нуссельта число – безразмерный коэффициент теплоотдачи.
Где Средний коэффициент теплоотдачи в формуле (6.1.)
Относят к начальному температурному напору.
К среднеарифметическому напору
Или к среднелогарифмическому напору
Если
Прандтля число – безразмерная характеристика теплофизических свойств жидкости.
Где
Пекле число – критерий теплового подобия
Где Re – число Рейнольдса; Стантона число - критерий внутреннего конвективного переноса теплоты.
Фурье число – критерий тепловой гомохронности.
Где Био число – критерий краевого подобия
Тепловой критерий фазового перехода.
Где Галилея число – критерий подобия полей свободного течения.
Где Грасгофа число – критерий свободной тепловой конвекции
Где для капельных жидкостей приближенно Релея число – критерий теплообмена при свободной конвекции.
Фруда число – критерий гравитационного подобия, характеризует меру отношения сил инерции и тяжести в потоке.
Эйлера число – критерий подобия полей давления.
Где Архимеда число – критерий свободной конвекции.
Где Определяющая температура, по которой выбираются теплофизические свойства жидкости или газа, входящие в числа подобия, указывается нижним индексом возле числа подобия: «ж», «с», «п.с» - соответственно средняя температура жидкости, стенки, пограничного слоя. Определяющий геометрический размер также может быть указан нижним индексом возле числа подобия: l и h - длина и высота поверхности, d - диаметр трубы и т. п.
Решение задачи: Для средней температуры воды 10 0С берем из приложений: λ = 0,574 Вт/м*К кинематическая вязкость υ = 1,306*10-6 м2/с число Прандтля: Pr = 9,52 Определим режим течения жидкости:
При ламинарном режиме течения среднюю теплоотдачу рассчитываем по формуле:
Вычислим коэффициент теплоотдачи:
Увеличим диаметр трубы: d = 2dвн = 2*0,005 = 0,001 м Повторим расчеты: Определим режим течения жидкости:
При ламинарном режиме течения среднюю теплоотдачу рассчитываем по формуле:
Вычислим коэффициент теплоотдачи:
Увеличим диаметр трубы: d = 3dвн = 3*0,005 = 0,015 м Повторим расчеты: Определим режим течения жидкости:
При ламинарном режиме течения среднюю теплоотдачу рассчитываем по формуле:
Вычислим коэффициент теплоотдачи:
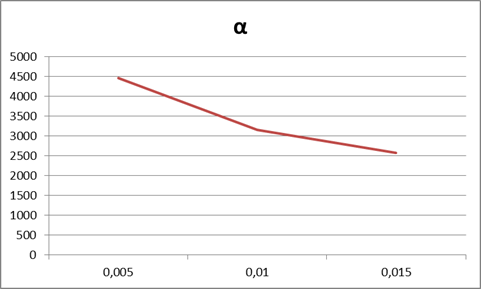
Из чего можно сделать вывод о том, что чем больше диаметр трубы, тем меньше коэффициент теплоотдачи. Отразим графически:
рис.1
Ответ: α1 = 4470 Вт/м2*с; α2 = 3161 Вт/м2*с; α3 = 2581 Вт/м2*с; Рис. 1
Задание № 7.10 (б)
|
|||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 358; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.32.238 (0.008 с.) |


 все одноименные числа подобия численно одинаковы.
все одноименные числа подобия численно одинаковы.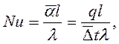 (6.1.)
(6.1.)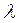 - теплопроводность жидкости;
- теплопроводность жидкости; 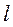 - характерный линейный размер.
- характерный линейный размер.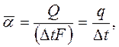
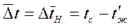 (6.2.)
(6.2.)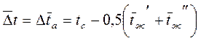 (6.3.)
(6.3.)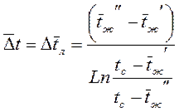 (6.4.)
(6.4.) Где
Где 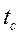 - средняя температура стенки,
- средняя температура стенки, 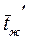 - температура набегающего потока или средне массовая температура на входе в трубу, в теплообменник,
- температура набегающего потока или средне массовая температура на входе в трубу, в теплообменник, 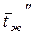 - средняя температура жидкости на выходе из трубы, теплообменника.
- средняя температура жидкости на выходе из трубы, теплообменника.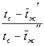 < 2, то вместо (6.4.) можно использовать (6.3.), т.е.
< 2, то вместо (6.4.) можно использовать (6.3.), т.е.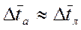 (5.5.)
(5.5.)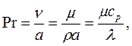 (6.6.)
(6.6.)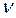 и
и 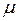 - кинематическая м2/с, и динамическая Па, вязкость.
- кинематическая м2/с, и динамическая Па, вязкость.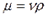 ;
; 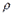 и
и 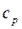 - площадь кг/м2 и изобарная массовая теплоемкость, Дж/(кг*К), жидкости;
- площадь кг/м2 и изобарная массовая теплоемкость, Дж/(кг*К), жидкости;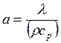 - температуропроводность жидкости м2/с.
- температуропроводность жидкости м2/с.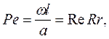 (6.7.)
(6.7.)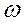 - характерная скорость потока, м/с.
- характерная скорость потока, м/с.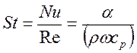 (6.8.)
(6.8.)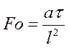 (6.9.)
(6.9.)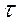 - время протекания нестационарного процесса теплопроводности.
- время протекания нестационарного процесса теплопроводности.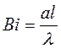 (6.10.)
(6.10.) Где
Где  - характерный линейный размер твердого тела,
- характерный линейный размер твердого тела, 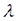 - теплопроводность твердого тела.
- теплопроводность твердого тела.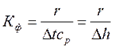 (6.11.)
(6.11.)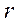 - теплота испарения (конденсата), Дж/кг,
- теплота испарения (конденсата), Дж/кг, 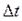 - разность температур насыщения и перегрева (переохлаждения) фазы,
- разность температур насыщения и перегрева (переохлаждения) фазы, 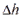 - разность энтальпий фазы в состояниях насыщения и перегрева (переохлаждения).
- разность энтальпий фазы в состояниях насыщения и перегрева (переохлаждения).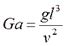 (6.12.)
(6.12.)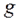 - ускорение свободного падения м/с2
- ускорение свободного падения м/с2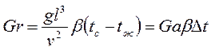 (6.13.)
(6.13.)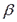 - коэффициент объемного расширения, К-1, для идеальных газов
- коэффициент объемного расширения, К-1, для идеальных газов 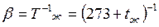 ;
;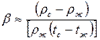 ; где
; где 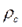 и
и 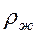 - плотность жидкости при
- плотность жидкости при 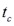 и
и 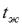 .
.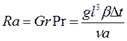 (6.14.)
(6.14.)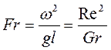 (6.15.)
(6.15.) Рейнольдса число – критерий режима движения жидкости.
Рейнольдса число – критерий режима движения жидкости.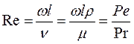 (6.16.)
(6.16.)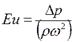 (6.17.)
(6.17.)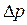 - перепад давления на участке движения жидкости.
- перепад давления на участке движения жидкости.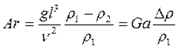 (6.18.)
(6.18.)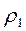 и
и 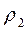 - плотность жидкости в двух точках потока.
- плотность жидкости в двух точках потока.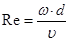
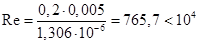 => Ламинарный режим
=> Ламинарный режим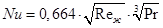
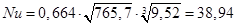

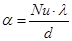
 Вт/(м2∙ ̊ С)
Вт/(м2∙ ̊ С)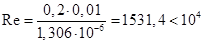 => Ламинарный режим
=> Ламинарный режим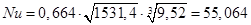
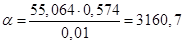 Вт/(м2∙ ̊ С)
Вт/(м2∙ ̊ С)
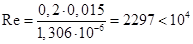 => Ламинарный режим
=> Ламинарный режим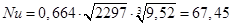
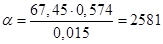 Вт/(м2∙ ̊ С)
Вт/(м2∙ ̊ С)