
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теплопроводность при наличии внутреннихСодержание книги
Поиск на нашем сайте
Источников теплоты
Дано: Электропривод диаметром d покрыт изоляцией толщиной δ. По проводу проходит ток силой I. Температура окружающего воздуха tв, а коэффициент теплоотдачи к воздуху α. Найти температуру на оси провода, а также на поверхности провода и изоляции и построить температурный график.
Найти:
t оси, tпов, tиз –?
Решение:
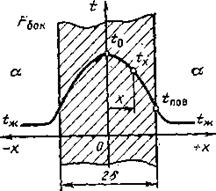
Рассмотрим однородную плоскую стенку толщиной 2δ, коэффициент теплопроводности λ которой постоянен. Внутри этой стенки имеются равномерно распределённые источники теплоты qv. Выделившаяся теплота через боковые поверхности стенки передаётся в окружающую среду. Для плоской пластины (λ=const), равномерно охлаждаемой c обеих сторон (рис. 3.1), задана температура поверхности t пов.
рис. 3.1 - Одномерное температурное поле в пластине толщиной 2δ
где В формуле (4.1) при х = 0 температура в середине толщины пластины
Учитывая зависимость
Для плоской пластины (λ=const), равномерно охлаждаемой с обеих сторон, заданы температура среды tЖ и коэффициент теплоотдачи α. Одномерное температурное поле в пластине
где при х=0 температура в середине толщины пластины
Мощность внутренних источников теплоты для пластины определяются по формулам:
Связь между объемной qv и поверхностной qF плотностями тепловыделения используется при определении теплового потока на боковых поверхностях пластины
4.2. Цилиндрический стержень Для бесконечного стержня (λ=const) задана температура на оси tоси. Температурное поле в стержне диаметром d0
где В формуле (4.8) при
С учетом зависимости
Для стержня (λ=const), равномерно охлаждаемого средой, заданы ее температура tж и коэффициент теплоотдачи α. Температурное поле в стержне
В формуле (4.14): при dx=0 температура на оси стержня
при dx = d0 температура на поверхности стержня
Мощность внутренних источников теплоты для стержня
4.3. Цилиндрическая труба Теплота отводится через внешнюю поверхность трубы. Температурное поле в стенке трубы с внутренним радиусом r1 и внешним r2
где r1 ≤ r x≤ r2; t1 - температура на внутренней теплоизолированной поверхности трубы. Подставляя в формулу (4.20) rх = r2, можно получить расчетное выражение для перепада температуры в стенке
и формулу для линейной плотности теплового потока
где t2 - температура на внешней поверхности трубы. Теплота отводится через внутреннюю поверхность трубы.
Перепад температур в стенке
Линейная плотность теплового потока.
Теплота отводится через обе поверхности трубы. Перепад температур в стенке
где r0 - радиус поверхности, которая имеет наибольшую температур to, r1<r0<r2. Этот радиус определяется из зависимости
Наибольшую температуру в стенке трубы можно найти по выражению
Или 4.4. Теплообмен в условиях электрического нагрева. При прохождении электрического тока по проводнику цилиндрической формы диаметром dц и длиной l температуры рассчитываются формулам (4.12) и (4.15), в которых qv выражается через электрические параметры: I -
Где
Решение задачи: Из приложений учебников находим: Коэффициент теплопроводности винипласта: λв = 0,13 Вт/(м*К) удельное улектроспротивление меди:
Вычислим тепловой поток на метр провода:
Найдем искомые температуры: На поверхности изоляции:
На поверхности провода:
На оси провода:
Ответ:
|
|||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 633; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.26.231 (0.01 с.) |


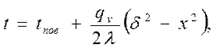 (4.1)
(4.1)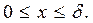
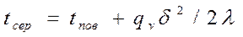 (4.2)
(4.2)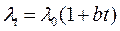 в условиях больших перепадов температур, температурное поле в пластине можно рассчитать по формуле
в условиях больших перепадов температур, температурное поле в пластине можно рассчитать по формуле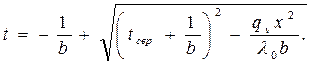 (4.3)
(4.3)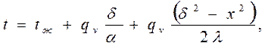 (4.4)
(4.4)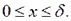
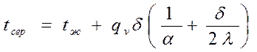 (4.6)
(4.6)
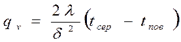 ; (4.7)
; (4.7)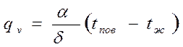 ; (4.8)
; (4.8)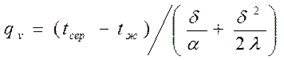 . (4.9)
. (4.9)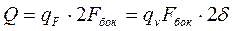 ;
; 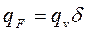 (4.10)
(4.10)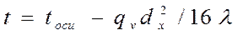 , (4.11)
, (4.11)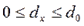 .
.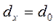 температура на поверхности стержня
температура на поверхности стержня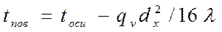 . (4.12)
. (4.12)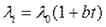 температурное поле в стержне
температурное поле в стержне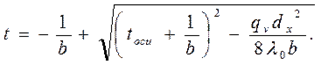 (4.13)
(4.13)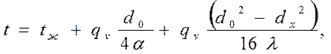 (4.14)
(4.14)
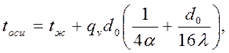 (4.15)
(4.15)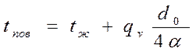 . (4.16)
. (4.16)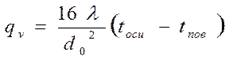 ; (4.17)
; (4.17)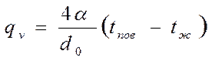 ; (4.18)
; (4.18) . (4.19)
. (4.19)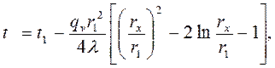 (4.20)
(4.20)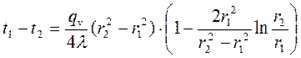 (4.21)
(4.21)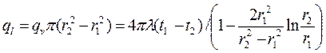 , (4.22)
, (4.22) Температурное поле в стенке трубы
Температурное поле в стенке трубы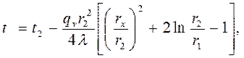 (4.23)
(4.23)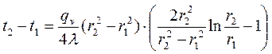 (4.25)
(4.25)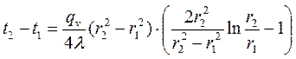 (4.26)
(4.26)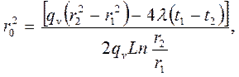 (4.27)
(4.27)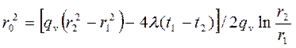 (4.28)
(4.28)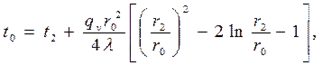
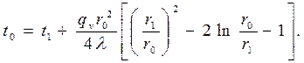 (4.28)
(4.28) силу тока, A; U - напряжение, В; Rэл - электрическое сопротивление проводника, Ом:
силу тока, A; U - напряжение, В; Rэл - электрическое сопротивление проводника, Ом: (4.29)
(4.29)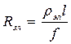 ;
; 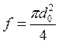 ;
; 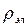 - удельное электрическое сопротивление материала проводка Ом*м.
- удельное электрическое сопротивление материала проводка Ом*м.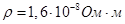
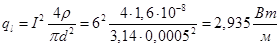
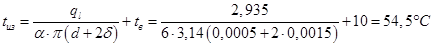

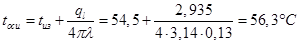
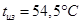 ,
, 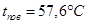 ,
, 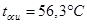
 Задание № 5.9 (б)
Задание № 5.9 (б)


