
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теплопроводность при нестационарном режимеСодержание книги
Поиск на нашем сайте
Дано: Труба с водой находиться в среде с температурой tж. Внезапно температура среды понижается до tж 1. Подсчитать, через сколько времени вода в трубе начнет замерзать, диаметр трубы dн ´δ. Коэффициент теплоотдачи от трубы к среде α. Расчет произвести, не учитывая теплоинерционные свойства металла трубы.
Найти: Δt –?
Решение: Нестационарная теплопроводность характеризуется изменением температурного поля тела во времени и связана с изменением энтальпии тела при его нагреве или охлаждении. Безразмерная температура тела θ определяется с помощью числа Био Вi = аl/λ, числа Фурье Fo = aτ/l2 и безразмерной координаты, обозначаемой для пластины, X = x/δ, а для цилиндра R = r/ro. Охлаждение (нагревание) тел поисходит в среде с постоянной температурой tж, при постоянном коэффициенте теплоотдачи α; λ и а - теплопроводность и температуропроводность материала тела, l - характерный размер тела (l = δ для пластины, l=r0 для цилиндра), х и r - текущие координаты соответственно для пластины и цилиндра. 5.1. Тепа с одномерным температурным полем. Пластина толщиной 2δ. Безразмерная температура пластины
где t - температура в пластине для момента времени т в точке с координатой х; t0 - температура пластины в начальный момент времени. Если Fo ≥ 0,3 то температура на поверхности пластины (Х=1)
температура на середине толщины пластины (Х=0)
температура внутри пластины на расстоянии х от ее средней плоскости
где P, N, μ1, μ12 определяются по табл. 5 приложения для пластины в зависимости от числа Bi. Температура Цилиндр радиусом r0. Безразмерная температура цилиндра
где t - искомая температура в цилиндре для радиуса rх и времени τ, 0≥ rх ≤ r Если Fo ≥ 0,3 то температура на поверхности пластины (R=1)
температура на оси цилиндра (R=0)
температура внутри цилиндра для радиуса rх
где P0, N0, μ1, μ12 определяются по табл. 6 приложения для цилиндра в зависимости от числа Bi; Температуры
5.2. Тела конечных размеров. Температура определяется на основе теоремы о перемножении решений: безразмерная температура тела конечных размеров при нагревании (охлаждении) равна произведению безразмерных температур тел с бесконечным размером, при пересечении которых образовано данное конечное тело. Цилиндр длиной 2δ и радиусом r0 (рис. 4.1). Он образован пересечением бесконечной пластины толщиной 2δ и бесконечного цилиндра радиусом r0. Безразмерная температуры стержня
При Fo ≥ 0,3 безразмерная температура внутри цилиндрического стержня в точке с координатами х и rх будет определяться аналогично, но
Решение задачи: По условию задачи сказано, что не учитываем теплоинерционные свойства металла трубы. Значит, расчет проводим для воды. Исходная температура – t0 = 10 0С По таблицам приложений находим: λводы = 0,574 Вт/(м·К) По известным значениям радиуса и коэффициента α найдем значения критерия Био Диаметр воды – это диаметр трубы минус толщина = 90 – 2 = 88 мм Соответственно радиус = d/2 = 88/2 = 44 мм = 0,044 м
Из приложения П.16 находим μ1 = 1,7234 и D1 = 1,392 В заданный момент безразмерная температура в центре трубы:
Так же
В таблицах приложений нет значений ε для Bi = 2,64 Решим это уравнение в системе МатКАД, получим: ε1 = 1,16; R = r/r0 = 1; Тогда по таблицам находим J0 = J0(1,2) = 0,6711 Получим:
Так же число Фурье можно найти и по другой формуле:
Откуда: а – коэффициент температуропроводности (м2/с)
Из таблиц приложений для воды (при t = 10 0С) берем данные и вычисляем:
Находим время охлаждения воды до 0 0С:
Ответ: τ = 1,8 ч. Задание № 6.4 (б)
|
|||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 667; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.155.253 (0.01 с.) |

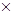 2
2

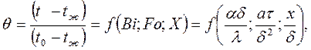 (5.1)
(5.1)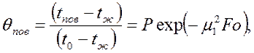 (5.2)
(5.2)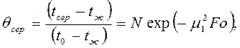 (5.3)
(5.3)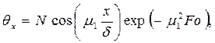 (5.4)
(5.4)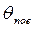 и
и 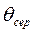 можно определить по графикам рис. П.1 и П.2 по известным числам Bi и Fo.
можно определить по графикам рис. П.1 и П.2 по известным числам Bi и Fo.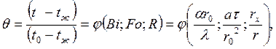 (5.5)
(5.5)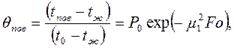 (5.6)
(5.6)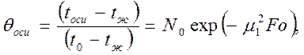 (5.7)
(5.7)
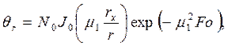 (5.8)
(5.8)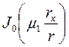 - функция Бесселя первого рода нулевого порядка (табл. 19 приложения).
- функция Бесселя первого рода нулевого порядка (табл. 19 приложения).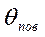 и
и 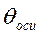 можно определить по графикам рис. П.З и П. 4 Приложения по известным числам Bi и Fo
можно определить по графикам рис. П.З и П. 4 Приложения по известным числам Bi и Fo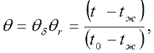 равна
равна 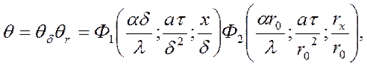 (5.9)
(5.9)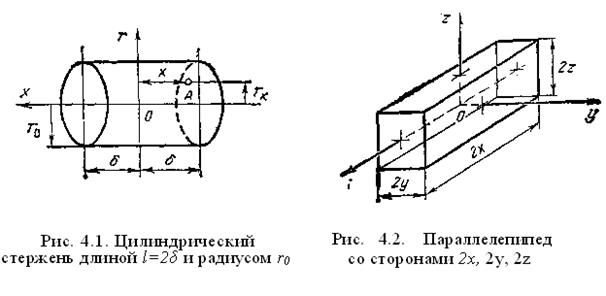
 где
где 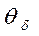 (или функция Ф1) при Fo ≥ 0,3 определяется по формулам (5.1) - (5.3) и графикам рис. П.1 и П.2 приложения для бесконечной пластины толщиной 2δ;
(или функция Ф1) при Fo ≥ 0,3 определяется по формулам (5.1) - (5.3) и графикам рис. П.1 и П.2 приложения для бесконечной пластины толщиной 2δ; 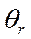 (или функция Ф2) при Fo ≥ 0,3 определяется по формулам (5.5) - (5.7) и графикам рис. П.З и П.4 приложения для бесконечного цилиндрического стержня радиусом r0.
(или функция Ф2) при Fo ≥ 0,3 определяется по формулам (5.5) - (5.7) и графикам рис. П.З и П.4 приложения для бесконечного цилиндрического стержня радиусом r0.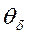 рассчитывается по формуле (5.4), a
рассчитывается по формуле (5.4), a 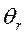 - по формуле (5.8) с использованием табл. 5 и 6 приложения.
- по формуле (5.8) с использованием табл. 5 и 6 приложения.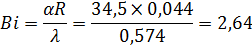
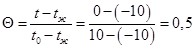
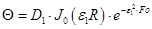
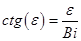
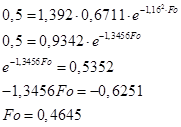

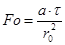
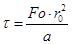
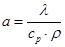
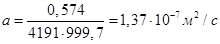
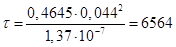 с или 109,4 минут или 1,8 часа
с или 109,4 минут или 1,8 часа


