
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Выбор гидроаппаратуры, их технические характеристики
Выбор распределителей. Гидрораспределители предназначены для изменения направления или пуска и остановки потока в двух или более линиях в зависимости от наличия внешнего управляющего воздействия. Они позволяют реверсировать движение рабочих органов в станках, останавливать рабочие органы, а также выполнять другие операции в соответствии с гидросхемой распределителя. Распределители имеют запорно регулирующий элемент, выполненный в виде золотника, совершающего осевое движение. Выбираем ПГ73-35: Основные параметры: ¾ Расход масла: номинальный: 2000л/мин; максимальный: 3200л/мин; ¾ Масса: 40кг. ¾ Рабочее давление 35 МПа. Выбор предохранительного клапана Предохранительные клапаны предназначены для предохранения гидропривода от давления, превышающего установленное. Они действуют эпизодически лишь в аварийных режимах работы гидропривода (пропускают масло из напорной линии в сливную) в отличие от переливных клапанов, предназначенных для поддержания заданного давления путем непрерывного слива масла во время работы. предохранительные клапаны станочных гидросистем, как правило, работают в режиме переливных клапанов. Выбираем: МКПВ32,3…2 Основные параметры: ¾ Давление: 2-25МПа; ¾ Диаметр условного прохода: 32 мм; ¾ Номинальный расход масла: 320л/мин; ¾ Масса: 10 кг.
Разработка гидравлического источника питания Источником питания гидропривода холодильника МНЛЗ служит насосно аккумуляторная станция (Рисунок 13), которая состоит из следующих элементов: - шести аксиально роторно-поршневых насосов (4 рабочих, 2 резервных) с параметрами: Q= 350 л/мин – подача; N=90 кВТ – мощность; n=1500 об/мин; pmax=250 Бар=25 МПа pн=160 Бар=16 МПа. - бака с маслом, объемом 10000 литров, - восьми пневмогидравлических аккумуляторов, закаченных азотом (также, любым инертным газом) типа АРФ 16/320. Объем аккумулятора, необходимый для перемещения заготовки от одного края на другой – Vакк=0,46м3, - станции рециркуляции масла (фильтрация охлаждение) для поддержки рабочей температуры и чистоты масла. В нее входят: · 2 насоса винтовых для забора масла с бака Q=450 л/мин, pmax=1 МПа; · 2 напорных фильтра, чистота очистки 5 мкм. С насосной установки жидкость под давлением 16 МПа идет на аккумуляторы и на столы управления. При срабатывании гидроцилиндра холодильника, работающего на подъем, при недостаточном расходе рабочей жидкости от насосов, начинают работать аккумуляторы, дополняя нужный расход гидросистеме, далее при разрядке аккумуляторов снова начинается их заправка. При отключении насосов на аккумуляторах можно аварийно закончить цикл.
Для очистки рабочей жидкости и поддержании ее в рабочем состоянии в системе находится станция рециркуляции, которая фильтрует и охлаждает рабочую жидкость, что позволяет существенно улучшить рабочий процесс и уменьшить расход рабочий жидкости.
Рисунок 13 – Гидросхема насосно-аккумуляторной станции
Оценка волновых процессов Привод холодильников шагового типа работает в тяжёлом повторно-кратковременном режиме со ступенчато прикладываемой к нему внешней нагрузкой. Цикл работы привода представляет собой определённую последовательность работы цилиндров подъёма и цилиндров перемещения Гидроцилиндры, работающие на подъем, ход поршня у которых 250мм, поднимают заготовки (две плавки) весом 698тонн плюс вес рамы 300тонн со скоростью 50мм/сек.. Действие продолжается 4 ÷ 6 сек, после чего срабатывают гидроцилиндры, работающие на перемещение, со скоростью 75мм/сек и продвигают заготовки на 300мм за время равное 9 ÷ 10 секундам. После того, как гидроцилиндры перемещения продвинули заготовки, они возвращаются в исходное положение, за тем гидроцилиндры подъема опускаются, держа на себе лишь вес рамы. Цикл повторяется. Все время цикла занимает 19 ÷ 20 секунд При рассмотрении продольных колебаний жидкости в трубопроводе, воспользуемся гипотезой пренебрежения поперечными движениями частиц жидкости, уравнение движения в этом случае выглядит следующим образом: [22, с. 325]
где x— перемещение поперечного сечения, начальное положение которого характеризуется координатой z. Рассмотрим решение уравнения (73) по методу Даламбера. Легко видеть, что выражение: [22, с. 325]
всегда является решением уравнения, каковы бы ни были функции
(77) где штрихи означают дифференцирование функций Подставляя выражение (76) в уравнение (74), видим, что оно удовлетворяется тождественно. Таким образом, выражение (75) действительно является решением уравнения (74) и притом решением общим, так как оно содержит две произвольные функции. Физический смысл выражения (75) очевиден. Первое слагаемое т. е. для наблюдателя, движущегося вдоль стержня со скоростью Рассмотрим задачу об ударе жесткого груза по столбу жидкости, конец которого будем считать «заделанным» (рисунок 14).
Рисунок 14 - удар груза о столб жидкости
Предполагается, что после соприкосновения груз и столб жидкости представляют собой одно целое до тех пор, пока усилие их взаимодействия остается сжимающим. Поместим начало координат в точку удара. Тогда для правого конца столба
Так как в этом равенстве
где аргумент Если произвести соответствующую замену в выражении (75), то
Вид функции Считая, что груз движется вместе с концом стержня
Эта сила уравновешивается продольной силой на конце стержня, равной
Таким образом, уравнение движения груза имеет вид: [22, с. 326]
(83) или, поскольку
где x - отношение массы столба жидкости к массе груза, ........ Подставляя в уравнение (78) вместо
где штрихи обозначают дифференцирование по аргументу. Отсюда:
Дифференциальное уравнение (82) связывает значения функции До соприкосновения груза т со столбом жидкости (т.е. при
Интегрируя это уравнение, находим, что при
Так как в начальный Момент Таким образом, при
Зная функцию При
соответственно скорости и деформации в любом сечении равны:
Подставляя сюда значение
Рисунок 15 – Графики скоростей и деформаций
Пока волна деформации не дошла до опоры, скорости и деформации в любом сечении оказываются связанными простым соотношением
Таким образом, давление, возникающее в стержне в первый момент удара, полностью определяется скоростью удара и не зависит от массы ударяющего груза. Выше рассмотрен лишь первый этап удара, когда имеется только прямая волна деформации, идущая по стержню слева направо. Уравнение (20) позволяет построить функцию
Произвольная постоянная при интегрировании этого уравнения определяется из условия, что скорость груза, а значит, и скорость конца стержня
представляет собой непрерывную функцию. Это условие удовлетворяется, если разрывы функции
должна увеличиваться до
Последнее значение
Аналогично находим при
Таким образом, шаг за шагом можно сконструировать функцию Далее, можно интегрированием получить функцию при
при
при
и т.д. Зная функцию
Рисунок 16- график давлений
Таким образом, произведён расчёт волнового процесса от одного удара, определяющийся скоростью ударяемых тел, то есть разностью скоростей подвижных балок и груза. Но результат решения динамической задачи о движении балок и груза даёт нам целую серию ударов, происходящих один за другим с разными скоростями взаимодействия, следовательно наложение волн в этом случае будет происходить не только от первого удара заготовок в момент начала их движения прямых и отражённых, но и прямых и отражённых волн от последующей серии ударов.
Организационная часть
|
||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 456; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.65.65 (0.045 с.) |

 , (74)
, (74) (75)
(75) и
и  . Вычисляя производные от выражения (74), находим:
. Вычисляя производные от выражения (74), находим: (76)
(76) и
и  по аргументам.
по аргументам. представляет волну давления, движущуюся вдоль стержня в направлении оси
представляет волну давления, движущуюся вдоль стержня в направлении оси  со скоростью
со скоростью  . Действительно, при
. Действительно, при  ,
, , картина давлений, соответствующих функции
, картина давлений, соответствующих функции  остается неизменной. Точно так же второе слагаемое представляет волну давлений, движущуюся с той же скоростью в противоположном направлении. Движение стержня можно рассматривать как результат сложениядвух волн давлений, движущихся в противоположных направлениях. Задача заключается в выборе вида функций
остается неизменной. Точно так же второе слагаемое представляет волну давлений, движущуюся с той же скоростью в противоположном направлении. Движение стержня можно рассматривать как результат сложениядвух волн давлений, движущихся в противоположных направлениях. Задача заключается в выборе вида функций  и
и  так, чтобы выполнялись начальные и граничные условия. Эта задача может быть решена в каждом частном случае.
так, чтобы выполнялись начальные и граничные условия. Эта задача может быть решена в каждом частном случае.
 получим граничное условие
получим граничное условие  . Подставив сюда вместо х выражение (75), найдем: [22, с. 325]
. Подставив сюда вместо х выражение (75), найдем: [22, с. 325] (78)
(78) может принять любое значение, то
может принять любое значение, то , (79)
, (79) может принимать произвольные значения.
может принимать произвольные значения. , (80)
, (80) можно определить, рассматривая взаимодействие столба жидкости с грузом.
можно определить, рассматривая взаимодействие столба жидкости с грузом. , находим его силу инерции:
, находим его силу инерции: , (81)
, (81) , (82)
, (82)
 ,
, , (84)
, (84) , (85)
, (85) его значение из выражения (75) и заменяя буквой
его значение из выражения (75) и заменяя буквой  величину
величину  , получаем: [22, с. 326]
, получаем: [22, с. 326] , (86)
, (86) , (87)
, (87) со значением этой функции для аргумента, меньшего на
со значением этой функции для аргумента, меньшего на  . Используя формулу (82) и начальные условия, можно шаг за шагом построить функцию
. Используя формулу (82) и начальные условия, можно шаг за шагом построить функцию  ) для всех точек жидкости смещение равно нулю. Следовательно, при
) для всех точек жидкости смещение равно нулю. Следовательно, при  . Поэтому для интервала
. Поэтому для интервала  правая часть уравнения (82) равна нулю:
правая часть уравнения (82) равна нулю: , (88)
, (88)
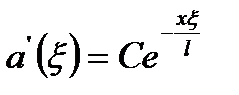 , (89)
, (89) скорость конца столба жидкости
скорость конца столба жидкости 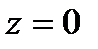 равна скорости груза
равна скорости груза  , то
, то  . Подставляя сюда выражение, получаем
. Подставляя сюда выражение, получаем  , или, так
, или, так  .
. функция
функция  определяется выражением: [22, с. 326]
определяется выражением: [22, с. 326] (90)
(90) , можно исследовать изменение усилий и скоростей в любом сечении стержня, начиная с первого момента удара и до тех пор, пока
, можно исследовать изменение усилий и скоростей в любом сечении стержня, начиная с первого момента удара и до тех пор, пока  , т.е. пока до данного сечения не дойдет отраженная от опоры волна деформации.
, т.е. пока до данного сечения не дойдет отраженная от опоры волна деформации. функция
функция  и выражение для перемещения имеет вид
и выражение для перемещения имеет вид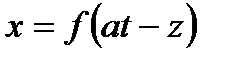
 , (91)
, (91) по формуле (83), найдем, что при
по формуле (83), найдем, что при 
 (92)
(92) , а деформация — от нуля до
, а деформация — от нуля до  .
.
 , (93)
, (93) . Подставив в правую часть этого уравнения найденное выше значение функции
. Подставив в правую часть этого уравнения найденное выше значение функции  , (94)
, (94) не могут изменяться скачкообразно, т. е. что
не могут изменяться скачкообразно, т. е. что , (95)
, (95) . Так как при
. Так как при  функция
функция  , то этот же скачок повторяется и при
, то этот же скачок повторяется и при  и т. д. В частности, при
и т. д. В частности, при  функция
функция  , (96)
, (96) , (97)
, (97) , (98)
, (98)
 ,
,  (99)
(99) , которая является непрерывной:
, которая является непрерывной: , (100)
, (100) , (101)
, (101)
 , (102)
, (102) . Продифференцировав по
. Продифференцировав по  , находим деформацию
, находим деформацию  :
: , (103)
, (103)



