
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Стереометрія. Сторінки історіїСтр 1 из 10Следующая ⇒
Стереометрія. Сторінки історії Зміст Декілька штрихів до «портрета» геометрії……………………………………...3 Геродот і Арістотель про походження геометрії………………………………..5 Платон і Арістотель про зміст геометрії…………………………………….…..6 Фалес та ідея логічного обґрунтування у геометрії………………………….....9 Архімед…………………………………………………………………………...12 Піфагор і піфагорійці…………………………………………….……………...13 Евклід і його «Начала»…………………………………………………………..18 «Начала» Евкліда і проблема паралельних прямих…………………………...22 Кутомірні інструменти………………………………………………………......28 З історії теореми про три перпендикуляри………………………………...…..30 Обчислення об'єму піраміди: з імли століть……………………………….…..31 «Кубок Кеплера»……………………………………………………...…………37 Кавальєрі…………………………………………………………...…………….39 Як Блез Паскаль став геометром………………………………….…………….41 Феофан Прокопович………………………………………………….………….43 Леонард Ейлер………………………………………………...…………………45 Микола Іванович Лобачевский…………………………………….…………...46 Михайло Васильович Остроградський……………………………………..…..48 Рекомендована література………………………………………………………50 Геродот і Арістотель про походження геометрії Слово «геометрія» утворене від двох давньогрецьких слів «гео» — земля і «метрео» — вимірюю, отже, дослівно означає «землемірство». (Корінь «гео» входить до складу назв й інших наук, як-от: географія, геологія, геодезія, геомеханіка, геофізика, геохімія тощо). Про походження геометрії «батько історії» Геродот у V ст. до н.е. дослівно писав так: «Єгипетські жерці говорили, що цар Сесотріс розділив землю між усіма єгиптянами, давши кожному по прямокутній ділянці; з цього він почав отримувати дохід, наказавши щорічно сплачувати податок. Якщо ж від якої-небудь ділянки Ніл відрізав якусь частину, то власник, приходячи до царя, сповіщав про цю пригоду. Цар же посилав людей, які повинні були обстежити ділянку землі і виміряти, наскільки меншою вона стала, щоб власник сплачував податок з решти площі, пропорційно до встановленого. Мені здається, що саме так було винайдено геометрію, яка потім з Єгипту була перенесена в Елладу».
Отже, Геродот пов'язував походження геометрії з практичними потребами людини, а саме — з вимірюванням і межуванням земель. Через два століття після Геродота енциклопедист античного світу Арістотель висловив зовсім іншу думку про походження геометрії. Основне джерело виникнення цієї науки він вбачав у вільній розумовій діяльності наділених дозвіллям людей: «Математичне мистецтво найперше було створене в Єгипті, оскільки там жерці мали час для дозвілля». Одначе істина, мабуть, поєднує обидва ці припущення. Вочевидь важливими були і практичні потреби, і вільна розумова діяльність. Від прадавньої єгипетської епохи до нас дійшли лише дві цілісні математичні пам'ятки. Це записані на папірусі збірники задач із розв'язаннями. Глибоко символічним є початок і закінчення папірусного тексту, автор якого називає себе писарем Ахмесом. Перша фраза є своєрідним пророцтвом майбутніх злетів математики в царині духу: «Способи, за допомогою яких можна дійти до розуміння сутності усіх потаємних речей, усіх таємниць, що містяться в речах». А остання — ніби застерігає від нехтування земними проблемами: «Лови гадів, мишей, виполюй бур'яни, дбай про пишну пряжу, проси в бога Ра тепла, вітру і високої води». Так споконвіку поєднуються в математиці ці дві сили — вільна розумова фантазія і зв'язок з життям у природному та суспільному середовищах.
Архімед З усіх великих античних учених, які займалися математичними дослідженнями, Архімед залишився чи не найпривабливішим для нащадків. Вирішальним чином цьому посприяла винятково плідна його діяльність не тільки як дослідника-теоретика, але і як інженера-практика. Відомо, що Архімед керував усією інженерною службою у сіракузького царя Гієрона, в тому числі — і під час історичної оборони Сіракуз від римлян під час 2-ї Пунічної війни (Сіракузи — рідне місто Архімеда на о. Сицилія). І хоча Плутарх стверджує, що своїм механічним винаходам Архімед не надавав особливого значення, розглядаючи їх лише як «забави геометрії», проте і сучасників, і нащадків вражали в першу чергу ці його «забави».
Плутарх розповідає, що воїни римського консула Марцелла були надовго затримані біля стін Сіракуз небаченими досі машинами. В бійницях були виставлені катапульти, які скидали град ядер і каміння, берегові крани, повертаючись, зачіплювали кораблі за щогли, підіймали і скидали їх у воду, а великі ввігнуті дзеркала палили ворога вогнем. Усе це наводило на нападників невимовний жах. «Як тільки вони помічали, — пише Плутарх, — що із-за фортечного муру показується якийсь канат або колода, то з криком починали тікати, жахаючись, що ось Архімед знову придумав якусь нову машину їм на погибель». В іншій історії повідомляється, що Архімед збудував таку систему блоків і важелів, що з допомогою неї одна людина могла спустити на воду новозбудований величезний корабель «Сіракосія», який призначався для перевезення зерна. Крилатою стала фраза, вимовлена нібито при цьому Архімедом: «Дайте мені точку опори — і я переверну Землю». Для відкачування води в разі необхідності на «Сіракосії» було встановлено ще один видатний винахід Архімеда — так званий архімедів гвинт. Надзвичайно популярною є й історія про золоту царську корону, чистоту золота в якій Архімед перевірив на основі відкритого ним закону про виштовхувальну силу. Архімед загинув на 75-му році життя від руки римського воїна. Сивий старець сидів, розглядаючи накреслені перед собою на піску фігури. «Не чіпай моїх креслень», — були його останні слова. Власне математичними дослідженнями Архімед почав займатися уже в зрілому віці — після 40 років. Але це не завадило йому перевершити усіх математиків, які жили як до нього, так і впродовж багатьох наступних століть — аж до Ньютона і Лейбніца в XVII ст. Основний напрям математичних досліджень Архімеда — вимірювання довжин, площ та об'ємів геометричних фігур. Створені ним для цього методи по суті були методами диференціального та інтегрального числення, відкритими аж через 2 тисячі років після Архімеда. Визначним відкриттям Архімеда стали і його напівправильні многогранники, названі пізніше Архімедовими тілами.
Піфагор і піфагорійці Усім добре відома теорема Піфагора про співвідношення між сторонами прямокутного трикутника. На жаль, цим фактом здебільшого й обмежуються наші знання про внесок Піфагора в науку. Але Піфагор мав також інші, не менш вагомі, наукові здобутки. В першу чергу — це ідея математичного моделювання в природознавстві, а також ідея виділення першооснов (пізніше їх назвуть аксіомами) для логічної розбудови наукових теорій. Піфагор народився на грецькому острові Самос, неподалік від Мілета — батьківщини Фалеса. Кажуть, що саме старий Фалес порадив юному Піфагору за власним прикладом вирушити на навчання у східні країни. Нібито аж 20 років Піфагор навчався мудрості в єгипетських жерців, а ще 12 років — у халдейських магів. Можливо, побував він і в Індії, бо дуже багато ідей з його філософського вчення нагадує вірування індусів. Повернувшись на батьківщину, Піфагор не залишився на Самосі, а втік від тамтешнього правителя до вільної грецької колонії Кротон, розташованої на півдні Італії. Тут він заснував знамените науково-філософське і політичне братство. Одна з легенд стверджує, що саме тоді, тобто уже в зрілому віці, Піфагор одержав і своє ім'я — за те, що володів істиною, наче знаменитий дельфійський оракул, котрий говорив устами жриці — піфії.
Легенда стверджує, що, проходячи одного разу біля кузні, Піфагор почув навдивовижу мелодійне звучання трьох молотів, якими ковалі, куючи залізо, одночасно вдаряли по ковадлу. Зацікавившись причиною такої гармонійності, Піфагор зважив молоти. Виявилося, що їхня вага пропорційна певним початковим числам натурального ряду. Аналогічні результати дало вимірювання струн, що утворювали гармонічні (консонантні) співзвуччя при одночасному звучанні. Саме це нібито й дало Піфагору підстави вважати, що все в природі підкоряється числовим закономірностям, тобто визначається числами. «Все є число» — крилата фраза, що з'явилася в школі Піфагора. Тому вивчення чисел вважалося ключем до пізнання природи. Громом серед ясного неба стало для піфагорійців відкриття ними несумірності сторони і діагоналі квадрата. Це відкриття означало, що навіть відношення відрізків не завжди можна виразити у вигляді відношення цілих чисел. Віра у всесильність цілих чисел похитнулася. Спочатку навіть було вирішено не розголошувати це відкриття і тримати його в суворій таємниці. Легенда стверджує, що з таким рішенням не погодився якийсь Гіппас, котрий і розголосив таємницю. За це його піддали найвищій мірі осуду серед піфагорійців — символічному похованню. Після цього Гіппас нібито й справді потонув під час морської бурі. Як би там не було, але після цього відкриття математичні інтереси піфагорійців перемістилися з арифметики на геометрію. Відтак подальший розвиток грецької математики відбувався під знаком геометрії. Про математичні здобутки самого Піфагора достеменно мало що відомо. За звичаєм, якого дотримувалися в його школі, усі відкриття, здійснені піфагорійцями, приписувалися Учителю, тобто Піфагору. А щоб надійно приховати знання від невтаємничених, їх передавали лише в усній формі. Тому-то й неможливо точно сказати, які з відкриттів, що приписувалися піфагорійцям, належать самому Піфагору, які — його учням чи послідовникам, а які належать іншим ученими. Найвидатнішим математичним відкриттям, яке приписується Піфагору, є, звичайно, знаменита теорема Піфагора. З вавилонських математичних текстів відомо, що у Вавилоні про цю теорему знали принаймні за тисячу років до Піфагора. Тож цілком можливо, що Піфагор дізнався про неї під час своїх подорожей на Схід. Але безсумнівною його (чи його школи) заслугою було логічне доведення цієї теореми. Захоплені цим доведенням, нащадки Піфагора придумали навіть легенду про те, що на знак вдячності богам за це відкриття Піфагор здійснив гекатомбу — тобто приніс у жертву сто биків. Легенда, щоправда, не зовсім узгоджується з морально-етичними переконаннями піфагорійців, які були противниками будь-якої надмірності і не визнавали жертвоприношень живими істотами. Але вона яскраво передає захоплення греків силою розуму.
Як саме доводив Піфагор свою теорему, достеменно не відомо. Тепер відомо сотні різних доведень цієї теореми. Цілком можливо, що саме доведення Піфагора подає Евклід у своїх «Началах» (цікаво, що найважливіша в ідейному плані перша книга цього твору завершується якраз теоремою Піфагора).
Підставою для обрання піфагорійцями символом свого братства саме цієї фігури ймовірно було те, що кожна її сторона ділиться іншими двома сторонами у так званому середньому і крайньому відношенні. Такий поділ здавна називали золотим, він вважався теоретично найдосконалішим і естетично найпривабливішим.
Неважко показати, що діагоналі правильного п'ятикутника (тобто сторони правильного зірчастого
За доби Середньовіччя правильний зірчастий п'ятикутник назвали пентаграмою («пента» означає «п'ять»). Пентаграмі приписувалася здатність захищати від злих духів. Згадаймо, що саме цей знак був накреслений перед порогом доктора Фауста — Мефістофелеві довелося неабияк постаратися, щоб пролізти у щілину між пентаграмою і одвірком. Кажуть, що піфагорійці вже знали про існування правильних многогранників і вміли будувати принаймні три з них — куб, тетраедр і додекаедр. А це свідчить про досить високий рівень їхніх здобутків і в стереометрії. Наступна епоха Платона-Арістотеля-Евкліда мала що перейняти від піфагорійців! Символічно, що гранями одного з правильних многогранників — додекаедра, є правильні п'ятикутники. Лише через дві тисячі років після піфагорійців з'ясувалося, що з додекаедра можна отримати три правильні зірчасті многогранники, гранями яких є правильні зірчасті п'ятикутники. Цікаво, що, крім цих трьох, існує ще лише один правильний зірчастий многогранник. Але і його форма тісно пов'язана з піфагорійською пентаграмою. Евклід і його «Начала» Першим підручником з математики, який повністю зберігся до наших днів, були «Начала» Евкліда. Щоправда, сучасні дослідники мають справу не з оригінальним текстом Евкліда, а з перекладами «Начал» на арабську мову. Коли на уламках античної цивілізації арабські халіфи збудували свою державу, вони дуже мудро повелися з культурним надбанням підкорених народів, повністю перейнявши його. Зокрема, були перекладені арабською мовою праці найвидатніших грецьких учених Арістотеля, Архімеда, Аполлонія, Птоломея і, звичайно ж, Евкліда. Здебільшого саме завдяки арабським перекладам ці твори і дійшли до нас. Про самого Евкліда відомо дуже мало. Народився він в Афінах і замолоду навчався у Платона або (це ймовірніше) в Арістотеля. Пізніше перебрався в Олександрію — грецьку колонію на єгипетському узбережжі Середземного моря, засновану Олександром Македонським. Переїхати до Олександрії його спонукав тамтешній цар Птоломей І — засновник великої правлячої династії. Птоломей І увійшов в історію як цар-просвітник. До Олександрії були запрошені учені мужі з усього світу. Тут при храмі Муз — дев'ятьох легендарних супутниць бога Аполлона, які опікувалися науками та мистецтвами, було побудовано великий палац Мусейон, де на повному державному утриманні жили вчені, займаючись науковими дослідженнями, філософією, поезією і мистецтвом. До їхніх послуг була також величезна бібліотека, у якій зберігалося 500 000 сувоїв наукових і мистецьких праць. На початку III ст. до н.е. сюди прибув Евклід. Працюючи в бібліотеці Мусейону, а можливо, й викладаючи геометрію його мешканцям, Евклід і створив свої «Начала». Про відданість Евкліда науці свідчить така легенда. Нібито один з тих, хто щойно почав навчатися в Евкліда геометрії, опанувавши першу теорему, спитав учителя: «А скільки я зможу заробити, вивчивши все це?» Тоді Евклід покликав раба і наказав: «Дай йому три оболи (обол — дрібна монета), бо цей сіромаха хоче заробити гроші своїм навчанням». Антична наука була аристократичною, її завданням був пошук істини заради самої істини. Будь-який практичний зиск вважався недостойним справжнього мудреця. Лише софісти навчали за гроші. Тому ставлення до них було не вельми прихильним. Вищенаведена легенда увійшла до «Каталогу грецьких геометрів», складеного неоплатоніком Проклом Діодохом Візантійським у V ст. н.е., тобто через сім століть після смерті Евкліда. Протягом деякого часу Прокл жив і працював у тій же Олександрії, що й раніше Евклід. На два століття випереджає Прокла інше авторитетне свідчення про Евкліда, залишене олександрійським математиком Паппом. Повір'я, яке передає Папп, змальовує Евкліда як людину винятково чесну, тиху і скромну, повністю вільну від гордощів та егоїзму. І Папп, і Прокл склали свої коментарі до «Начал» Евкліда, запропонувавши удосконалення окремих доведень з метою надання їм більшої обґрунтованості та для легшого засвоєння. Слід зазначити, що спроби укладання підручників для початкового ознайомлення з геометрією робилися і до Евкліда. Про це повідомляється в деяких історичних джерелах. Але твір Евкліда виявився настільки змістовним і досконалим, що після його оприлюднення про інші швидко забули. Тому-то жоден з них і не зберігся. Своїм твором Евклід подав класичний зразок для побудови не тільки математичних, але й інших наукових теорій. За цим зразком спочатку наводиться перелік основних понять і відношень даної теорії, далі формулюються основні властивості цих понять і відношень (аксіоми), потім вводяться нові означення, доводяться нові теореми і т.д. Як виявилося, цією логічною схемою можна послуговуватися і в інших науках. Тепер це називається аксіоматичним методом і є досить поширеним засобом наукового пізнання. Сам Евклід вдався до аксіоматичного підходу в оптиці, написавши про це спеціальний твір. Пізніше Архімед таким способом викладав окремі питання механіки. Класичним втіленням аксіоматичного методу поза математикою стала фундаментальна праця Ньютона «Математичні начала натуральної філософії», в якій, зокрема, виводяться, як теореми, закон всесвітнього тяжіння та закони Кеплера для руху планет навколо Сонця. Як і Евклід, Ньютон також спочатку формулює аксіоми механіки, а потім виводить наслідки з них — теореми. Навіть самою назвою своєї праці, в якій фігурує слово «начала», Ньютон підкреслює свою прихильність до традиції, закладеної Евклідом. У сучасній науці аксіоматичний метод набуває дедалі більшого поширення. І не суттєво, що аксіоми часто називаються інакше — постулатами, принципами, правилами чи законами. Важливо те, що з цих вихідних положень нові твердження виводяться уже суто логічним шляхом. «Начала» Евкліда складаються з 13 розділів. Кожен розділ був написаний на окремому сувої пергаменту і в ті давні часи називався книгою. В друкованому вигляді весь твір займає тепер одну книгу обсягом приблизно 400 сторінок. Перші шість розділів «Начал» були присвячені планіметрії. Наступні чотири — геометричній теорії дійсних чисел та пропорційності. В останніх трьох розділах викладалася стереометрія. Завершувався твір побудовою так званих правильних многогранників, які тоді відігравали ключову роль в філософії природи. Майже 2,5 тисячі років ознайомлення з геометрією відбувалося винятково за «Началами» Евкліда або за спрощеними варіантами цієї праці. Навіть сучасні підручники мають з «Началами» багато спільних рис. Приміром, і досі планіметрія та стереометрія викладаються окремо, причому приблизно в такому ж порядку і обсязі, що й в Евкліда. Через те й увесь курс геометрії, що вивчається в школі, часто називають евклідовою геометрією. Великі пошуки Однак проблема виявилася не такою простою, як здавалося на перший погляд. У різні часи і в різних місцях за неї бралися найвидатніші математики. Але бажаного результату не досягали. У «доведеннях», які час від часу все ж таки пропонувалися, при більш ретельнішому аналізі виявлялася одна і та ж логічна вада: використовувалися твердження, які, хоча й були наочно очевидні, але не зафіксовані як аксіоми. Більше того, самі ці твердження виявлялися так само еквівалентними V постулату, як йому еквівалентна сучасна аксіома про паралельні прямі. Тому в усіх цих «доведеннях» здійснювалося хибне логічне коло, тобто використовувалося якраз те, що і треба було довести. Потрапляли в це хибне коло навіть найвидатніші математики. Наприклад, Лежандр у своєму «доведенні», яке він помістив навіть в одному з численних видань своїх «Початків геометрії», використовував таке, здавалося б очевидне і незаперечне твердження: через точку А, взяту всередині кута О (рис.6), завжди можна провести пряму, яка перетинає обидві його сторони. Пізніше Лежандр помітив цю свою помилку, і в наступному виданні його підручника V постулат Евкліда знову зайняв своє звичне місце серед аксіом. Нарешті, на початку XIX ст. безуспішність численних спроб довести V постулат наштовхнули тоді ще молодого викладача Казанського університету, а пізніше всесвітньо відомого математика Миколу Івановича Лобачевського (1792-1856) на думку, що доведення, про яке мріяло так багато учених, насправді неможливе. Для підтвердження цієї своєї здогадки Лобачевський почав крок за кроком виводити логічні наслідки з посиланням на твердження, яке було запереченням V постулату Евкліда. Якби таким способом вдалося прийти до суперечності, то це означало б, що зроблене припущення хибне, отже, істинний V постулат. А це й було б омріяним доведенням. Проте суперечності не виникало. Одержані наслідки, щоправда, разюче суперечили щоденному фізичному досвіду. Але логічної суперечності між ними не було. З цього Лобачевський зробив сміливий висновок про неможливість логічного доведення V постулату Евкліда, а одержану низку наслідків з його заперечення назвав «уявною» геометрією. Це феноменальне відкриття поклало початок нової ери в математиці — ери математичних теорій, побудованих на різних системах аксіом. «Уявна» геометрія Лобачевського стала першим прикладом аксіоматичної теорії, відмінної від евклідової геометрії. За це відкриття англійський математик Джеймс Сильвестр (1814-897) назвав Лобачевського «Коперником геометрії». Заради справедливості слід відзначити, що до того ж відкриття, що й Лобачевський, незалежно від нього і майже одночасно з ним прийшли ще два учені — німецький математик Карл Фрідріх Ґаусс (1777-1855) та угорський математик Янош Больяі (1802-1860). Однак їхні дослідження з цієї проблеми не були такими масштабними, а виступи в наукових колах із захистом нових поглядів такими сміливими, як Лобачевського.
Кутомірні інструменти Проблема вимірювання кутів вперше постала перед людьми ще в сиву давнину. Необхідність точного визначення положення Сонця і зірок на небі стимулювала створення спеціальних приладів для визначення кутів, під якими видно ці небесні світила. Одним із перших кутомірних інструментів була астролябія, винайдена Гіппархом (180–125рр. до н.е.), а пізніше удосконалена Регіомотаном (1436–1476). Вона складалася з важкого мідного диска — лімба (рис. 1), який підвішувався за кільце у вертикальному положенні.
Розташувавши площину лімба горизонтально, можна було вимірювати кути і в горизонтальній площині. Для цього після встановлення астролябії алідаду наводили спочатку на один об'єкт спостереження і засікали кут на шкалі лімба, а потім — на другий об'єкт і також засікали кут. Різниця між цими кутами дорівнювала куту відхилення напрямку на один об'єкт відносно напрямку на інший.
Суттєві вдосконалення в конструкції астролябії і квадранта були внесені французьким вченим Жаном Пікаром у середині XVII ст. Пікар замінив діоптри підзорною трубою, винайденою незадовго до нього Галілеєм. Перед лінзою труби він встановив сітку з пересічних волосин, а для плавного руху алідади використовував мікрометричний гвинт, що значно підвищувало точність вимірювань.
Теодоліт має два лімби, розміщені у вертикальній і горизонтальній площинах, що дозволяє вимірювати вертикальні і горизонтальні кути одночасно. На вертикальному лімбі розміщена підзорна труба, з допомогою якої алідада вертикального і горизонтального лімбів наводиться на об'єкт спостереження. Точність вимірювання при цьому складає частки мінути.
Кавальєрі (1598-1647) Бонавентура Кавальєрі народився в Мілані наприкінці XVI ст. в одному з найзнатніших, але збіднілому сімействі. В юнацькі роки він отримав прекрасну гуманітарну освіту. Тому-то навіть у своїх суто математичних працях Кавальєрі часто застосовує найвишуканіші класичні звороти і метафори. Ось як, наприклад, починається передмова до «Геометрії» Кавальєрі: «Подібно до того, як незліченному рою бджіл, що навперебій вражають своїми жалами, не вдається відігнати ведмедя, який впивається медом, якщо він хоч трохи скуштував схованих в дереві солодощів, так само, звичайно, не знайдеш того, хто, хоч краєчком губ попробувавши солодощів математичних доведень (яка б сила щонайбільших труднощів, якими ці доведення супроводжуються, не відштовхувала його, ніби частими уколами жал), не прагнув би всіма силами опанувати їх цілком, до повного насичення. О, друже читачу, що звик куштувати ці медові страви! Я пропоную тобі, палаючому пристрастю до цих солодощів, скуштувати плодів, які виросли в мене під час моїх геометричних досліджень». Ще юнаком Кавальєрі вступив у чернечий орден ієронімітів. Монастир св. Ієроніма знаходився поблизу його дому, і монахи, з якими він постійно зустрічався, справили визначальний вплив на напрямок його освіти. Приблизно у 18-річному віці Кавальєрі перейшов у монастир ієронімітів у Пізі — рідному місті знаменитого Галілея. У Пізі Кавальєрі зблизився з відомим тоді тамтешнім математиком Кастеллі, який, запримітивши в юнакові виняткове математичне обдарування, спочатку сам направляв його розвиток у потрібне русло, а потім познайомив з самим Галілеєм. Той, переконавшись у справедливості захоплених відгуків Кастеллі, спочатку певний час настановляв Кавальєрі, а коли в 1629 р. в Болоньї з'явилася вакансія по кафедрі математики, написав для нього захоплену рекомендацію, в якій молодий математик ставився «в рівень з Архімедом». Разом з рукописом «Геометрії» цієї рекомендації виявилося досить для зайняття вакансії. На цій посаді з великою шаною Кавальєрі перебував до кінця своїх земних днів. Він написав ще декілька об'ємних і змістовних математичних праць. Але жодна з них з погляду майбутнього уже не зрівнялася з «Геометрією неподільних». Пам'ятник Кавальєрі поставлено у Мілані в 1844 р. В лівій руці — сфера, на якій зображено сферичний трикутник АВС і записано відношення З «Думок» Блеза Паскаля Те, що перевершує геометрію, перевершує й нас. Усе повинно бути доведено, і при доведенні не можна використовувати нічого, крім аксіом та раніше доведених теорем. Блез Паскаль Біографи Блеза Паскаля (1623–1662) — різностороннього вченого, філософа, першовідкривача відомого фізичного закону про тиск рідин і газів — розповідають про такий дивовижний факт з його життя. Змалечку, прислухаючись до розмов, що велися в оселі Паскалів під час зібрань провідних тогочасних учених, Блез, звісно, часто чував про геометрію. Тому й запитав у батька одного разу, що то таке. Той, не бажаючи обтяжувати хворобливого і кволого сина ще й математичними заняттями і вбачаючи його майбутнє у вивченні стародавніх мов, неохоче відповів, що геометрія — це, мовляв, така не вельми поважна наука, що вивчає властивості різноманітних паличок, кружечків, коліщаток та інших подібних речей. Проте навіть такого «пояснення» юному Паскалю вистачило для того, щоб самостійно відкрити основи геометрії. Ввівши власну термінологію, креслячи фігури крейдою на підлозі, він самостійно, за допомогою логічних міркувань, дійшов аж до теореми про суму кутів трикутника. Яким же було здивування батька, коли одного разу він застав сина за доведенням непростої геометричної теореми! Батько зрозумів, бо й сам був добрим геометром, що Блез має іскру Божу до математики і вже не лише не перешкоджав, а й всіляко сприяв розвитку синового обдарування. Цей (без сумніву, дещо прикрашений) епізод яскраво ілюструє дедуктивний характер геометрії. З іншого боку, він красномовно вказує й на основне джерело виникнення геометрії — логічний аналіз мисленнєвих образів предметів, що реально існують у навколишньому світі. Додамо у зв'язку з цим, що ретельного логічного аналізу потребували навіть найпростіші геометричні поняття (точки, прямої і площини). Ще Евклід у своїх «Началах» давав їм явні означення. Наприклад, точку він означав як «те, що не має частин», а пряму — як «лінію, що однаково розміщена відносно всіх своїх точок»; саму ж лінію Евклід трактував як «довжину без ширини». Але намагання дати чомусь явне означення є спробою підвести це «щось» під поняття, яке вважається відомим. Наприклад, коли ми означаємо ромб як паралелограм, у якого всі сторони рівні між собою, то вважаємо, що поняття паралелограма нам уже відоме. Зрозуміло, що цей процес не повинен тривати нескінченно. Тому в сучасних викладах геометрії він зупиняється на найпростіших поняттях, означень яких у явному вигляді не приймають (інколи неправильно кажуть, що ці поняття взагалі приймаються без означень), а в неявному вигляді означають за допомогою аксіом. Слід, однак, зауважити, що первісні поняття геометрії є найпростішими тільки з погляду логіки, тобто в тому розумінні, що вони найпростіше означаються — аксіомами, і всі відразу. Натомість із погляду сприйняття, тобто створення в уяві відповідних образів, їх найпростішими не назвеш. Наприклад, уявити обмежений відрізок значно простіше, ніж необмежену пряму. Однак поняття прямої в геометрії є первісним, а поняття відрізка — похідним. Що ж до відбору самих аксіом, то це в історії геометрії було якщо не найважчою, то, безперечно, найдраматичнішою сторінкою — зокрема, вельми складною виявилася доля аксіоми про паралельні прямі, яку протягом двох тисячоліть намагалися довести як теорему. Феофан Прокопович (1681–1736) Протягом тривалого часу «Начала» Евкліда, а також коментарі та додатки до них, складені пізнішими авторами, фактично уособлювали всю математичну науку. Згодом, коли головним предметом інтересу вчених стали етико-філософські і теологічні проблеми, твір Евкліда почали вважати вершиною математичної мудрості, обмежуючись ґрунтовним вивченням лише перших його розділів, у яких викладалися основи планіметрії. Водночас шанобливе ставлення до самої математики в культурному середовищі зберігалося завжди, і математичні знання вважалися необхідним атрибутом справжньої освіченості. Першим навчальним закладом на українських теренах, в якому математиці почали надавати значної ваги, була знаменита Києво-Могилянська академія. А вирішальну роль у цьому відіграв ректор академії, відомий учений, просвітитник, релігійний і культурний діяч Феофан Прокопович. Статус академії Києво-Могилянський колегіум, відкритий ще у 1632р., здобув, за царським указом, у 1701 році. Упродовж усієї історії свого існування цей навчальний заклад був авторитетним освітнім і культурним центром не лише в Україні, але й в цілій Східній Європі. Випускники академії пропагували передові суспільно-політичні та культурологічні ідеї, займали високе становище як у релігійному, так і в світському житті суспільства. Феофан Прокопович народився у Києві, як пише біограф, «у статечних батьків». У 17 років він успішно закінчив Києво-Могилянський колегіум. Бажаючи продовжувати навчання і далі, прийняв унію. Після закінчення Володимир-Волинської єзуїтської колегії, як кращий її випускник, був направлений до римської колегії св. Афанасія. Здібний юнак і там відзначився своїми успіхами: зокрема, здобув право працювати у Ватиканській бібліотеці. Близько 1704 р. Прокопович повернувся до Києва і в 1705 р. став викладачем Академії, а через 7 років його було призначено ректором.
|
|||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 500; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.31.159 (0.068 с.) |
 Це доведення Евкліда базується на такому факті: площі прямокутника і трикутника, що мають спільну основу і рівні висоти (рис. 1), відносяться, як 2:1 (переконайтеся в цьому). Сама ж теорема формулюється так: «У прямокутному трикутнику квадрат, побудований на гіпотенузі, рівновеликий двом квадратам, побудованим на катетах».
Це доведення Евкліда базується на такому факті: площі прямокутника і трикутника, що мають спільну основу і рівні висоти (рис. 1), відносяться, як 2:1 (переконайтеся в цьому). Сама ж теорема формулюється так: «У прямокутному трикутнику квадрат, побудований на гіпотенузі, рівновеликий двом квадратам, побудованим на катетах». Доведення (Евкліда). Нехай АВС — заданий прямокутний трикутник з прямим кутом С, а АСНF, ВСGК, АВЕD — квадрати, побудовані на його сторонах (рис. 2). Проведемо СL ║ АD, а потім відрізки АК, ВF, СD і СЕ. ∆ABF = ∆ADC, а ∆ВАК=∆ВЕС (за першою ознакою). Але площа ∆ABF дорівнює половині площі квадрата АСНF, а площа ∆ADC — половині площі прямокутника АDLМ. Оскільки ж трикутники рівновеликі, то рівновеликі і фігури АСНF та АDLМ. Аналогічно встановлюється, що рівновеликі фігури ВСGК та МВЕL. Цим доведенням теорема Піфагора завершується.
Доведення (Евкліда). Нехай АВС — заданий прямокутний трикутник з прямим кутом С, а АСНF, ВСGК, АВЕD — квадрати, побудовані на його сторонах (рис. 2). Проведемо СL ║ АD, а потім відрізки АК, ВF, СD і СЕ. ∆ABF = ∆ADC, а ∆ВАК=∆ВЕС (за першою ознакою). Але площа ∆ABF дорівнює половині площі квадрата АСНF, а площа ∆ADC — половині площі прямокутника АDLМ. Оскільки ж трикутники рівновеликі, то рівновеликі і фігури АСНF та АDLМ. Аналогічно встановлюється, що рівновеликі фігури ВСGК та МВЕL. Цим доведенням теорема Піфагора завершується. Символом піфагорійського братства був правильний зірчастий п'ятикутник (рис. 3). Піфагорійці носили його на грудях і таким чином могли відразу розпізнати один одного. В одній з легенд стверджується, що подорожній піфагорієць, який не мав чим розплатитися з господарем за нічліг, намалював на стіні його будинку цей знак. Згодом інший піфагорієць, який випадково побачив знайомий символ, щедро заплатив господареві за свого товариша.
Символом піфагорійського братства був правильний зірчастий п'ятикутник (рис. 3). Піфагорійці носили його на грудях і таким чином могли відразу розпізнати один одного. В одній з легенд стверджується, що подорожній піфагорієць, який не мав чим розплатитися з господарем за нічліг, намалював на стіні його будинку цей знак. Згодом інший піфагорієць, який випадково побачив знайомий символ, щедро заплатив господареві за свого товариша. Правильний зірчастий п'ятикутник можна утворити з правильного опуклого п'ятикутника, провівши в ньому діагоналі (рис. 4).
Правильний зірчастий п'ятикутник можна утворити з правильного опуклого п'ятикутника, провівши в ньому діагоналі (рис. 4). За означенням, точка М ділить відрізок АС (рис. 5) в середньому і крайньому відношенні (тобто визначає золотий поділ відрізка АС), якщо відношення меншої частини відрізка до більшої дорівнює відношенню більшої частини до всього відрізка:
За означенням, точка М ділить відрізок АС (рис. 5) в середньому і крайньому відношенні (тобто визначає золотий поділ відрізка АС), якщо відношення меншої частини відрізка до більшої дорівнює відношенню більшої частини до всього відрізка:  .
. п'ятикутника) справді поділяють одна одну в середньому і крайньому відношенні. Для цього проведемо у правильному п'ятикутнику АВСDЕ (рис. 6) діагоналі АС, ВЕ та СЕ. Нехай М — точка перетину перших двох з них. Тоді чотирикутник МСDЕ — ромб, а трикутники АМВ та СМЕ подібні між собою. Звідси випливає:
п'ятикутника) справді поділяють одна одну в середньому і крайньому відношенні. Для цього проведемо у правильному п'ятикутнику АВСDЕ (рис. 6) діагоналі АС, ВЕ та СЕ. Нехай М — точка перетину перших двох з них. Тоді чотирикутник МСDЕ — ромб, а трикутники АМВ та СМЕ подібні між собою. Звідси випливає:  , що й треба було довести.
, що й треба було довести. Лінія
Лінія  займала горизонтальне положення. По краю лімба наносилася шкала, розділена на градуси. До лімба кріпилася стрілка
займала горизонтальне положення. По краю лімба наносилася шкала, розділена на градуси. До лімба кріпилася стрілка 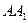 , що називалась алідада, яка могла обертатися відносно центра лімба і мала на кінцях поперечні пластинки з отворами — діоптри. Для визначення висоти зірки над горизонтом спостерігач прикладав око до нижнього діоптра і повертав алідаду так, щоб зірку було видно і через другий діоптр. Поділка на шкалі, на якій зупинявся край алідади, і вказувала висоту зірки в градусах над горизонтом, відзначаючи фактично градусну величину дуги
, що називалась алідада, яка могла обертатися відносно центра лімба і мала на кінцях поперечні пластинки з отворами — діоптри. Для визначення висоти зірки над горизонтом спостерігач прикладав око до нижнього діоптра і повертав алідаду так, щоб зірку було видно і через другий діоптр. Поділка на шкалі, на якій зупинявся край алідади, і вказувала висоту зірки в градусах над горизонтом, відзначаючи фактично градусну величину дуги  .
. Іншим інструментом для вимірювання кутів був квадрант, що являє собою 1/4 частину астролябії. Він мав ту перевагу перед астролябією, що його можна було зробити значно більших розмірів і тим самим збільшити точність вимірювання кутів. На рис. 2 зображено один із квадрантів, сконструйованих видатним данським астрономом Тіхо Браге (1546 – 1601).
Іншим інструментом для вимірювання кутів був квадрант, що являє собою 1/4 частину астролябії. Він мав ту перевагу перед астролябією, що його можна було зробити значно більших розмірів і тим самим збільшити точність вимірювання кутів. На рис. 2 зображено один із квадрантів, сконструйованих видатним данським астрономом Тіхо Браге (1546 – 1601). Найдосконалішим кутомірним інструментом, що застосовується і в наш час при виконанні геодезичних робіт, є теодоліт (рис. 3).
Найдосконалішим кутомірним інструментом, що застосовується і в наш час при виконанні геодезичних робіт, є теодоліт (рис. 3). Одним із найважливіших застосувань вимірювання кутів є знаходження відстаней до недоступних предметів. Нехай потрібно виміряти відстань від пункту А на березі до корабля К, щознаходиться в морі (рис. 4). На березі вибирається ще один пункт В. Вимірюється відстань АВ та кути А і В у трикутнику АВК. Після цього за теоремою синусів легко знайти відстань АК.
Одним із найважливіших застосувань вимірювання кутів є знаходження відстаней до недоступних предметів. Нехай потрібно виміряти відстань від пункту А на березі до корабля К, щознаходиться в морі (рис. 4). На березі вибирається ще один пункт В. Вимірюється відстань АВ та кути А і В у трикутнику АВК. Після цього за теоремою синусів легко знайти відстань АК. , що характеризує площу цього трикутника. Сферична геометрія вважалася основним об'єктом досліджень Кавальєрі.
, що характеризує площу цього трикутника. Сферична геометрія вважалася основним об'єктом досліджень Кавальєрі.


