
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы решения алгебраических иСодержание книги Поиск на нашем сайте
ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ На практике часто приходится решать уравнения вида f (х)=0, где f (x) определена и непрерывна на некотором конечном или бесконечном интервале (a;b). Если функция f (x)представляет собой многочлен, то уравнение называется алгебраическим, если же в функцию f (x)входят элементарные (тригонометрические, логарифмические, показательные и др.) функции, то такие уравнения называются трансцендентными. Всякое значение x*, обращающее функцию в 0, т.е. такое, что f (x*)=0, называется корнем уравнения. Найти корни уравнения точно удается лишь в частных случаях. Кроме того, часто уравнение содержит коэффициенты, известные лишь приблизительно, и, следовательно, сама задача о точном определении корней уравнения теряет смысл. Поэтому разработаны методы численного решения уравнений f (x)=0, которые позволяют отыскать приближенные значения корней этого уравнения. При этом приходится решать 2 задачи: § Отделение корней, т.е. отыскание достаточно малых областей, в каждой из которых находится только один корень уравнения. § Вычисление корней с заданной точностью. При выделении областей, содержащих действительные корни уравнения f (x), можно воспользоваться тем, что если на концах некоторого отрезка непрерывная функция f (x) принимает значения разных знаков, то на этом отрезке уравнение f (x)=0 имеет хотя бы один корень. Отделение корней можно выполнять графически и аналитически. Аналитический способ отделения корней: 1) находим производную f' (x); 2) составляем таблицу знаков функции f (x), полагая x равным: критическим точкам функции или близким к ним; граничным значениям, исходя из области допустимых значений неизвестного; 3) определяем интервалы, на концах которых функция принимает значения противоположных знаков; внутри этих интервалов содержится по одному корню. Графически корни можно отделять двумя способами: 1) строится график функции y = f (x), абсциссы точек пересечения которого с осью Ox являются приближенными корнями уравнения f (x)=0; 2) уравнение y = f (x) записывается в эквивалентном виде j (x)= y (x), так, чтобы графики функций j (x), y (x) строились проще; абсциссы точек пересечения этих графиков тоже являются приближенными корнями уравнения f (x)=0. Метод итераций Уравнение f (x)=0 представляем в виде x = j (x). Выбираем на отрезке [ a,b ] произвольную точку x 0 в качестве начального приближения и строим последовательность: x 1= j (x 0), x 2= j (x 1) ,..., xn = j (xn -1). Процесс последовательного вычисления чисел xn (n =1,2,3,...) называется методом итераций. Если на отрезке [ a,b ] выполнено условие |j' (x) |≤q< 1, то процесс итераций сходится, т.е. увеличивая n, можно получить приближение, сколь угодно мало отличающееся от истинного значения корня уравнения. Процесс итераций продолжается до тех пор, пока не будет выполнено условие |xn-xn -1 |£ Геометрическая интерпретация метода итераций:
Пример: Методом итераций найти корень уравнения f(x)= arcsin(2 x+ 1) -x 2 =0 расположенный на отрезке [-0.5,0] c точностью ε =10-4. Уравнение преобразуем к виду y=j(x) следующим образом: arcsin(2 x +1) =x 2, sin(arcsin(2 x +1)) = sin(x 2), 2 x +1 = sin(x 2), x =0.5(sin(x 2)-1). Значит j (x)= 0.5(sin(x 2)-1), j’ (x)= x cos(x2), | j’ (x) |=|x cos(x 2)|≤0.5 для x Î[ -0.5,0 ]. Метод итераций сходится. Замечание: на каждом этапе необходимо помнить лишь два соседних приближения, поэтому приближение xn обозначим через x, а приближение xn +1через y. Program Iter; {метод итераций} Uses Crt; Const eps=0.0001; Var a,b,x,y,delta:Real; n:Integer; Function Fi(z:Real):Real; Begin Fi:=0.5*(sin(z*z)-1) End; Function Fi1(z:Real):Real; Begin Fi1:=z*cos(z*z) End; Function F(z:Real):Real; Begin F:=2*z+1-sin(z*z); End; Begin Clrscr; Write ('Введите левый конец отрезка а='); ReadLn (а); Write ('Введите правый конец отрезка b='); ReadLn (b); If f(a)*f(b)>0 then Writeln(‘неверен отрезок’) Else Begin X:=(a+b)/2; If abs(Fi1(x))>=1 Then Writeln(‘Метод итераций расходится’) Else Begin n:=0; Repeat y:=Fi(x); delta:=abs(y-x); n:=n+1; x:=y; Until delta<eps; WriteLn('Корень уравнения x=',x:8:4); WriteLn('Проверка f(',x:8:4,')=',f(x):8:5); WriteLn('Количество итераций n=',n); End; End; Repeat Until KeyPressed; End.
Метод половинного деления Для нахождения корня уравнения f (x)=0, принадлежащего отрезку [ a,b ], делим отрезок пополам, т.е. выбираем начальное приближение равным Процесс деления отрезков пополам продолжаем до тех пор, пока длина отрезка, на концах которого функция имеет противоположные знаки, не будет меньше заданной точности e. Пример: Методом половинного деления найти корень уравнения Program Poldel; {метод половинного деления} Uses Crt; Const eps=0.0001; Var x,a,b:Real; Function F(z:Real):Real; Begin F:=z-sqrt(9+z)+z*z-4; End; Begin Clrscr; Write ('Ведите отрезок a,b -->'); ReadLn (a,b); If f(a)*f(b)>0 then Writeln(‘неверен отрезок’) Else Begin Repeat x:=0.5*(b+a); If f(x)=0 then Break; If f(a)*f(x)<0 then b:=x else a:=x; Until b-a<eps; WriteLn ('Корень уравнения x=',x:8:4); WriteLn ('Проверка f(',x:8:4,')=',f(x):8:5); End; Repeat Until KeyPressed; End. Метод Ньютона (касательных) Пусть уравнение f (x)=0 имеет один корень на отрезке [ a, b ], причем f' (x) и f'' (x) определены, непрерывны и сохраняют постоянные знаки на отрезке [ a, b ]. Рассмотрим геометрическую интерпретацию этого метода. Возьмем некоторую точку x 0 отрезка [ a, b ] и проведем в точке P 0{ x 0, f (x 0)} графика функции касательную к кривой y = f (x) до пересечения с осью Ox. Абсциссу x 1 точки пересечения можно взять в качестве приближенного значения корня. Проведя касательную через новую точку P 1{ x 1, f (x 1)} и находя точку ее пересечения с осью Ox, получим второе приближение корня x 2. Аналогично определяются последующие приближения. Выведем формулу для последовательных приближений к корню. Уравнение касательной, проходящей через точку P 0имеет вид:
Полагая y =0, находим абсциссу x 1точки пересечения касательной с осью Ох:
Следующие приближения находим по формулам: Процесс вычислений прекращается при выполнении условия Для сходимости метода начальное приближение x 0 выбирают так, чтобы выполнялось условие f (x 0) f'' (x 0)>0. В противном случае сходимость метода не гарантируется. Пример: Методом Ньютона найти корень уравнения sin(x) -x +0.15=0на отрезке [0.5,1] c точностью ε =0.0001. Найдем f' (x)=cos(x)–1, f'' (x)=–sin(x). Расчетная формула имеет вид:
В качестве начального приближения возьмем x 0=1, т.к. f (1) f'' (1)>0. Вычислим m 1 и M2: m 1 =| cos(0.5)-1 | =0.12, M 2= |- sin(1)|=0.84, значит
Замечание: На каждом этапе необходимо помнить лишь два соседних приближения, поэтому приближение xn обозначим через x, а приближение xn +1через y. Program Kasat; {метод касательных } Uses Crt; Const eps=0.0001; Var a,b,x,y,delta:Real; n:Integer; Function F(z:Real):Real; Begin F:=sin(z)-z+0.15; End; Function F1(z:Real):Real; Begin F1:=(cos(z)-1.0); End; Function F2(z:Real):Real; Begin F2:=-sin(z); End;
Begin Clrscr; Write ('Введите отрезок [a;b]'); ReadLn (a,b); If f(a)*f(b)>0 then Writeln(‘неверен отрезок’) Else Begin x:=a; if F(x)*F2(x)<0 then x:=b; n:=0; Repeat y:=x-F(x)/F1(x); delta:=abs(y-x); n:=n+1; x:=y; Until delta<eps; WriteLn ('Корень уравнения x=',x:8:4); WriteLn ('Проверка f(',x:8:4,')=',F(x):8:5); WriteLn ('Количество приближений n=',n); End; Repeat Until KeyPressed;; End.
Метод хорд Пусть корень уравнения f (x)=0 лежит на отрезке [ a, b ]. Для определенности положим f (a)<0, f (b)>0. Разделим отрезок [ a, b ] в отношении –f (a) :f (b). Это дает приближенное значение корня Далее применим этот прием к тому из отрезков [ a, x 1] и [ x 1, b ] на концах которого функция f (x) имеет противоположные знаки, получим второе приближение корня x 2 и т.д. Геометрически способ пропорциональных частей эквивалентен замене кривой y = f (x) хордой, проходящей через точки N { a, f (a)} и M { b, f (b)}. Если конец b отрезка [ a, b ] неподвижен, то x 0= a и
если конец а отрезка [ a, b ] неподвижен, то x 0= b и
Процесс нахождения последовательных приближений продолжается до тех пор, пока не выполнится условие |xn–xn -1 |£e. Для сходимости метода в качестве начального приближения нужно выбирать тот из концов отрезка, для которого выполняется условие f (x) f'' (x)<0. Неподвижен тот конец отрезка, для которого f (x) f'' (x)>0. Геометрическая интерпретация метода хорд
Определим неподвижный конец f' (x)=3 x 2–0.4 x– 0.2, f'' (x)=6 x –0.4, f (2) f'' (2)>0значит неподвижной будет точка x =2, в качестве начального приближения возьмем x =1. Замечание: На каждом этапе необходимо помнить лишь два соседних приближения, поэтому приближение xn обозначим через x, а приближение xn +1через y. Program Xord; {метод хорд} Const eps=0.001; Var a,b,x,y,delta:Real; n:Integer; Function F(z:Real):Real; Begin F:=z*z*z+0.2*z*z-0.2*z-1.2; End; Function F1(z:Real):Real; Begin F:=3*z*z+0.4*z-0.2; End; Function F2(z:Real):Real; Begin F:=6*z+0.4; End; Begin Write ('Введите отрезок [a;b]'); ReadLn (a,b); If f(a)*f(b)>0 then Writeln(‘неверен отрезок’) Else Begin x:=a; if F(x)*F2(x)>0 then begin x:=b; b:=a; end; n:=0; Repeat y:=x-F(x)/(F(b)-F(x))*(b-x); delta:=abs(y-x); n:=n+1; x:=y; Until delta<eps; WriteLn ('Корень уравнения x=',x:8:4); WriteLn ('Проверка f(',x:8:4,')=',F(x):8:5); WriteLn ('Количество приближений n=',n); End; End.
Комбинированный метод Пусть f (a) f (b)<0и f' (x) и f'' (x) сохраняют постоянные знаки на [ a, b ]. Соединяя метод хорд и касательных, получаем метод, на каждом этапе которого находится значение по недостатку и по избытку точного корня уравнения f (x)=0. Процесс вычисления прекращаем, когда длина отрезка, на котором находится корень уравнения, будет меньше заданной точности ε. За значение корня лучше принять среднее арифметическое полученных последних значений. Геометрическая интерпретация комбинированного метода:
Определим, какой из концов отрезка выбрать в качестве начального приближения по методу хорд, и по методу касательных. Для этого вычислим f' (x)=5 x 4–1, f'' (x)=20 x 3, f (1) f'' (1)<0, значит положим x 1=1 – начальное приближение по методу хорд, x 2=1.1 – начальное приближение для метода касательных. Program Komb; {комбинированный метод} Const eps=0.0005; Var a,b,x,x1,x2,y1,y2,delta:Real; n:Integer; Function F(z:Real):Real; Begin F:=sqr(z)*sqr(z)*z-z-0.2; End; Function F1(z:Real):Real; Begin F1:=5*sqr(z)*sqr(z)-1; End; Function F2(z:Real):Real; Begin F2:=20*sqr(z)*z; End; Begin Write ('Введите отрезок [a,b]-->'); ReadLn (a,b); If F(a)*F2(a)<0 then begin x1:=a; x2:=b; End else begin x1:=b; x2:=a; end; n:=0; Repeat y1:=x1-F(x1)/(F(x2)-F(x1))*(x2-x1); y2:=x2-F(x2)/F1(x2); delta:=abs(y2-y1); n:=n+1; x1:=y1; x2:=y2; Until delta<eps; x:=(x1+x2)/2.0; WriteLn('Корень уравнения x=',x:8:4); WriteLn('Проверка f(',x:8:4,')=',F(x):8:5); WriteLn ('Количество приближений n=',n); End. ПРИБЛИЖЕННЫЕ ВЫЧИСЛЕНИЯ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
Для вычисления определенного интеграла
где xk и Ak определяются квадратурной формулой, R – остаточный член или погрешность квадратурной формулы. Отрезок интегрирования [ a, b ] разбивается на n равных частей системой равноотстоящих точек xi = x 0+ ih, где i= 0,1,2,..., n; x 0= a, xn = b, Квадратурные формулы для равноотстоящих узлов: 1) формула левых прямоугольников:
2) формула правых прямоугольников:
3) формула центральных прямоугольников:
4) формула трапеций:
5) формула Симпсона (формула парабол):
где yi=f(xi), xi=a+ih, 6) формула Ньютона (правило
где yi=f(xi), xi=a+ih, Интегралы считаются с помощью квадратурных формул с точностью e. Для того, чтобы достичь требуемой точности вычисления e, используется способ двойного пересчета: интеграл вычисляют по выбранной квадратурной формуле дважды, сначала с некоторым шагом h, затем с шагом Обозначим результаты разбиений через Jn и J2n соответственно и сравним их. Если |Jn-J2n|<e, где e – погрешность вычислений, то в качестве результата берут J2n. Если |Jn-J2n|³e, то вычисления повторяют с шагом Пример: С помощью формулы трапеций вычислить интеграл
Program Integ1; {Вычисление интеграла по формуле трапеций } {без передачи имени функции в качестве параметра } Uses Crt; Const eps=0.01; Var a,b,eps,integral:Real; nn:Integer; {подинтегральная функция} Function F(z:Real):Real; Begin f:=1/(z-1); End; {процедура вычисления интеграла} Procedure Trap(a1,b1:Real; n:Integer; eps1:Real; var tk:Real); Var i:Integer; x,t0,s,h:Real; Begin t0:=(f(a1)+f(b1))/2*(b-a); {t0–предыдущее значение интеграла} {tk – последующее значение интеграла} While True do Begin h:=(b1-a1)/n; {шаг} s:=(f(a1)+f(b1))/2; For i:=1 to n-1 do Begin x:=a1+i*h; s:=s+f(x); end; tk:=s*h; If abs(tk-t0)<eps1 then Exit; t0:=tk; n:=2*n; {удваиваем количество разбиений} end; End; Begin Clrscr; Write('Введите пределы интегрирования a,b’); ReadLn (a,b); nn:=6; {начальное значение количества разбиений} Trap(a,b,nn,eps,integral); WriteLn('Значение интеграла ',integral:8:4); Repeat Until KeyPressed; End.
{Вычисление интеграла по формуле трапеций } {c передачей имени функции в качестве параметра } Program Integ2; Uses Crt; Const eps=0.01; Type Func= Function (z:Real):Real; Var a,b,eps,integral:Real; nn:Integer; {подинтегральная функция} Function F1(z:Real):Real; Far; Begin F1:=1/(z-1); end; {процедура вычисления интеграла} Procedure Trap(a1,b1:Real; n:Integer; eps1:Real;f:Func; var tk:Real); Var I:Integer; x,t0,s,h:Real; Begin t0:=f(a1)+f(b1)/2; {t0 – предыдущее значение интеграла } {tk – последующее значение интеграла} While True do Begin h:=(b1-a1)/n; {шаг} s:=f(a1)+f(b1)/2; For i:=1 to n-1 do Begin x:=a1+i*h; s:=s+f(x); end; tk:=s*h; If abs(tk-t0)<eps then Exit; t0:=tk; n:=2*n; {удваиваем количество разбиений} end; End; Begin Clrscr; Write('Введите пределы интегрирования a,b'); ReadLn (a,b); nn:=6; {начальное значение количества разбиений} Trap(a,b,nn,eps,F1,integral); WriteLn('Значение интеграла ',integral:8:4); Repeat Until KeyPressed; End.
ЛИТЕРАТУРА 1. Бородич Ю.С. и др. Паскаль для персональных компьютеров: Справ. Пособие / Ю.С.Бородич, А.Н.Вальвачев, А.И.Кузьмич. – Мн.: Выш. шк.: БФ ГИТМП «НИКА», 1991. – 365 с. 2. Вальвачев А.Н., Крисевич В.С. Программирование на языке Паскаль для персональных ЭВМ ЕС: Справ. пособие. – Мн.: Выш.шк., 1989. – 223 с.: ил. 3. Офицеров Д.В. и др. Программирование на персональных ЭВМ: Практикум: Учеб. Пособие / Д.В.Офицеров, А.Б. Долгий, В.А.Старых; Под общ. ред. Д.В.Офицерова. – Мн.: Выш.шк., 1993. – 256 с. 4. Немнюгин С.А. Turbo Pascal: практикум – СПб: Питер, 200. – 256 с.:ил. 5. Пантелеева З.Т. Графика вычислительных процессов: Учеб.пособие. – М.: Финансы и статистика, 1983. – 167 с., ил. 6. Фаронов В.В. Турбо Паскаль 7.0. Начальный курс. Учебное пособие. – М.: «Нолидж», 1997. – 616 с., ил. 7. Фигурнов В.Э. IBM PC для пользователя. Изд. 7-е, перераб. и доп. – М.: ИНФРА – М, 1997. – 640 с.: ил.
Учебное издание
Ружицкая Елена Адольфовна Карасёва Галина Леонидовна Орлов Владимир Васильевич Дёмова Тамара Максимовна
|
||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 323; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.177.204 (0.007 с.) |

 e, где e — заданная точность вычислений. Если q≤0.5, то для прекращения процесса итераций можно пользоваться более простым соотношением |xn-xn -1 |£e.
e, где e — заданная точность вычислений. Если q≤0.5, то для прекращения процесса итераций можно пользоваться более простым соотношением |xn-xn -1 |£e.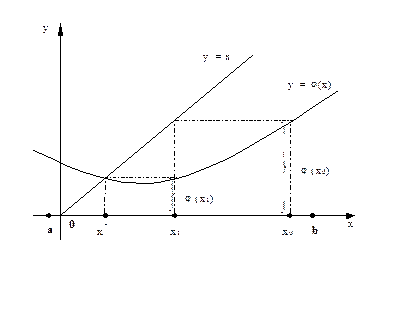
 . Если f (x 0)=0, то x 0 является корнем уравнения. Если f (x 0)¹0, то выбираем тот из отрезков [ a, x 0] или [ x 0, b ], на концах которого функция f (x) имеет противоположные знаки. Полученный отрезок снова делим пополам и проводим те же рассуждения.
. Если f (x 0)=0, то x 0 является корнем уравнения. Если f (x 0)¹0, то выбираем тот из отрезков [ a, x 0] или [ x 0, b ], на концах которого функция f (x) имеет противоположные знаки. Полученный отрезок снова делим пополам и проводим те же рассуждения. на отрезке [2,3]с заданной точностью e =0.0001.
на отрезке [2,3]с заданной точностью e =0.0001.
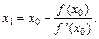

 …,
…,  .
. где
где 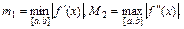 Если
Если  то можно пользоваться более простым соотношением:
то можно пользоваться более простым соотношением: 


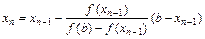 ;
;
 Пример: Методом хорд найти корень уравнения x 3–0.2 x 2–0.2 x– 1.2=0 расположенный на отрезке [1,2]c точностью ε =0.001.
Пример: Методом хорд найти корень уравнения x 3–0.2 x 2–0.2 x– 1.2=0 расположенный на отрезке [1,2]c точностью ε =0.001. Пример: Вычислить с точностью ε =0.0005 комбинированным методом корень уравнения x 5– x– 0.2=0 лежащий на интервале (1,1.1).
Пример: Вычислить с точностью ε =0.0005 комбинированным методом корень уравнения x 5– x– 0.2=0 лежащий на интервале (1,1.1). используют квадратурные формулы вида
используют квадратурные формулы вида
 — шаг разбиения. Затем вычисляем подынтегральную функцию в полученных узлах: yi=f(xi).
— шаг разбиения. Затем вычисляем подынтегральную функцию в полученных узлах: yi=f(xi). где yi=f(xi), xi=a+ih;
где yi=f(xi), xi=a+ih; где yi=f(xi), xi=a+ih;
где yi=f(xi), xi=a+ih;
 где yi=f(xi), xi=a+ih;
где yi=f(xi), xi=a+ih;
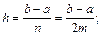
 ):
):
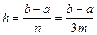 .
. , т.е. удваивают число n (количество точек разбиения [ a, b ]).
, т.е. удваивают число n (количество точек разбиения [ a, b ]). и т.д.
и т.д. с точностью e=0.01.
с точностью e=0.01.


