
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Рівняння першого закону термодинаміки малого елементу процесуСодержание книги
Поиск на нашем сайте
Оскільки T=const, то dT=0, отже, зміни внутрішньої енергії не відбувається, а вся теплота, що підводиться до тіла, переходить в роботу
Оскільки в процесі T=const, то і i=const, тобто не відбувається зміни ентальпії.
Адіабатний процес
Характеристикою адіабатного процесу буде рівність dq=0, тобто теплота до робочого тіла не підводиться і не відводиться. Запишемо рівняння першого закону термодинаміки через ентальпію
Після перетворень одержуємо рівняння
де видно, що
Політропний процес
Розглянемо процес, коли змінюються всі параметри, що беруть участь в процесі. Протягом такого процесу до робочого тіла підводиться (відводиться) теплота q, яка йде частково на зміну внутрішньої енергії робочого тіла, частково на виробництво зовнішньої роботи. Першу частину теплоти, характеризуватимемо коефіцієнтом α, другу – β. Обидва коефіцієнти виразимо в частках від одиниці. Процеси, в яких частка теплоти, що йде на зміну внутрішньої енергії, протягом всього процесу залишається постійною, носять назву політропних. Отже, характеристикою політропного процесу буде постійність величини
або, що те ж саме
Останнє співвідношення витікає з рівняння першого закону термодинаміки. Очевидно, що
Для нескінченно малого політропного процесу коефіцієнт α повинен бути постійним. Тоді
звідси
Рівняння політропного процесу
Для виводу рівняння політропи скористаємося рівнянням першого закону термодинаміки
і
після перетворень
де Одержане рівняння є рівнянням політропи.
Показник політропи можна визначити за рівнянням
Другий закон термодинаміки Якщо перший закон термодинаміки є результатом закону збереження енергії, то другий закон визначає замкнуті термодинамічні процеси або цикли. На діаграмах такі процеси зображаються замкнутими контурами. У використанні до задач термодинаміки другий закон термодинаміки може бути зведений до наступного положення: неможливо здійснити цикл в результаті тільки підвода теплоти до робочого тіла або тільки відведення теплоти від нього. На відміну від «вічного» двигуна першого роду, що створює енергію з нічого, двигун, діючий за наявності одного джерела теплоти, називають «вічним» двигуном другого роду. Тоді другий закон термодинаміки можна сформулювати: вічний двигун другого роду неможливий. Для оцінки економічності прямого циклу використовують відношення роботи за цикл l до теплоти q1, що підводиться. Це відношення називають термічним к. к. д. циклу
Як основна характеристика зворотного процесу приймається величина холодильного коефіцієнта ε, рівного відношенню теплоти, що відводиться від охолоджуваного тіла q2 до роботи l, що витрачається для цього.
Цикл Карно Очевидно, що в даній конкретній термодинамічній системі можна здійснити єдиний оборотний цикл. Цей цикл володітиме максимальною економічністю. Вперше такий цикл і його властивості були розглянуті в роботах С. Карно. Перетворивши рівняння (4.21) можна одержати рівняння для термічного к. к. д. прямого циклу Карно.
Цикл Карно може бути не тільки прямим, але і зворотним. Він є найекономічнішим холодильним циклом. Для зворотного (холодильного) циклу Карно холодильний коефіцієнт буде рівний
Приведена теплота
Відношення кількостей теплоти, що підводиться і відводиться, до відповідної абсолютної температури називається приведеною теплотою. Можна довести, що довільний замкнутий цикл можна замінити нескінченно великою кількістю (n) циклів Карно. В цьому випадку границя суми рівна
який, як відомо з математики, представляється інтегралом, знайденим по замкнутому контуру:
Формула (4.25) справедлива тільки для оборотних циклів. Для необоротного циклу Карно алгебраїчна сума приведених теплот менше нуля.
Аналогічно попередньому для необоротного циклу запишемо
Інтеграл приведених теплот по замкнутому контуру необоротного циклу менше нуля.
Ентропія
Функція S, яка має нескінченно малий приріст dq/T, називається ентропією
Її розмірність для 1 кг робочого тіла буде Дж/(кг К) – питома ентропія. Для m кг робочого тіла ентропія визначається як добуток m·s=S Дж/кг.
|
||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 255; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |


 (4.12)
(4.12)
 . (4.13)
. (4.13) є показником адіабати.
є показником адіабати. (4.14)
(4.14) (4.15)
(4.15) .
. (4.16)
(4.16)
 (4.17)
(4.17) (4.18)
(4.18)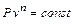 (4.19)
(4.19) – показник політропи.
– показник політропи.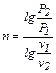 (4.20)
(4.20) (4.21)
(4.21) (4.22)
(4.22) або
або  (4.23)
(4.23)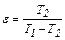 (4.24)
(4.24) ,
, . (4.25)
. (4.25)
 (4.26)
(4.26) (4.27)
(4.27)


