Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Геометрическая сторона задачи.Содержание книги Поиск на нашем сайте Она связана с применением гипотезы Бернулли (плоских сечений) Экспериментально установлено, что при кручении круглого бруса ось стержня не меняет своей длины и формы, а поперечные сечения, плоские и нормальные к плоскости бруса до приложения крутящего момента, остаются такими же после приложения крутящего момента, и поворачиваются друг относительно друга. Физическая модель резинового бруса: поперечные сечения закручиваются друг относительно друга. Выделим участок бруса длиной dz и имеющего радиус r (рис. 8.2).
Рис. 8.2 Участок бруса Пусть левая часть неподвижна.
j - абсолютный угол поворота q - относительный угол закручивания (поворота), приходящийся на единицу длины g - угловая деформация Физическая сторона задачи Заключается в применении закона Гука. Закон Гука для угловых деформаций: t = g×G (5), G – модуль сдвига (модуль упругости II–го рода) Gстали = 8×104 МПа = 8×1010 Па Объединяя три стороны задачи, получаем:
Рис. 8.3 Эпюра касательных напряжений из (4), получаем g = r×q => (5) Mкр =
const Ip Ip = Ix = Iy = p×D4/64; Ip = 2×Ix = 2×Iy = p×D4/32 q = Mкр/ (G×Ip) (7) (7)®(6) => t = (Mкр×r×G)/Ip= (Mкр×r)/Ip t = (Mкр×ri)/Ip (8) Анализируя формулу (8), делаем вывод, что касательные напряжения при кручении распределяются по нормальному закону (рис. 8.3). tmax возникают при r = Wp = Ip/(D/2) – полярный момент сопротивления Для круглого сплошного сечения: Wp = (p×D3)/16 Тогда tmax = Mкр/Wp; Мкр/Wк tmax = Mкр/Wк£ [t] – условие прочности при кручении.
Анализируя эпюру t, мы видим, что в центре сечение не нагружено, т.о. рациональным сечением является не сплошной вал, а кольцо. Задача
 : сопоставить по металлоемкости два равноправных сечения (рис. 8.4). : сопоставить по металлоемкости два равноправных сечения (рис. 8.4).
Рис. 8.4 Полое и сплошное сечения вала Равнопрочные: tmax1 = tmax2 tmax1 = Мкр/Wp1 tmax2 = Мкр/Wp2 Мкр/Wp1 = Мкр/Wp1Þ 1/Wp1 = 1/Wp1 (p×D31)/16 = [(p×D32)/16]×(1–(d24/D24))Þ1/D13 = 1/(D23(1–0.84)); 0.59 D23 = D13; D1 = D×0.839. Сопоставляем сечения 1 и 2 по металлоемкости: F1/F2 = [(p×D12)/4]/[((p×D22)/4)–(1–d22/D22)] = 1.9. 8.2 Кручение прямоугольных стержней При кручении прямоугольных стержней гипотеза плоских сечений не выполняется, так как сечения искривляются - депланируют. Задача о кручении прямоугольных стержней решается в теории упругости. Готовые формулы
Рис. 8.5 Эпюра касательных напряжений для некруглых стержней В углах и центре тяжести 0
где Wk = a×b2×h - момент сопротивления при кручении Ik = b×b3×h - a, b, g -коэффициенты, зависят от соотношения
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 385; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.008 с.) |


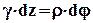
 (4)
(4)
 t×r dF
t×r dF
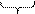 t = r×s× G (6) => (2) Mкр =
t = r×s× G (6) => (2) Mкр =  r2×q×G dF (2) = q×G
r2×q×G dF (2) = q×G 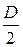
 [t], где Wк – момент сопротивления при кручении, равный в данный момент Wp.
[t], где Wк – момент сопротивления при кручении, равный в данный момент Wp.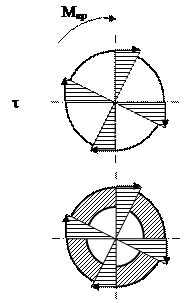 8.1.1 Геометрические характеристики Ip и Wp
8.1.1 Геометрические характеристики Ip и Wp характеристики
характеристики


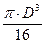











 h>b
h>b