
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статистическая сторона задачиСодержание книги Поиск на нашем сайте
Рис. 6.1 Растяжение стержня
Геометрическая сторона задачи Применим гипотезу плоских сечений: Волокна при растяжении (сжатии) по высоте в поперечном сечении бруса деформируются одинаково Выделим два сечения стержня до приложения нагрузки и рассмотрим их положение в нагруженном состоянии (рис. 6.2).
                    
Рис. 6.2 Деформация стержня Физическая сторона задачи Заключается в применении закона Гука.
Е – модуль упругости 1 рода = 2×105 МПа Объединяем все три стороны задачи
подставляем в интеграл (2)
Найдем растяжение стержня при удлинении, сжатии.
Рис. 6.3 Нормальное напряжение при растяжении
Абсолютная деформация бруса длинной l=e×dz равна
Условия прочности:
Материалы
n – вводится по следующим причинам: · неточное определение внешних нагрузок · приближенные методы расчета · отклонения в размерах деталей · разброс в механических характеристиках материала.
Для хрупких материалов n больше чем для пластичных материалов, так как у хрупких материалов большая неоднородность структуры.
если N(z) = const, F(z) = const
Условие жесткости Dl £ [Dl]
7. Типы задач сопротивления материалов Мы выполняем расчет по допускаемым напряжениям, при этом вся конструкция считается прочной, если напряжение в опасной точке smax не превосходит [s] – допускаемого значения (рис. 7.1).
Рис. 7.1 Эпюра напряжений s Проверочный расчет Дано: Размеры стержня, внешняя нагрузка.
Проектировочный расчет Дано: Внешняя нагрузка, [s]
Определение допустимой внешней нагрузки Дано: размеры стержня, [s] smax =
Расчет на жесткость. Условия жесткости: Dl = Пример (Р-1) все величины заданы в системе СИ
Рис. 39 Пример решения задания Р-1
Рис. 7.2 Пример решения задачи Р-1 Решение Найдем реакции связей
Построим эпюру нормальных сил
Построим эпюру нормальных напряжений
Построим эпюру перемещений
8. Кручение стержней Это такой вид нагружения, при котором в поперечном сечении стержня возникают только крутящие моменты, отличные от 0. а N = Qx = Qy = Mx = My = 0. Стержень, работающий на кручение, называется валом . 8.1 Кручение круглых стержней Три стороны задачи о кручении. Рассмотрим вал, находящийся под действием крутящих моментов (рис. 8.1).
Рис. 8.1 Вал 1. Статическая сторона задачи: Mкр (z) = M, Mкр =
My = N = Анализируя формулы (3), приходим к выводу, что нормальные напряжения в нормальных сечениях s = 0. Найдем закон изменения касательных напряжений “t” в поперечном сечении бруса.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 394; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.01 с.) |





 (1)
(1) (2)
(2)

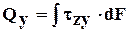



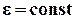 (3).
(3).

 aaïïbb до приложения нагрузки
aaïïbb до приложения нагрузки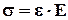 (4) где e - относительная деформация,
(4) где e - относительная деформация,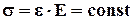 (5)
(5)
 (6) s - нормальное напряжение
(6) s - нормальное напряжение
 E×F – жесткость бруса при растяжении, сжатии.
E×F – жесткость бруса при растяжении, сжатии.
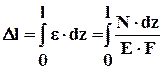 где Dl – абсолютная деформация.
где Dl – абсолютная деформация.
 - допускаемое нормальное напряжение.
- допускаемое нормальное напряжение.
 - предел текучести материала
- предел текучести материала

 - предел прочности материала
- предел прочности материала




 ?
? smax = [s] условие экономичности
smax = [s] условие экономичности
 = [s]
= [s]










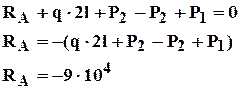




 t×r dF (2)
t×r dF (2) Mx =
Mx =  s ×x×dF = 0 (3)
s ×x×dF = 0 (3)


