
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Построение эпюр нормальных сил NСтр 1 из 5Следующая ⇒
Г.А. Неклюдова
КУРС ЛЕКЦИЙ ПО СОПРОТИВЛЕНИЮ МАТЕРИАЛОВ
Брянск 2007 Оглавление Введение. 3 Объекты исследования сопротивления материалов. 4 1. Метод сечений. 7 Внутренние силовые факторы.. 7 1.1 Построение эпюр внутренних факторов для стержней. 8 1.2 Построение эпюр крутящих моментов. 11 1.3 Построение эпюр поперечных сил Q и изгибающих моментов M для балок. 14 1.3.1 Правило знаков для Q.. 15 1.3.2 Правило знаков для М... 15 2. Дифференциальные зависимости при изгибе. 19 2.1 Правила проверки эпюр. 20 3. Напряжения и деформации. 23 3.1 Интегральные зависимости между s и t и внутренними силовыми факторами. 24 4. Деформации. 25 5. Основные гипотезы, допущения, принципы, принимаемые в курсе сопротивления материалов 27 6. Расчеты на прочность и жесткость при растяжении и сжатии. 29 7. Типы задач сопротивления материалов. 33 8. Кручение стержней. 37 8.1 Кручение круглых стержней. 37 8.1.1 Геометрические характеристики Ip и Wp 40 8.2 Кручение прямоугольных стержней. 41 9. Геометрические характеристики плоских сечений. 45 9.1 Геометрические характеристики простых сечений. 47 9.2 Параллельный перенос осей. 48 9.3 Поворот осей. 49 10. Изгиб. Расчеты на прочность и жесткость при изгибе. 52 10.1 Чистый изгиб. 52 10.2 Поперечный изгиб. 69 11. Определение перемещений в рамах и балках. 75 11.1 Потенциальная энергия деформации системы.. 75 11.2 Обобщенные силы и обобщенные перемещения. 79 11.3 Теорема о взаимности работ и перемещений (теорема Бетти) 81 11.4 Интеграл Мора. 83 11.5 Графо – аналитический метод взятия интегралов (способ Верещагина) 86 11.6 Универсальная формула трапеции. 88 Заключение. 90
Введение Сопротивление материалов- наука, изучающая инженерные методы расчета на прочность жесткость и устойчивость. При эксплуатации конструкции подвергаются действию различных нагрузок. Для нормального функционирования они должны соответствовать необходимым критериям прочности, жесткости и устойчивости. Прочность – свойство конструкции или ее элементов противостоять внешней нагрузке, не разрушаясь. Жесткость – свойство конструкции при нагружении противостоять внешним деформациям. Деформации конструкции при ее нагружении не должны превышать некоторых предварительно заданных весьма малых величин, которые определены из условий нормальной работы конструкции.
Устойчивость – свойство конструкции сохранять первоначальную форму, равновесие при нагружении внешними силами. Расчету на устойчивость подвергаются сжатые стержни. Сопротивление материалов – экспериментально-теоретическая наука, теоретическая часть которой основывается на теоретической механике и математике, а экспериментальная - на физике и материаловедении.
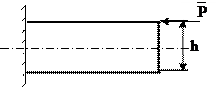
Объекты исследования сопротивления материалов. Стержень – это тело, у которого размеры поперечного сечения b или n значительно меньше его длины l (рис. В1).
Рис. В1 Стержень Оболочка – тело, у которого толщина значительно меньше других размеров (рис. В2).
Рис. В2 Оболочка
Рис. В3 Пластина
Рис. В4 Массивное тело Расчетная схема – схематичное (условное) изображение реального объекта, освобожденного от несущественных с точки зрения данного расчета особенностей. Стержень на расчетной схеме изображается своей осью (рис. В5):
Рис. В5 Расчетная схема двутавровой балки Внешние нагрузки приводятся к оси стержня (см. рис. В6):
Рис. В6 Приведение внешних нагрузок Ось стержня – это геометрическое место центров тяжести поперечных сечений стержня. Силы разделяют на внешние и внутренние. Внешние силы приложены к конструкции, а внутренние возникают в элементах конструкции. Внешние силы подразделяются на поверхностные, приложенные к участкам поверхности, и объемные, распределенные по всему объему конструкции (например, сила тяжести, магнитного притяжения, силы инерции при ускоренном движении конструкции – это объемные внешние силы). Поверхностные силы могут быть сосредоточенными, если они приложены к малым участкам поверхности, или распределенными, если они приложены к конечным участкам.
На расчетной схеме внешние силы приводятся к центру тяжести поперечного сечения стержня (см. рис. В7).
Рис. В7 Приведение внешних нагрузок
1. Метод сечений. Внутренние силовые факторы Внешние силы стремятся разрушить конструкции или узлы, а внутренние силы противодействуют этому.
Рис. 1.1 Приведение внешних нагрузок Чтобы найти внутренние силы воспользуемся методом сечений РОЗУ (рис. 1.2). Р – разрезаем произвольной плоскостью на А и В. О – отбрасываем одну из этих частей, например, В (рис. 1.2а). Рассмотрим оставшуюся часть(рис. 1.2б).
б)
в)
Рис. 1.2 Метод сечений РОЗУ Раскладываем главный вектор и главный момент в плоскости на оси (рис. 1.2в). Внутренние силовые факторы: Qx, Qy – вызывают сдвиг – перерезывающие поперечные силы; N – нормальная продольная шина, растяжение, сжатие бруса; Мz – крутящий момент; Мx, Мy – изгибающий момент (рис. 1.2в). В общем случае нагружения в сечении действуют 6 внутренних факторов. График изменения внутреннего фактора при передвижении вдоль оси стержня называется – эпюрой. У – уравновешиваем. 1.1 Построение эпюр внутренних факторов для стержней Рис. 1.3 Стержень Порядок построения эпюр: 1. Определяем реакции опор. 2. Разбиваем стержень на участки. Участок – часть стержня между точками приложения сосредоточенных сил, включая опорные реакции. 3. Записываем аналитические выражения для внутренних силовых факторов. 4. Строим график (эпюру) (рис. 1.4).
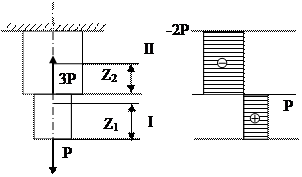
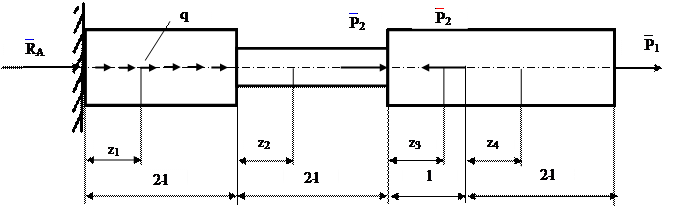
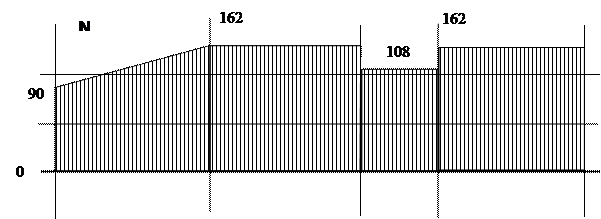
Рис. 1.4 Построение эпюры нормальных сил Эпюра – график, заштрихованный линиями, перпендикулярными оси. Используя метод РОЗУ, отбрасывают ту часть, где больше нагрузки. Внутренний фактор – равнодействующая внутренних сил. Nz2 = P-3P = -2P Nz2 = P-3P = -2P Пример 2 (рис. 1.5). Построить эпюру нормальных сил N. q – интенсивность равномерно – распределенной нагрузки. Опасное сечение в заделке, т.к. там самое большое значение N.
Рис. 1.5 Построение эпюры нормальных сил
Построим эпюру нормальных сил
1.2 Построение эпюр крутящих моментов Под кручением понимается такой вид нагружения, при котором в поперечных сечениях стержня возникает только крутящий момент, а прочие силовые факторы равны нулю. Для крутящего момента, независимо от формы сечения, принято следующее правило знаков.
Рис. 1.6 Правило знаков для крутящего момента Если со стороны внешней нормали к сечению вращение осуществляется против часовой стрелки, то крутящий момент положительный (рис.1.6). Правило знаков носит формальный характер (можно установить произвольно).
Рис.1.7 Схематичное изображение крутящего момента (против часовой стрелки).
Пример(К - 1) Построить эпюру крутящих моментов (рис 1.9).
Рис.1.9 Построение эпюры крутящих моментов
Рис.1.10 Построение эпюры крутящих моментов
1.3 Построение эпюр поперечных сил Q и изгибающих моментов M для балок Балка – стержень, в основном работающий на изгиб. При расчете балку принято заменять ее осью, все нагрузки приводятся к этой оси, а силовая плоскость будет совпадать с плоскостью чертежа. Вал – стержень в основном работающий на кручение. Виды опор:
Рис.1.11 Шарнирно-подвижная опора Шарнирно-неподвижная опора – опора, в которой могут возникать две составляющие реакции: вертикальная и горизонтальная (рис.1.12).
Рис.1.12 Шарнирно-неподвижная опора Заделка (жесткое защемление) – опора, в которой могут быть: вертикальная и горизонтальная реакции и опорный момент (рис.1.13).
Рис.1.13 Заделка
     1.3.1 Правило знаков для Q 1.3.1 Правило знаков для Q
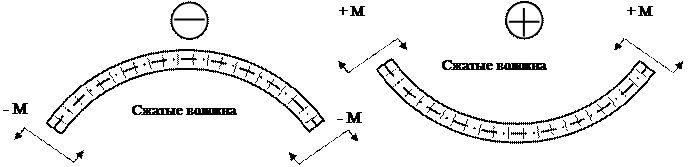
1.3.2 Правило знаков для М Эпюру для М строят на сжатых волокнах.
Пример (Э-3) Построить эпюры внутренних усилий Q и M для однопролетной балки (рис. 1.14).
Рис. 1.14 Расчетная схема Дано: Р=0,5qa M=0,5qa2 Решение: Вычислим реакции опор. Освободим балку от связей и заменим их действие реакциями. Y: RA-P-q·2a+RB=0 Составим уравнения равновесия: Сумма моментов всех сил относительно точки А равна
откуда
Сумма моментов всех сил относительно точки В равна
Разделим балку на четыре участка. Применим метод сечений на каждом из участков и запишем выражения для внутренних усилий
Внутренние усилия на втором участке равны
На третьем участке
Внутренние усилия на четвертом участке равны
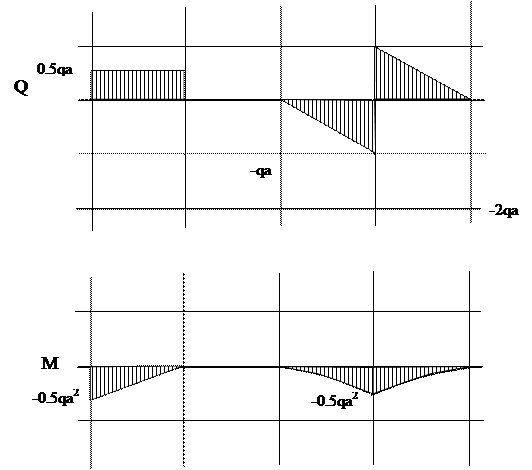
Строим эпюры для M и Q (рис 1.15). Для проверки правильности полученных эпюр могут быть использованы следствия из дифференциальных зависимостей между Q и M.
Рис. 1.15 Построение эпюр Q и M
2. Дифференциальные зависимости при изгибе Пусть стержень закреплен произвольным образом и нагружен распределенной нагрузкой q=f(z), принятое направление q считать положительным (рис. 2.1).
Рис. 2.1 Стержень с распределенной нагрузкой Выделим из стержня элемент длиной dz и в проведенных сечениях приложим моменты M и M+dM, а также поперечные силы Q и Q+dQ (рис. 2.2). В пределах малого отрезка dz нагрузку q можно считать равномерно распределенной.
Рис. 2.2 Элемент длиной dz стержня Приравниваем нулю сумму проекций всех сил на вертикальную ось y и сумму моментов относительно поперечной оси:
После упрощения получим
Из полученных соотношений можно сделать некоторые общие выводы о характере эпюр изгибающих моментов и поперечных сил для прямого стержня. 2.1 Правила проверки эпюр 1. Если на участке отсутствует распределенная нагрузка, то есть q = 0,
Рис. 2.3 Эпюра поперечных сил и изгибающих моментов 2. Если в сечении приложена сосредоточенная сила, то на эпюре Q скачек на величину этой силы, от начала предыдущего, до начала следующего. А на эпюре М излом, направленный навстречу этой силе. 3. Если первая производная положительная, то момент возрастает слева направо, если отрицательная, то наоборот: +Q => M -Q => M¯. 4.
Рис. 2.4 Эпюра поперечных сил и изгибающих моментов 5. Рис. 2.5 Эпюра поперечных сил и изгибающих моментов 6. Если на участке эпюра Q меняет знак и пересекает ось, то эпюра М имеет экстремум в точке пересечения Q с осью. 7. Если ветви эпюры Q сопрягаются без скачка на границах участка, то ветви эпюры М на границе этих же участков сопрягаются без изломов (рис. 2.6).
Рис. 2.6 Эпюра поперечных сил и изгибающих моментов 8. Если на участке стержня Q равна нулю, то
Рис. 2.7 Эпюра поперечных сил и изгибающих моментов 3. Напряжения и деформации
Рис. 3.1 Поперечное сечение бруса Введем понятие касательного и нормального напряжений:
Нормальное напряжение – это предел отношения нормальной составляющей внутренних усилий DN, действующих на элементарную площадку DF при стремлении последней к нулю.
Касательное напряжение – это предел отношения тангенциальной составляющей внутренних усилий DT, действующих на элементарную площадку DF при стремлении последней к нулю.
Общий вид формул:
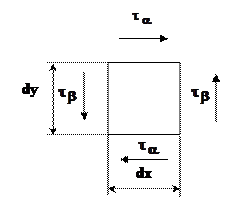
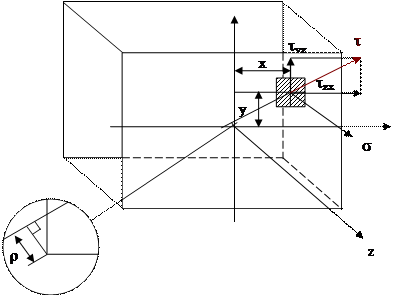
Закон парности касательных напряжений «Вырежем» элементарную площадку dF бруса размером dx на dy (рис. 3.2).
Рис. 3.2 Площадка dF На двух взаимно перпендикулярных площадках, имеющих общее ребро, касательные напряжения 3.1 Интегральные зависимости между s и t и внутренними силовыми факторами
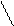  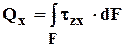
Рис. 3.3Связь между напряжениями и внутренними усилиями
4. Деформации Ни один из существующих в природе материалов не является абсолютно твердым; под действием внешних сил все тела в той или иной мере меняют свою форму(деформируются). Изменение формы напряженного тела существенно влияет на распределение в нем внутренних сил, хотя само по себе это изменение формы является, как правило, незначительным и обнаруживается в большинстве случаев только при помощи чувствительных приборов. Рассмотрим основные виды деформации, которые учитываются при решении задач в сопротивлении материалов. Абсолютная деформация Пусть левый конец стержня зафиксирован, к обоим концам стержня приложена горизонтальная сила P (рис. 4.1). Абсолютная деформация – это полное удлинение стержня, т.е. перемещение свободного конца стержня относительно положения этого конца в ненагруженном состоянии стержня.
Рис. 4.1 Растяжение стержня Относительная деформация
вдоль оси y - ey) Рис. 4.2 Относительная угловая деформация Рис. 5.1 Принцип суперпозиции 7.
   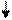  Принцип Сен-Венана. На расстоянии равном размеру поперечного сечения бруса способ приложения нагрузки не оказывает влияния на напряженно деформированное состояние бруса (рис. 5.2). Принцип Сен-Венана. На расстоянии равном размеру поперечного сечения бруса способ приложения нагрузки не оказывает влияния на напряженно деформированное состояние бруса (рис. 5.2).
Рис. 5.2 Принцип Сен-Венана 8. Деформации конструкции малы и не влияют на взаимное положение точек приложения внешних сил и изменение размеров конструкции.
6. Расчеты на прочность и жесткость при растяжении и сжатии Растяжение – такой вид нагружения, при котором в поперечном сечении стержня возникают только нормальные силы N, а все остальные внутренние силовые факторы (поперечные силы, крутящий и изгибающий моменты) равны нулю. Приложение нормальных сил к стержню может быть различным, но в любом случае система внешних сил образует равнодействующую Р, направленную вдоль оси стержня, то есть во всех поперечных сечениях стержня возникают нормальные силы N, равные силе Р: N=P. При расчетах в сопротивлении материалов сжатие отличается от растяжения формально только знаком силы N. Таким образом, при рассмотрении задач сохраняется единство подхода к вопросам растяжения и сжатия. Если для нагруженного по концам растянутого однородного стержня напряжения остаются постоянными как по сечению, так и по длине, то такое напряженное состояние называется однородным. Рассмотрим задачу о распределении напряжений Три стороны задачи о растяжении и сжатии стержня. Рис. 6.1 Растяжение стержня
Рис. 6.2 Деформация стержня Физическая сторона задачи Заключается в применении закона Гука.
Е – модуль упругости 1 рода = 2×105 МПа Объединяем все три стороны задачи
подставляем в интеграл (2)
Найдем растяжение стержня при удлинении, сжатии.
Рис. 6.3 Нормальное напряжение при растяжении
Абсолютная деформация бруса длинной l=e×dz равна
Условия прочности:
Материалы
n – вводится по следующим причинам: · неточное определение внешних нагрузок · приближенные методы расчета · отклонения в размерах деталей · разброс в механических характеристиках материала.
Для хрупких материалов n больше чем для пластичных материалов, так как у хрупких материалов большая неоднородность структуры.
если N(z) = const, F(z) = const
Условие жесткости Dl £ [Dl]
7. Типы задач сопротивления материалов Мы выполняем расчет по допускаемым напряжениям, при этом вся конструкция считается прочной, если напряжение в опасной точке smax не превосходит [s] – допускаемого значения (рис. 7.1).
Рис. 7.1 Эпюра напряжений s Проверочный расчет Дано: Размеры стержня, внешняя нагрузка.
Проектировочный расчет Дано: Внешняя нагрузка, [s]
Расчет на жесткость. Условия жесткости: Dl = Пример (Р-1) все величины заданы в системе СИ
Рис. 39 Пример решения задания Р-1
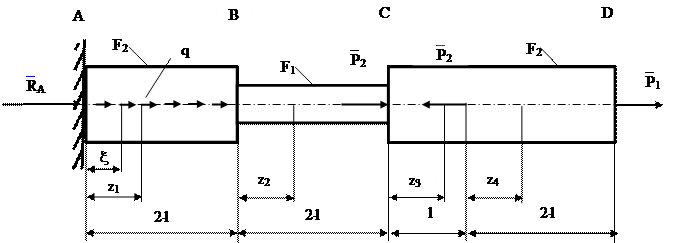
Рис. 7.2 Пример решения задачи Р-1 Решение Найдем реакции связей
Построим эпюру нормальных сил
Построим эпюру нормальных напряжений
Построим эпюру перемещений
8. Кручение стержней Это такой вид нагружения, при котором в поперечном сечении стержня возникают только крутящие моменты, отличные от 0. а N = Qx = Qy = Mx = My = 0. Стержень, работающий на кручение, называется валом . 8.1 Кручение круглых стержней Три стороны задачи о кручении. Рассмотрим вал, находящийся под действием крутящих моментов (рис. 8.1).
Рис. 8.1 Вал 1. Статическая сторона задачи: Mкр (z) = M, Mкр =
My = N = Анализируя формулы (3), приходим к выводу, что нормальные напряжения в нормальных сечениях s = 0. Найдем закон изменения касательных напряжений “t” в поперечном сечении бруса.
Рис. 8.2 Участок бруса Пусть левая часть неподвижна.
j - абсолютный угол поворота q - относительный угол закручивания (поворота), приходящийся на единицу длины g - угловая деформация Физическая сторона задачи Заключается в применении закона Гука. Закон Гука для угловых деформаций: t = g×G (5), G – модуль сдвига (модуль упругости II–го рода) Gстали = 8×104 МПа = 8×1010 Па Объединяя три стороны задачи, получаем:
Рис. 8.3 Эпюра касательных напряжений из (4), получаем g = r×q => (5) Mкр =
const Ip Ip = Ix = Iy = p×D4/64; Ip = 2×Ix = 2×Iy = p×D4/32 q = Mкр/ (G×Ip) (7) (7)®(6) => t = (Mкр×r×G)/Ip= (Mкр×r)/Ip t = (Mкр×ri)/Ip (8) Анализируя формулу (8), делаем вывод, что касательные напряжения при кручении распределяются по нормальному закону (рис. 8.3). tmax возникают при r = Wp = Ip/(D/2) – полярный момент сопротивления Для круглого сплошного сечения: Wp = (p×D3)/16 Тогда tmax = Mкр/Wp; Мкр/Wк tmax = Mкр/Wк£ [t] – условие прочности при кручении.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 999; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.58.169 (0.363 с.) |
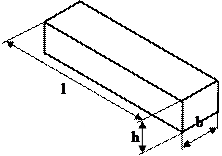
 Серединная поверхность – это геометрическое место точек, равноудаленных от внешней и внутренней поверхностей оболочки.
Серединная поверхность – это геометрическое место точек, равноудаленных от внешней и внутренней поверхностей оболочки. Пластина – оболочка, у которой серединная поверхность – плоскость (рис. В3).
Пластина – оболочка, у которой серединная поверхность – плоскость (рис. В3). Массивное тело – это тело, у которого все три размера сопоставимы (рис. В4).
Массивное тело – это тело, у которого все три размера сопоставимы (рис. В4).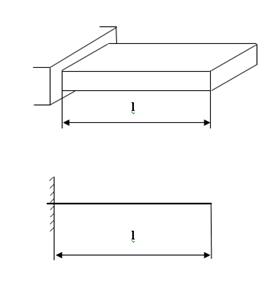

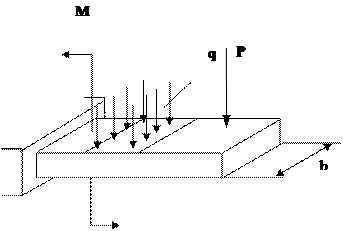
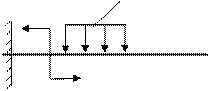
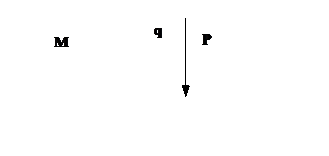
 Рассмотрим произвольный брус, нагруженный самоуравновешенной системой сил (рис. 1.1):
Рассмотрим произвольный брус, нагруженный самоуравновешенной системой сил (рис. 1.1):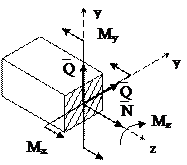 З – заменяем. Внутренние силы мы заменяем главным вектором и главным моментом.
З – заменяем. Внутренние силы мы заменяем главным вектором и главным моментом.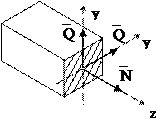 а)
а)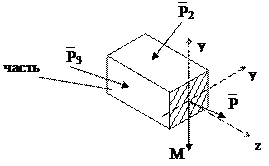

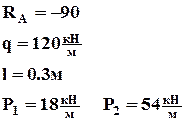
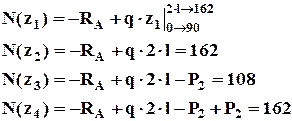

 Стержень, в основном работающий на кручение, называется валом.
Стержень, в основном работающий на кручение, называется валом.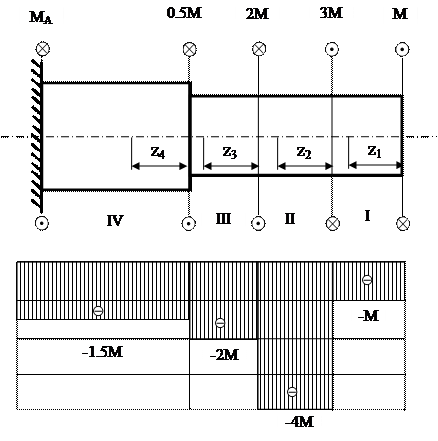

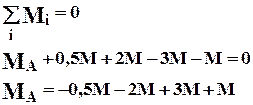

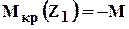
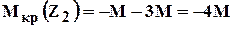
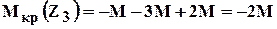
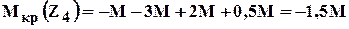
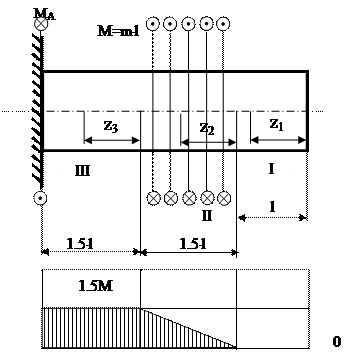 Пример на построение эпюры крутящих моментов (рис 1.10).
Пример на построение эпюры крутящих моментов (рис 1.10).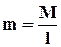
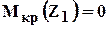
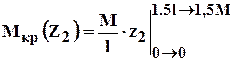
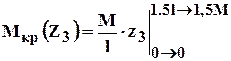
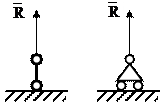 Шарнирно-подвижная опора – опора, в которой может возникать только одна составляющая реакции, направленная вдоль опорного стержня (рис.1.11).
Шарнирно-подвижная опора – опора, в которой может возникать только одна составляющая реакции, направленная вдоль опорного стержня (рис.1.11).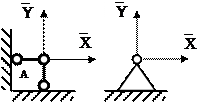

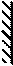


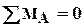
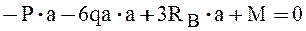
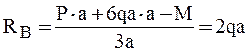
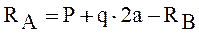
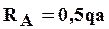
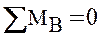
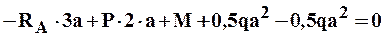
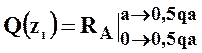
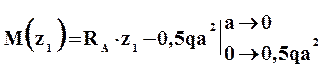
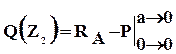
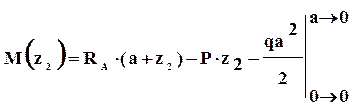
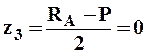
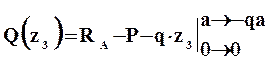
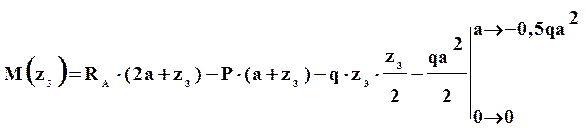
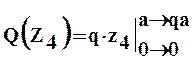
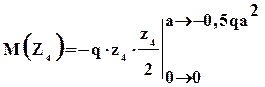
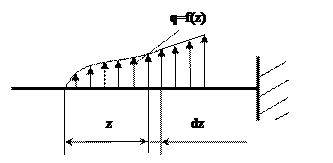

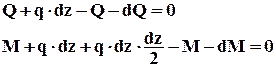
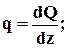
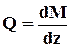
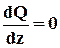 =>Q=const=C1;
=>Q=const=C1; 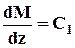 => M=C1×z+D1,то эпюра поперечных сил постоянна, а эпюра изгибающих моментов М изменяется по линейному закону (рис. 2.3).
=> M=C1×z+D1,то эпюра поперечных сил постоянна, а эпюра изгибающих моментов М изменяется по линейному закону (рис. 2.3).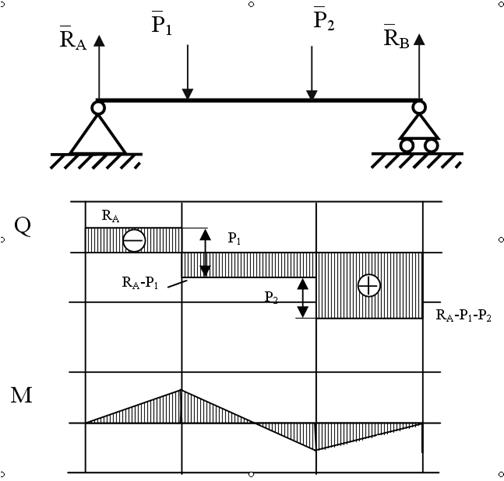
 Если в сечении приложен сосредоточенный момент Мi, то на эпюре Q нет никаких изменений, а на эпюре М скачек на величину этого момента (рис. 2.4).
Если в сечении приложен сосредоточенный момент Мi, то на эпюре Q нет никаких изменений, а на эпюре М скачек на величину этого момента (рис. 2.4).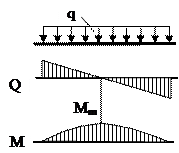 Если на участке приложена равномерно распределенная нагрузка q = const, то Q – наклонная прямая, а М – парабола, выпуклость которой направлена навстречу нагрузке (рис. 2.5).
Если на участке приложена равномерно распределенная нагрузка q = const, то Q – наклонная прямая, а М – парабола, выпуклость которой направлена навстречу нагрузке (рис. 2.5).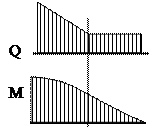
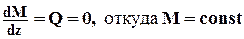 (рис. 2.7)
(рис. 2.7)

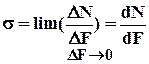 нормальное напряжение
нормальное напряжение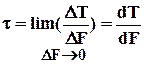 касательное напряжение
касательное напряжение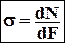
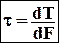
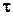
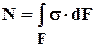
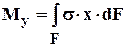
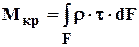
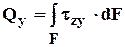




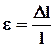 e - относительная деформация (вдоль оси х - ex,
e - относительная деформация (вдоль оси х - ex,
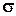 и
и  (1)
(1) (2)
(2)

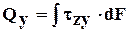



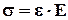 (4) где e - относительная деформация,
(4) где e - относительная деформация,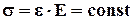 (5)
(5)
 (6) s - нормальное напряжение
(6) s - нормальное напряжение
 E×F – жесткость бруса при растяжении, сжатии.
E×F – жесткость бруса при растяжении, сжатии.
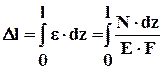 где Dl – абсолютная деформация.
где Dl – абсолютная деформация.
 - допускаемое нормальное напряжение.
- допускаемое нормальное напряжение.
 - предел текучести материала
- предел текучести материала

 - предел прочности материала
- предел прочности материала




 ?
? smax = [s] условие экономичности
smax = [s] условие экономичности






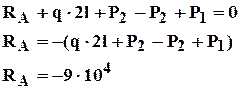




 t×r dF (2)
t×r dF (2) Mx =
Mx =  s ×x×dF = 0 (3)
s ×x×dF = 0 (3)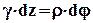
 (4)
(4)
 t×r dF
t×r dF
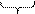 t = r×s× G (6) => (2) Mкр =
t = r×s× G (6) => (2) Mкр = 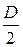
 [t], где Wк – момент сопротивления при кручении, равный в данный момент Wp.
[t], где Wк – момент сопротивления при кручении, равный в данный момент Wp.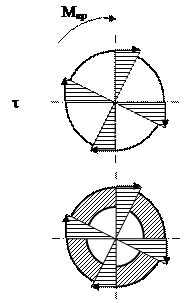 8.1.1 Геометрические характеристики Ip и Wp
8.1.1 Геометрические характеристики Ip и Wp


