
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Загальні властивості функційСодержание книги Поиск на нашем сайте
Означення. Множина всіх значень аргументу, для яких можна обчислити значення функції, називається природною областю визначення функції. Область визначення може бути заданою; у цьому випадку вона залежить також від умови задачі. Приклад. Знайти область визначення функції
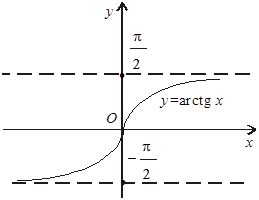
D (y) = (– 1; 0) Означення. Функція y = f (x) називається парною (непарною), якщо для будь-якого х Î D виконується умова f (– x) = f (x) (f (– x) = – f (x)). Функція буде ні парною, ні непарною, якщо для х Î D, f (– x) ¹ ± f (x). Приклад. y = cos x — парна функція (графік функції симетричний відносно осі ординат (рис. 3.2)), бо y (x) = cos(– x) = cos x = = y (x); y = arctg x — непарна функція (графік функції симетричний відносно початку координат (рис. 3.3)), бо y (– x) = ±arctg(– x) = = – arctg x = – y (x); y = arccos x — ні парна, ні непарна (рис. 3.4), бо y (– x) = arccos(– x) = p – arccos x ¹ ± y (x).
Рис. 2.2 Рис. 2.3 Означення. Функція Приклад.
Означення. Функція Приклад. Означення. Функція Приклад.
Рис. 2.6 Рис. 2.7 Елементарні функції Основні з них: 1) степенева 2) показникова 3) логарифмічна 4) тригонометричні: 5) обернені тригонометричні:
Рис. 2.10 Рис. 2.11
Функція вважається елементарною, якщо вона може бути побудована з основних елементарних функцій за допомогою скінченної кількості алгебраїчних дій та суперпозицій, наприклад:
Означення. Функція
де Приклад. Функція
Усі неалгебраїчні функції називаються трансцендентними. Алгебраїчні функції поділяються на раціональні (цілі й дробові) та ірраціональні. Цілою раціональною функцією буде упорядкований многочлен
Дробово-раціональною функцією буде відношення многочленів
Лекція 1 (частина 2) Границя числової послідовності
|
|||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 181; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.136.117 (0.01 с.) |

 .
.
 (0; 1] — природна область визначення. Якщо за умовою задачі х — відстань, а це означає, що х ³ 0, тоді D (y) = (0; 1] — задана область визначення.
(0; 1] — природна область визначення. Якщо за умовою задачі х — відстань, а це означає, що х ³ 0, тоді D (y) = (0; 1] — задана область визначення.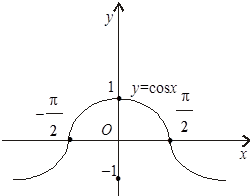
 називається періодичною, якщо для
називається періодичною, якщо для  виконується умова
виконується умова 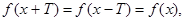 де число Т – період функції.
де число Т – період функції. – періодична функція з мінімальним періодом Т = p (див. рис. 3.5), бо
– періодична функція з мінімальним періодом Т = p (див. рис. 3.5), бо 

 називається обмеженою на множині D, якщо для всіх
називається обмеженою на множині D, якщо для всіх 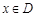 виконується умова
виконується умова  де
де  – деяке скінченне число.
– деяке скінченне число. – обмежена функція для всіх х Î [– 1; 1] (рис. 2.6), бо
– обмежена функція для всіх х Î [– 1; 1] (рис. 2.6), бо  .
. називається монотонно зростаючою (спадною) на множині D, якщо для всіх
називається монотонно зростаючою (спадною) на множині D, якщо для всіх 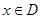 більшому значенню аргументу відповідає більше (менше) значення функції, тобто
більшому значенню аргументу відповідає більше (менше) значення функції, тобто 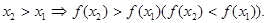
 – монотонно спадна функція при 0 < a <1, а при а > 1 – монотонно зростаюча (рис. 2.7).
– монотонно спадна функція при 0 < a <1, а при а > 1 – монотонно зростаюча (рис. 2.7).


 (рис. 2.8);
(рис. 2.8); (рис. 2.7);
(рис. 2.7); (рис. 2.2);
(рис. 2.2);  (рис. 2.9);
(рис. 2.9);  (рис. 2.5);
(рис. 2.5);  (рис. 2.10);
(рис. 2.10);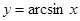 (рис. 2.6);
(рис. 2.6);  (рис. 2.4);
(рис. 2.4);  (рис. 2.5);
(рис. 2.5); 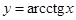 (рис. 2.11).
(рис. 2.11).



 – елементарна функція.
– елементарна функція.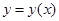 називається алгебраїчною, якщо
називається алгебраїчною, якщо  – розв’язок рівняння
– розв’язок рівняння
 – многочлени.
– многочлени. буде алгебраїчною, бо вона є розв’язком рівняння
буде алгебраїчною, бо вона є розв’язком рівняння .
.
 , або
, або  .
.


