
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Зведення поняття границі функції до границі послідовностіСодержание книги
Поиск на нашем сайте
Послідовність за означенням є функція, отже, границя послідовності – просто окремий випадок границі функції. Навпаки, у деякому розумінні границя функції може бути зведена до границі послідовності. Нехай задано функцію Означення. Число b називається границею функції Відповідно до означення поняття границі функції фактично зведено до поняття границі послідовності, тому теореми про границі послідовностей також справджуються для границь функцій, тобто не потрібно формулювати ці теореми ще раз для границь функцій. 2.2.3. Розкриття невизначених виразів типу При виконанні граничного переходу у виразах типу Розглянемо деякі загальні рекомендації щодо дослідження таких невизначених виразів, обмежуючись тільки алгебраїчними функціями. 1. Невизначеність Спочатку нагадаємо деякі положення алгебри многочленів. Многочлен
Теорема (Безу). Остача від ділення многочлена Наслідок. Якщо число а – корінь многочлена Приклад. Розкласти на множники
Отже,
Розглянемо За наслідком з теореми Безу чисельник і знаменник діляться без остачі на х – а, тобто чисельник і знаменник мають спільний множник х – а. Отже, дістаємо:
Степінь многочленів як у чисельнику, так і в знаменнику зменшився на одиницю. Якщо після виконання нового граничного переходу знову буде невизначеність Зауважимо, що скорочення дробу на множник х – а під знаком границі можливе, бо за означенням границі функції змінна х як завгодно близька до числа а, але
Приклад.
Отже, невизначеність 2. Невизначеність Для розв’язування задач у цьому випадку рекомендується звільнитись від тих ірраціональних множників у чисельнику і знаменнику дробового виразу, які перетворюються на нуль при виконанні граничного переходу. Для звільнення від радикалів використовують формули скороченого множення, заміну змінної та інші штучні прийоми. Приклад.
Приклад.
3. Невизначеність У цьому випадку і чисельник, і знаменник рекомендується поділити на найбільший степінь змінної, що входить як до знаменника, так і до чисельника. Приклад.
4. Невизначеність Цей тип невизначеності зводиться до невизначеностей Приклад.
Приклад.
Лекція 2 (частина 2) ОСОБЛИВІ ГРАНИЦІ 2.2.4. Перша особлива границя Границі — наслідки першої особливості границі:
1.
Зауваження. За допомогою першої особливої границі можна досліджувати невизначеності
Приклад.
Приклад. Для того щоб скористатися першою особливою границею, потрібно виконати таку заміну змінної х, щоб нова змінна прямувала до нуля, наприклад
Приклад.
2.2.5. Друга особлива границя Границі — наслідки другої особливої границі: 1. Зауваження: За допомогою другої особливої границі та її наслідків можна досліджувати невизначеності
Приклад.
Приклад.
Приклад.
|
|||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 276; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.54.190 (0.009 с.) |

 — послідовність значень аргументу функції з області D; цій послідовності відповідатиме така послідовність значень функції:
— послідовність значень аргументу функції з області D; цій послідовності відповідатиме така послідовність значень функції:  .
. при
при  , якщо для будь-якої послідовності значень аргументу xn,
, якщо для будь-якої послідовності значень аргументу xn, 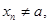 що має границею число а, відповідна послідовність значень функції
що має границею число а, відповідна послідовність значень функції  має границею число b.
має границею число b. для алгебраїчних функцій
для алгебраїчних функцій
 коли порушуються умови теореми про граничний перехід при арифметичних операціях, розв’язання задачі у ряді випадків зводиться до аналізу невизначених виразів виду
коли порушуються умови теореми про граничний перехід при арифметичних операціях, розв’язання задачі у ряді випадків зводиться до аналізу невизначених виразів виду 

 для раціональних функцій
для раціональних функцій називається упорядкованим, якщо
називається упорядкованим, якщо
 на двочлен типу х – а дорівнює значенню многочлена при
на двочлен типу х – а дорівнює значенню многочлена при  тобто
тобто 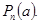
 тобто
тобто  то многочлен
то многочлен  Оскільки
Оскільки  – корінь
– корінь  ділиться без остачі на х – 1. Виконуючи ділення многочленів, дістаємо:
ділиться без остачі на х – 1. Виконуючи ділення многочленів, дістаємо:

 де
де  — такі многочлени, що
— такі многочлени, що 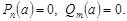


 .
.




 або
або  наприклад, зведенням виразу до спільного знаменника, множенням на спряжений вираз.
наприклад, зведенням виразу до спільного знаменника, множенням на спряжений вираз.


 2.
2.  3.
3.  4.
4. 






 . 2.
. 2.  . 3.
. 3.  . 4.
. 4.  .
. .
.

 .
.


