
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теоритические положения факторного анализа
Факторный анализ (ФА) – методика комплексного и системного изучения и измерения воздействия факторов на величину результативного показателя. Типы ФА: 1. Детерминированный и стохастический 2. Прямой и обратный 3. Одноступенчатый и многоступенчатый 4. Статический и динамический 5. Ретроспективный и перспективный Детерминированный ФА – методика исследования влияния факторов, связь которых с результативными показателями носит функциональный характер. Стохастический ФА – методика исследования факторов, связь которых с рез.показателем является неполной, вероятностой,т.е. корреляционной. При прямом факторном анализе исследование ведется дедуктивным способом (от общего к частному), обратный факторный анализ использует способ логической индукции (от частных факторов обобщающим). Одноступенчатый факторный анализ используется для изучения факторов только одного уровня. При многоступенчатом осуществляется детализация факторов по уровням различной подчинённости. Основные задачи факторного анализа: 1. отбор факторов определяющих результативный показатель 2. классификация и систематизация факторов в целях обеспечения комплексного и системного подхода к исследованию их влияние на результаты хозяйственной деятельности 3. определение формы зависимости между факторами и результативными показателями. Для этого используется теоретический и практический опыт, способы сравнения, корреляции и динамических рядов, аналитических группировок исходной информации, графические. 4. моделирование связей между результативным и факторными показателями. 5. расчет влияния факторов и оценка роли каждого из них изменение величины результативного показателя. 6. работа с факторной моделью, ее практическое использование для управления экономическими процессами. Классификация факторов составляет распределение их по группам в зависимости от общих признаков. По своей природе 1. природно-климатические 2. социально-экономические 3. производственно-экономические. По степени влияния на результаты деятельности 1. основные 2. второстепенные. В зависимости от человека 1. объективные 2. субъективные В зависимости от распространения 1. общие 2. специфические.
По сроку воздействия на результаты хозяйственной деятельности 1. постоянные 2. переменные. По свойствам отражаемых явлений 1. количественные 2. качественные. По составу 1. простые 2. сложные. По характеру действия 1. интенсивные 2. экстенсивные. По возможности измерения влияния 1. измеримые 2. неизмеримые. По местам возникновения 1. Внешние 2. Внутренние
По иерархии 1го, 2го и т.д. уровней. Системный подход в экономическом анализе определяет необходимость взаимосвязанного изучения факторов с учетом всех связей, взаимодействия и соподчиненности. Одним из способов систематизации факторов является формирование детерминированных факторных систем. Создать факторную систему означает представить изучаемое явление в виде алгебраической суммы частного или произведения нескольких факторов, находящихся с ним функциональной зависимости. Совершенствование методики факторного анализа должно быть направлено на взаимосвязанное изучение конкретных факторов, которые по большей части находятся в стохастической зависимости с результативным показателем. При моделировании факторной модели детерминированного характера необходимо выполнить ряд требований: 1. факторы и сами модели должны иметь определенный выраженный характер, реально существовать 2. факторы, входящие в систему, должны быть необходимыми элементами формулы, находится в причинно-следственной связи с изучаемым показателем 3. все показатели факторной модели должны быть количественно измеримых 4. факторная модель должна обеспечивать возможность измерения отдельных факторов. В факторном детерминированном анализе выделяют следующие типы наиболее часто встречающихся моделей: 1. Аддитивные модели результативный показатель представляет собой алгебраическую сумму нескольких факторных показателей 2. Мультипликативные результативный показатель представляет произведение нескольких факторов 3. Кратные результативный показатель получают делением одного факторного показателя на величину другого 4. Смешанные (комбинированные) сочетания различных комбинациях предыдущих моделей.
Для кратных моделей применяют следующие способы их преобразования: 1. Удлинения - удлиняется числитель исходной модели путем замены одного или нескольких факторов на сумму однородных показателей
2. Формального разложения – удлинение знаменателя исходной факторной модели путем замены одного или нескольких факторов на сумму или произведение однородных показателей
3. Расширения – умножение числителя и знаменателя дроби на один или несколько новых показателей
4. Сокращения – создание новой факторной модели путем деления числителя и знаменателя дроби на один и тот же показатель. Моделирование мультипликативных факторных систем в экономическом анализе осуществляется путем последовательного расчленение факторов исходной модели на факторы-сомножители. 3. Способы детерминированного факторного анализа и их характеристика Метод цепных подстановок, индексный, абсолютных и относительных разниц основаны на элиминировании. Метод цепных подстановок используется для анализа влияния факторов во всех типах детерминированных факторных моделей. Этот способ позволяет определить влияние отдельных факторов на изменение величины результативного показателя путем постепенной замены базисной величины каждого показателя в объеме результативного показателя на фактические в отчётном периоде. С этой целью определяется ряд условных величин результативного показателя (подстановки), которые учитывают изменение одного, затем двух и так далее факторов, допуска, что остальные не меняются. Сравнение величины результативного показателя до и после уровня того или другого фактора позволяет элиминироваться от влияния всех факторов, кроме одного, и определить воздействие последнего на прирост результативного показателя. Способ цепной подстановки имеет следующую последовательность реализации: 1. необходимо учитывать изменения количественных, а затем качественных показателей. 2. если имеется несколько количественных и качественных показателей, необходимо сначала измерить величину факторов первого уровня, а за тем более низкого. Индексный метод основан на относительных показателях динамики, пространственных сравнениях, выполнения плана, выражает отношение уровня определенного явления к его уровням в прошедшем периоде. Индексы, которые выражают отношения непосредственно измеряемых величин, называются индивидуальными. Те, которые характеризуют соотношение сплошных явлений, называются групповыми. С помощью агрегатных индексов выявляется влияние различных факторов на изменение уровня результативных показателей в мультипликативных и кратных моделях. Метод абсолютных разниц применяется для определения влияния отдельных факторов на результативный показатель в мультипликативных и мультипликативно-аддитивных моделях. Его суть состоит в последовательном исчислении разницы между частными показателями и определении влияния этой разницы на обобщающие показатели при неизменных других частных показателях. Метод относительных разниц применяется для измерения влияния факторов в тех случаях, когда исходные данные содержит уже определенные ранее относительные отклонения факторных показателей в процентах или коэффициентах. Для расчета влияние первого фактора необходимо базисную величину результативного показателя умножить на относительный прирост первого фактора, выраженного в процентах, а результат разделить на 100.
Для определения влияния второго фактора к базисной величине результативного показателя прибавляют его изменение за счет первого фактора, а полученную сумму умножают на относительный прирост второго фактора в процентах или коэффициентах. Результат делится на 100. Влияние всех последующих фактор определяется аналогично. Данный метод следует применять в моделях, имеющих большой комплекс факторов. Способ пропорционального деления используется для определения величины влияния факторов на прирост результативного показателя в ряде случаев. Например, при анализе рентабельности. Недостатком вышеперечисленных методов является возникновение неразложимого остатка, который присоединяется к числовому значению влияние последнего фактора, то есть последовательность включения факторов в модель влияет на величину влияния факторов. Этим недостатком не обладает интегральный метод, используемый в детерминированном факторном анализе. Он позволяет получить более точные результаты в мультипликативных, кратных и смешанных моделях, а так же избежать неоднозначные оценки влияния факторов. Метод логарифмирования применяется для изменения влияния факторов в мультипликативных моделях. Логарифмирование является более точным при подсчете влияния факторов: в данном случае результативное совместное действие факторов распространяется пропорционально доли изолированного влияния каждого фактора на уровень результативного показателя. При логарифмировании используются индексы роста или снижения результативных показателей. И общий прирост результативного показателя распространяется по факторам пропорционально отношению логарифмов факторных индексов к логарифму индекса результативного показателя. 4.Способы стохастического факторного анализа. Корреляционная (стохастическая) связь - это неполная вероятностная зависимость между показателями, которая проявляется только в массе наблюдений. Отличают парную и множественную корреляцию. Парная корреляция - это связь между двумя показателями. Один – факторный, а другой - результативный. Множественная корреляция возникает от взаимодействия нескольких факторов с результативными показателями.
Для анализа стохастической зависимости используются следующие способы: 1. сравнение параллельных и динамических рядов 2. аналитической группировки 3. корреляционно-регрессионный, дисперсионный, компонентный, кластерный анализ и другое. Условия применения корреляционного анализа: 1. наличие достаточно большого количества наблюдений по величине исследуемых факторов 2. исследуемые факторы должны иметь количественное измерение и отражаться в источниках информации. Для измерения тесноты связи между факторными и результативными показателями определяется коэффициент корреляции (в случае прямолинейной зависимости). Коэффициент корреляции (r) и ŋ характеризуют количественную оценку тесноты связи. В зависимости от их величины теснота связи подразделяется: 1. слабая (от 0,1 до 0,3) 2. умеренная (от 0,3 до 0,5) 3. заметная (от 0,5 до 0,7) 4. высокая (от 0,7 до 0,9) 5. весьма высокая (от 0,9до 0,99) Если r возвести в квадрат, получим коэффициент детерминации. Он показывает, чему равна доля влияния изучаемого факторов на результативный показатель. При значительной тесноте связи величина индекса детерминации всегда меньше 50%. Это означает, что на долю вариации факторного признака приходится меньшая по сравнению с другими признаками, влияющими на результативный показатель. Синтезированные при таких условиях математические модели связи практического значения не имеют. Множественная корреляция применяется в тех случаях, когда придерживаться правил по отбору факторов, включаемых в модель: 1. следует учитывать причинно-следственные связи между показателями 2. необходимо отбирать только самые значимые факторы, оказывающие влияние на результативный показатель. Следует обратить внимание только на факторы, которые имеют критерии надежности по Стьюденту больше табличных. 3. все факторы должны быть количественно измеримы. 4. не рекомендуется включать в модели взаимосвязанные основные факторы 5. модель линейного типа не должна включать факторы, связь которых с результативным признаком имеет криволинейный характер. Последовательность проведения анализа многофакторного корреляционного анализа: 1. определите факторы, которые оказывают воздействие на изучаемый показатель и отобрать наиболее существенные 2. собрать и оценить исходную информацию, необходимую для корреляционного анализа 3. изучить характер и моделировать связь между факторами и результативным показателем 4. провести расчет основных показателей связи корреляционного анализа 5. провести статистическую оценку результатов корреляционного анализа и их практическое применение 5. Методы оптимизационного решения экономических задач Среди способов оптимизации показателей наибольшее применение нашли: 1. экономико-математические методы 2. экспертных оценок специалистов 3. программирование 4. теория массового обслуживания
5. теория игр 6. исследование операций. Экспертные оценки специалистов Представляет собой обобщение оценок экспертов, касающихся перспектив развития того или иного экономического субъекта. Особенностями метода включается в последовательном, индивидуальном, анонимном опросе экспертов. Цель метода – выявить производственные факторы, существенно влияющие на те или иные показатели, опираясь на знания, компетенцию ученых-практиков, опыт работы. Метод экспертных оценок реализуется в следующей последовательности: 1. Отбираются факторы, по которым будет проводится оценка; 2. Определяется число экспертов, которые будут проводить оценку; 3. Устанавливается бальная шкала оценок: меньший по значению ранг присваивается фактору, который имеет наибольшее влияние на результативный показатель; 4. Оценки каждого из экспертов заносят в специальную таблицу – матрицу рангов опроса; 5. На основании полученных оценок рассчитывают суммы значений рангов по каждому фактору и среднее арифметическое значение суммы рангов опросов; 6. Определяется разность между суммой значений рангов опросов по каждому фактору и средним арифметическим значениям суммы рангов опроса; 7. Результатом вычислений определяется степень согласованности мнений экспертов.
W –это степень согласованности мнений экспертов m –это число экспертов N–количество факторов, взятых для оценки W<0,3 – согласованность мнений неудовлетворительная 0,3<W<0,7 – согласованность средняя W>0,7 – согласованность высокая
Методы программирования являются основными средствами решения задач оптимизации производственно-хозяйственной деятельности. Эти методы позволяют оценивать напряженность плановых заданий, получать оценки дефицитности ресурсов. Методы линейного программирования основаны на решение системы линейных уравнений, когда зависимость между изучаемыми явлениями строго функциональная. Для линейного программирования характерно математическое выражение переменных величин, определенный порядок, алгоритмы, логический анализ. Методы динамического программирования применяются при решении оптимизационных задач, когда целевая функция и ограничения одновременно характеризуются нелинейными зависимостями. Признаки нелинейности – наличие переменных, указатели которых отличаются от 1, а также наличие переменных, показателей степени под корнем, под знаком логарифма. Под исследованием операций понимается разработка методов, количественная оценка полученных решений и выбор из них наилучшего. Предметом исследования операций являются экономические системы, в том числе производственно-хозяйственная деятельность предприятий. Целью является такое сочетание структурных взаимосвязанных элементов системы, в которых в наибольшей степени отвечают задачей получения наилучшего экономического показателя из ряда возможных. Теория игр теория математических моделей принятия оптимальных решений в условиях неопределённости или конфликта нескольких сторон, имеющих различные интересы. Она исследует оптимальные стратегии в ситуациях игрового характера. К ним относятся ситуации, связанные с выбором выгодных производственных условий, организации статистического контроля качества, хозяйственных взаимоотношений между предприятиями промышленности и других отраслей. Теории игр может использоваться для выбора оптимальных решений при создании рациональных запасов сырья, материалов, полуфабрикатов. Теория массового обслуживания Исследует на основе теории вероятности математические методов количественной оценки процессов массового обслуживания. Общей особенностью всех задач, связанных с массовым обслуживанием является случайный характер исследуемых явлений, а решение при помощи методов теории вероятностей позволяет пояснить и решить те проблемы, которые формируются в процессе обслуживания.
|
|||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 266; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.87.156 (0.067 с.) |

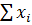 –это сумма значений рангов по каждому фактору
–это сумма значений рангов по каждому фактору – среднее арифметическое значение суммы рангов
– среднее арифметическое значение суммы рангов


