
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теплогидравлический расчет магистрального нефтепроводаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
14.6.1 Используемые для расчетов переменные, их обозначения и единицы измерения приведены в таблице 14.14. Таблица 14.14 - Принятые обозначения переменных используемых для расчетов
Окончание таблицы 14.14
14.6.1.2 Используемые в расчетах безразмерные параметры и формулы для их расчета: -число Рейнольдса, критерий режима движения жидкости:
-число Нуссельта, безразмерный коэффициент теплоотдачи:
где: l - характерный размер; -параметр Грасгофа, критерий подобия процессов свободной конвекции:
где -параметр Прандтля, критерий подобия полей температур и скоростей:
- параметр Шухова:
14.6.2 Параметры транспортируемой нефти 14.6.2.1 Необходимые для выполнения теплогидравлических расчетов параметры нефти или смеси разных сортов нефти должны определяться экспериментально во всем предполагаемом диапазоне значений влияющих на эти параметры факторов (температуры, давления, скорости сдвига, содержания воды и др.). Число измерений 14.6.2.2 Значение плотности при температуре
Величина коэффициента объемного расширения b выбирается из справочников. 14.6.2.3 Исходными данными для определения параметров модели течения жидкости являются результаты лабораторных измерений напряжения сдвига для нефти при различных скоростях сдвига и температурах (см. таблицу 14.15). Таблица 14.15 – Результаты лабораторных измерений напряжения сдвига
На основе этих данных определяются параметры модели течения жидкости при каждой температуре в соответствии с п.14.6.2.5. 14.6.2.4 Если во всем диапазоне температур жидкость следует ньютоновской модели течения, то достаточно иметь измерения только абсолютной или кинематической вязкости Кинематическая вязкость,
14.6.2.5 Модель течения жидкости задается уравнением Таблица 14.16 – Модели течения жидкости
Параметры модели Параметры модели определяются по следующим формулам ( а) Параметр
б) Параметры
в) Параметры
г) Параметры
Параметр
принимало минимальное значение. Выбор модели течения осуществляется по двум критериям: сумме квадратов отклонений и риску (под риском понимается эмпирическая оценка возможности принятия более сложной модели течения вместо более простой модели). Сумма квадратов отклонений рассчитывается по формуле:
где
Для нахождения риска применяется следующая оценка, предложенная в работе [16]:
где
Если выражение в квадратных скобках в формуле (14.52) обозначить через
Выбор модели течения производится из моделей, для которых риск не равен бесконечности. Анализ формул (14.52), (14.53) для оценки риска показывает, что риск принимает бесконечно большое значение, если объем выборки менее трех точек для ньютоновской (однопараметрической) модели, менее семи точек для двухпараметрической модели (степенная модель и модель Шведова – Бимгама), менее одиннадцати точек для трехпараметрической модели (модель Гершеля – Бакли). Таким образом, для того, чтобы данная модель не была отброшена из рассмотрения, необходимо, чтобы объем выборки был не менее указанных значений. Для выбора модели течения нефти при фиксированной температуре необходимо для каждой модели определить значения аддитивного критерия, объединяющего критерии суммарной погрешности и риска. Для этого полученные значения критериев необходимо предварительно нормировать по формулам:
где: Нормировка значений критерия риска производится по значениям этого критерия, не равным бесконечности. Модели течения, для которых риск равен бесконечности, при выборе модели не рассматриваются. При фиксированной температуре, выбирается модель течения, для которой выполняется условие минимума аддитивного критерия:
Параметры 14.6.2.6 Для удобства последующих расчетов зависимости
Здесь
Поскольку при найденных указанным способом коэффициентах минимизируется не сумма квадратов отклонений расчетных величин от измеренных значений параметра, а сумма квадратов разности логарифмов этих значений, то качество аппроксимации может оказаться неудовлетворительным. В этом случае найденные коэффициенты следует рассматривать как первое приближение и скорректировать их вручную. 14.6.2.7 При отсутствии экспериментальных данных о вязкости смеси для ориентировочного расчета вязкости смеси можно использовать формулу (см. [12]):
где:
14.6.2.8 В случае смешения нефти нескольких сортов с разными значениями плотности
где
14.6.3 Постановка задач 14.6.3.1 Рассматривается трубопровод, который может иметь участки как подземной, так и надземной прокладки. Участки нефтепровода могут быть с тепловой изоляцией и/или попутным электроподогревом. Может предусматриваться подогрев нефти в начале нефтепровода и в промежуточных пунктах. 14.6.3.2 Решаются задачи: - расчет потерь напора на трение и распределение температуры нефти по длине трубопровода в установившемся (тепловом и гидравлическом) режиме перекачки; - расчет изменения температуры нефти в трубопроводе в переходном процессе после остановки перекачки. 14.6.3.3 Принятые допущения Гидравлический расчет стационарного режима перекачки выполняется по обычным формулам гидравлики. При этом в расчетах используется эффективная динамическая вязкость, рассчитываемая по формуле:
а скорость сдвига по формуле:
14.6.3.4 При расчете стационарного теплового режима: - учитывается превращение работы по преодолению внутреннего трения в тепло, теплоотдача от трубопровода в окружающую среду, а также транспорт тепла перекачиваемой нефтью; - плотность транспортируемой нефти вдоль трубопровода считается зависящей только от температуры; - параметры модели течения - температура окружающей среды (грунта) для подземного трубопровода принимается равной температуре грунта в ненарушенном тепловом состоянии на глубине оси нефтепровода в соответствующий сезон; - теплопередача через стенку трубопровода в продольном направлении не учитывается. 14.6.3.5 При расчете остывания нефтепровода после остановки перекачки: - рассматривается нестационарный процесс теплопередачи в нефти, температура окружающей среды (грунта) принимается неизменной во времени; - температура грунта принимается равной температуре наружной поверхности трубопровода (включая изоляцию), определенной при расчете стационарного тепло-гидравлического режима; - теплопередача в продольном направлении через стенку трубопровода и через нефть не учитывается. 14.6.4 Расчет стационарного тепло-гидравлического режима 14.6.4.1 Для расчета температуры и потерь напора на трение нефтепровода разбивается на элементарные участки длиной L. Длина участка определяется исходя из требований: - диаметры D2, D3 неизменны по всей длине участка; - на участке отсутствуют попутные сбросы/подкачки нефти, а также подключения лупингов; - климатические факторы (температура грунта, окружающего воздуха, количество осадков) и характеристики грунтов изменяются вдоль участка незначительно; - получаемая в результате расчета температура в конце участка отличается от температуры в начале участка не более чем на 0,1°С. 14.6.4.2 Потери напора на трение на рассматриваемом участке определяются по формуле Дарси-Вейсбаха:
а температура нефти в конце участка по формуле Шухова –Лейбензона:
где поправка на нагрев нефти за счет внутреннего трения:
14.6.4.3 Коэффициент гидравлического сопротивления определяется в зависимости от режима течения (числа Рейнольдса) по формулам:
Эквивалентная шероховатость труб принимается на основе справочных данных [2]. 14.6.4.4 Средняя скорость потока нефти в трубопроводе определяется по формуле:
а число Рейнольдса - по формуле (14.36) Плотность и вязкость нефти приводятся к температуре нефти в начале участка в соответствии с 14.6.2 настоящего документа. 14.6.4.5 Отнесенный к одному погонному метру внутренней поверхности трубы коэффициент теплопередачи от нефти к цилиндрической поверхности, контактирующей с окружающей средой, определяется по формуле:
Термическое сопротивление стенки трубы, антикоррозионной и тепловой изоляции определяется по формуле:
14.6.4.6 Коэффициент внутренней теплоотдачи от нефти к внутренней стенке трубопровода вычисляется по формуле:
Параметр Нуссельта определяется в соответствии с формулами [18]:
14.6.4.7 Коэффициент внешней теплоотдачи для подземных участков трубопровода от наружной поверхности трубопровода (с учетом тепловой изоляции при ее наличии) к воздуху определяют по формуле:
где приведенная глубина залегания оси трубопровода вычисляется по формулам:
при отсутствии снегового покрова и
при наличии снегового покрова. При определении k и Коэффициент

Рисунок 14.1 - Коэффициент теплоотдачи Для надземных участков трубопровода коэффициент теплоотдачи 14.6.4.8 После определения температуры нефти
14.6.5 Решение задачи остановки (остывания) трубопровода 14.6.5.1 Задача остывания нефти в элементарном участке трубопровода, рассматриваемом в 14.6.4 настоящего документа, и в условиях принятых допущений 14.6.3.3 настоящего документа, описывается уравнением теплопроводности в частных производных в одномерной постановке. Температура
Данное уравнение решается для каждого из элементарных участков независимо друг от друга. 14.6.5.2 Граничные условия для решения уравнения теплопроводности:
где: Коэффициент теплопередачи от нефти к наружной стенке трубы (изоляции) определяется по формуле:
Коэффициент
где: коэффициенты Таблица 14.18 - Коэффициенты для расчета параметра Нуссельта
Число Прандтля определяется по формуле:
Число Грасгофа определяется по формуле:
где:
Вязкость и плотность нефти при расчете параметров Второе граничное условие сформулировано, исходя из того, что в течение относительно короткого времени остывания (допустимое время остановки трубопровода 72 часа) температура грунта вокруг трубопровода практически не изменится. 14.6.5.3 Начальными условиями для данного уравнения являются: распределение температуры нефти в начале элементарного участка, распределение температуры внутренней стенки трубопровода и температуры наружной стенки трубопровода или наружной стенки изоляции (при ее наличии): - равенство температуры по всему проходному сечению температуре нефти
- равенство температуры внутренней стенки трубопровода ее температуре
14.6.5.4 Решение уравнения теплопроводности Для численного решения уравнения проходное сечение трубопровода представляется рядом окружностей с безразмерными радиусами, изменяющимися на заданную величину (шаг по радиусу Шаг по времени рекомендуется принимать равным 1 часу = 3600 с. Число точек по времени (не считая точки
Шаг по радиусу является безразмерным, рекомендуется принять его равным 1/40 внутреннего диаметра трубы. Количеством точек деления по радиусу (не считая точки
Безразмерный радиус
Все возможные сочетания указанных окружностей и моментов времени являются расчетными точками в пространстве радиус окружности – момент времени. В этом пространстве уравнение теплопроводности и граничные условия заменяются разностными схемами. Разностная аппроксимация уравнения (14.81) будет следующей:
где: распределение температур в каждом i-м сечении определяется последовательно, от стенки к центру по следующим реккурентным формулам:
где
Разностная аппроксимация граничных
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 903; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.28.217 (0.013 с.) |

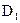


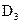



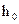






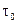
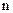

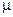

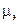
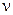
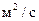



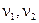
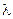


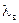


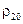

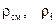

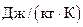

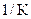
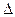

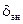




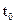
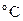







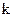


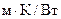
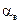


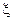


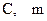
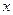 (напряжение сдвига, вязкость, показатель степени в реологической модели) от температуры экспоненциальной функцией
(напряжение сдвига, вязкость, показатель степени в реологической модели) от температуры экспоненциальной функцией 


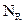 ,
, 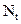
 ,
, 


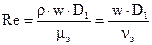 ; (14.36)
; (14.36) , (14.37)
, (14.37) , (14.38)
, (14.38)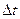 - разность между средней температурой нефти вблизи поверхности теплообмена и температурой поверхности теплообмена (внутренней стенки трубопровода);
- разность между средней температурой нефти вблизи поверхности теплообмена и температурой поверхности теплообмена (внутренней стенки трубопровода); ; (14.39)
; (14.39)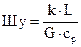 (14.40)
(14.40)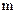 в этом диапазоне должно быть не меньше 10.
в этом диапазоне должно быть не меньше 10. выполняется при известном значении
выполняется при известном значении  по формуле:
по формуле: (14.41)
(14.41)
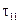


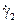

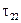



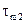

 (14.42)
(14.42) (модель Гершеля - Бакли). Частными случаями этой модели являются модели Ньютона
(модель Гершеля - Бакли). Частными случаями этой модели являются модели Ньютона 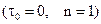 , Шведова – Бингама
, Шведова – Бингама  и Оствальда – де Ваале
и Оствальда – де Ваале  . Уравнения этих моделей приведены в таблице 14.16. Все модели, кроме модели Ньютона, являются моделями неньютоновских жидкостей. Сложностью модели является количество ее параметров.
. Уравнения этих моделей приведены в таблице 14.16. Все модели, кроме модели Ньютона, являются моделями неньютоновских жидкостей. Сложностью модели является количество ее параметров.
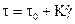
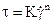

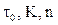 определяются в результате обработки ряда значений
определяются в результате обработки ряда значений  и
и  , измеренных при фиксированной температуре.
, измеренных при фиксированной температуре.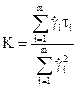 (14.43)
(14.43) (14.44)
(14.44)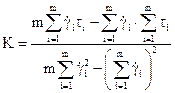 (14.45)
(14.45) (14.46)
(14.46)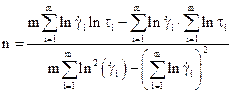 (14.47)
(14.47) (14.48)
(14.48)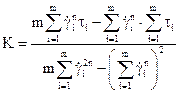 (14.49)
(14.49)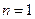 ) таким образом, чтобы значение функции:
) таким образом, чтобы значение функции: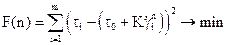 (14.50)
(14.50)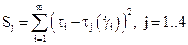 , (14.51)
, (14.51)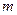 - количество замеров напряжения сдвига при фиксированной температуре;
- количество замеров напряжения сдвига при фиксированной температуре; - экспериментальные значения (данные, полученные с вискозиметра);
- экспериментальные значения (данные, полученные с вискозиметра);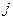 - номер модели течения;
- номер модели течения; - функция модели течения.
- функция модели течения.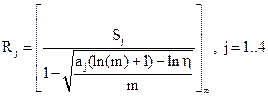 (14.52)
(14.52)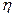 - вероятность того, что риск будет меньше либо равен полученной его оценки. Согласно рекомендациям, изложенным в [16], принимается значение
- вероятность того, что риск будет меньше либо равен полученной его оценки. Согласно рекомендациям, изложенным в [16], принимается значение  ;
;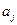 - количество параметров модели
- количество параметров модели  , то результат вычисления риска принимает следующие значения:
, то результат вычисления риска принимает следующие значения: (14.53)
(14.53)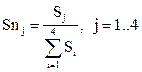 (14.54)
(14.54) (14.55)
(14.55) - номер модели течения.
- номер модели течения. (14.56)
(14.56) выбранной по описанному алгоритму модели используются для расчета эффективной динамической вязкости (см. 14.6.3.3 настоящего документа).
выбранной по описанному алгоритму модели используются для расчета эффективной динамической вязкости (см. 14.6.3.3 настоящего документа). ,
, 
 ,
, 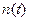 аппроксимируются экспоненциальными функциями:
аппроксимируются экспоненциальными функциями: (14.57)
(14.57)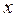 - параметр, зависимость которого от температуры аппроксимируется,
- параметр, зависимость которого от температуры аппроксимируется,  - коэффициенты аппроксимации. Для определения этих коэффициентов правая и левая части (14.79) логарифмируются, и коэффициенты определяются методом наименьших квадратов:
- коэффициенты аппроксимации. Для определения этих коэффициентов правая и левая части (14.79) логарифмируются, и коэффициенты определяются методом наименьших квадратов: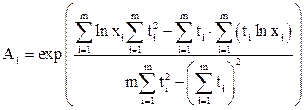 (14.58)
(14.58) (14.59)
(14.59)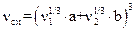 , (14.60)
, (14.60) - массовые концентрации компонент в смеси.
- массовые концентрации компонент в смеси. , плотность смеси определяется по следующей формуле:
, плотность смеси определяется по следующей формуле: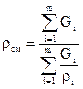 , (14.61)
, (14.61) - массы смешиваемых компонент;
- массы смешиваемых компонент;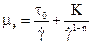 , (14.62)
, (14.62) . (14.63)
. (14.63) и
и  , (14.64)
, (14.64)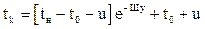 , (14.65)
, (14.65) (14.66)
(14.66) при ламинарном режиме (
при ламинарном режиме (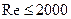 ), (14.67)
), (14.67) для всех зон турбулентного режима (
для всех зон турбулентного режима (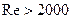 ) (14.68)
) (14.68) , (14.69)
, (14.69) (14.70)
(14.70) . (14.71)
. (14.71) (14.72)
(14.72) при
при  при
при  (14.74)
(14.74) при
при  (14.75)
(14.75) , (14.76)
, (14.76) (14.77)
(14.77) (14.78)
(14.78)
 поверхности трубопровода по формулам (см. [15]):
поверхности трубопровода по формулам (см. [15]): , (14.79)
, (14.79) (14.80)
(14.80)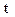 нефти в элементарном участке является симметричной относительно оси нефтепровода функцией расстояния R
нефти в элементарном участке является симметричной относительно оси нефтепровода функцией расстояния R 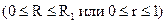 рассматриваемой точки от оси трубопровода и времени
рассматриваемой точки от оси трубопровода и времени  от момента остановки трубопровода:
от момента остановки трубопровода: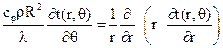 (14.81)
(14.81) (14.82)
(14.82)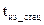 - температура наружной стенки трубы (включая все слои изоляции при ее наличии), полученная при тепло-гидравлическом расчете стационарного режима для начала данного элементарного участка, находящегося на расстоянии z от начала трубопровода (14.6.4 настоящего документа).
- температура наружной стенки трубы (включая все слои изоляции при ее наличии), полученная при тепло-гидравлическом расчете стационарного режима для начала данного элементарного участка, находящегося на расстоянии z от начала трубопровода (14.6.4 настоящего документа). (14.83)
(14.83) по формуле:
по формуле: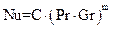 , (14.84)
, (14.84) и
и 






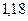
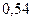
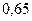
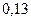


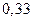
 (14.85)
(14.85) , (14.86)
, (14.86) - средняя температура нефти в рассматриваемом сечении;
- средняя температура нефти в рассматриваемом сечении; - температура внутренней поверхности трубопровода в рассматриваемом сечении.
- температура внутренней поверхности трубопровода в рассматриваемом сечении. и
и  должна определяться при температуре, определяемой как среднее значение между средней температурой нефти в рассматриваемом сечении и температурой внутренней поверхности трубопровода в том же сечении.
должна определяться при температуре, определяемой как среднее значение между средней температурой нефти в рассматриваемом сечении и температурой внутренней поверхности трубопровода в том же сечении.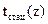 , полученной при тепло-гидравлическом расчете стационарного режима для данного элементарного участка:
, полученной при тепло-гидравлическом расчете стационарного режима для данного элементарного участка: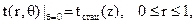 (14.87)
(14.87) , полученной при тепло-гидравлическом расчете стационарного режима для данного элементарного участка:
, полученной при тепло-гидравлическом расчете стационарного режима для данного элементарного участка: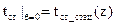 (14.88)
(14.88) ) до значения
) до значения  . Эти окружности и точка, лежащая на оси трубы, являются расчетными точками. Время протекания переходного процесса также представляется в виде ряда моментов, каждый из которых отстоит от предыдущего (начиная с момента начала переходного процесса) на постоянную величину
. Эти окружности и точка, лежащая на оси трубы, являются расчетными точками. Время протекания переходного процесса также представляется в виде ряда моментов, каждый из которых отстоит от предыдущего (начиная с момента начала переходного процесса) на постоянную величину 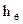 – шаг по времени.
– шаг по времени. ) определяется по заданному времени остывания
) определяется по заданному времени остывания 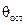 и шагу по времени из соотношения:
и шагу по времени из соотношения: (14.89)
(14.89) ) связано с шагом соотношением:
) связано с шагом соотношением: (14.90)
(14.90)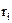 определяется по номеру точки деления как
определяется по номеру точки деления как (14.91)
(14.91) , (14.92)
, (14.92) , (14.93)
, (14.93)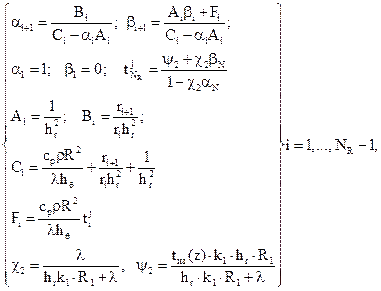 (14.94)
(14.94)


