
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Гидравлический расчет технологических трубопроводов с учетом местных сопротивленийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте 5.6.1 Гидравлическими расчетами определяются суммарные потери напора в трубопроводах, в том числе: потери напора на трение, потери напора на местные сопротивления, потери скоростного напора и потери преодоления разности геодезических отметок конца и начала трубопровода или его участка. 5.6.2 Гидравлические расчеты производятся исходя из объемного расхода, диаметра и длины расчетного участка трубопровода, физических характеристик перекачиваемой нефти или нефтепродукта, разности геодезических отметок начала и конца расчетного участка и наличия местных сопротивлений на участке. 5.6.3 Суммарные потери напора на расчетном участке измеряются в метрах и определяются по формуле:
где: hтр – потери напора на трение, м; hмс – потери напора на преодоление местных сопротивлений, м; Dz=z2-z1 – алгебраическая разность геодезических отметок конца z2 и начала z1 расчетного участка, м; hск – потери скоростного напора на расчетном участке (см. формулу (5.48)), м. 5.6.4 Потери напора на трение. Потери напора на трение определяются по формуле:
где: i – гидравлический уклон, м/км; L – длина расчетного участка, км. 5.6.4.1 Гидравлический уклон определяется по уравнению гидравлики:
где: λ – коэффициент гидравлического сопротивления; d – внутренний диаметр трубопровода, м; W – скорость движения жидкости в трубопроводе, м/с; g – ускорение силы тяжести, м/с2. В практике проектирования принято измерение гидравлического уклона в м/км для магистральных трубопроводов и в м/м для технологических трубопроводов. Соответственно длина трубопровода также подставляется в формулы в километрах либо метрах. 5.6.4.2 Коэффициент гидравлического сопротивления зависит от режима движения жидкости по трубопроводу, который определяется в зависимости от значения параметра Рейнольдса:
где: n – кинематическая вязкость жидкости, м2/с. 5.6.4.3 При значениях Re до 2300 режим движения жидкости является ламинарным (струйным) и коэффициент гидравлического сопротивления определяется по формуле:
5.6.4.4 При значениях Re от 2300 до 2800, характеризующих переходный режим от ламинарного к турбулентному, коэффициент гидравлического сопротивления определяется по формуле:
5.6.4.5 При значениях Re более 2800 режим движения жидкости является турбулентным. Формулы для определения коэффициента гидравлического сопротивления при этом режиме для разных чисел Рейнольдса и предельные максимальные значения Re, ограничивающие область применения этих формул для труб различных диаметров, приводятся в таблицах 5.16 и 5.17. Таблица 5.16 - Формулы определения коэффициентов гидравлического сопротивления для цельнотянутых труб
Окончание таблицы 5.16
Таблица 5.17 - Формулы определения коэффициентов гидравлического сопротивления для сварных труб
5.6.5 Потери напора на преодоление местных сопротивлений 5.6.5.1 Потери напора на преодоление местных сопротивлений определяются исходя из значения коэффициентов местных сопротивлений и расчетной скорости движения жидкости:
где: ξ – коэффициент местного сопротивления, определяемый по таблице 5.18. Таблица 5.18 - Значения коэффициентов местных сопротивлений технологических трубопроводов
Окончание таблицы 5.18
5.6.5.2 Величины коэффициентов местных сопротивлений, приведенные в таблице, получены на основе систематизации, анализа и обработки данных по ним в технической литературе. 5.6.5.3 При определении потерь напора в местных сопротивлениях расчетная величина скорости W должна приниматься равной скорости в трубе за местным сопротивлением. 5.6.5.4 Общие потери напора на преодоление местных сопротивлений технологического трубопровода определяются суммой потерь по всем n местным сопротивлениям:
5.6.5.5 В зависимости от того, какие виды сопротивлений линейные или местные преобладают в конкретной трубопроводной системе, для проведения приближенных оценочных расчетов может применяться обобщение путем приведения потерь имеющих меньший вклад к эквивалентным потерям доминирующего вида, что упрощает расчеты. 5.6.5.6 Так возможно представление совокупных потерь на преодоление местных сопротивлений, выражаемых формулой (5.40) через линейные потери, выражаемые формулой (5.36) и соответствующую длину трубопровода, эквивалентную местным сопротивлениям:
5.6.5.7 Формула (5.42) может быть выражена также и через величину гидравлического уклона:
5.6.5.8 С помощью эквивалентной длины расчет потерь на трение в трубопроводе с местными сопротивлениями может быть сведен к расчету потерь на трение в прямой трубе, приведенная длина которой:
где: LГ – геометрическая длина трубопровода, м. 5.6.5.9 Аналогично возможно представление совокупных линейных потерь в виде эквивалентного по величине местного сопротивления:
5.6.5.10 Формула 5.45 может быть выражена также и через величину гидравлического уклона:
5.6.5.11 С помощью эквивалентного местного сопротивления в расчете потерь на трение в трубопроводе возможно не учитывать в явном виде протяженные участки и оперировать только с приведенной суммой местных сопротивлений:
где: 5.6.5.12 При использовании формул (5.42), (5.45) следует учитывать что поскольку коэффициент λ зависит от расхода Q в трубопроводе, удовлетворительные результаты данный метод оценки имеет только в турбулентном режиме течения жидкости. 5.6.6 Потери скоростного напора. 5.6.6.1 Потери скоростного напора на расчетном участке трубопровода определяются по формуле:
где: W2 – скорость в конце расчетного участка, м/с; W1 – скорость в начале расчетного участка, м/с.
Диаграмма 1
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 729; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

 , (5.34)
, (5.34) , (5.35)
, (5.35) , (5.36)
, (5.36) , (5.37)
, (5.37) (5.38)
(5.38) (5.39)
(5.39) при Re до:
при Re до:
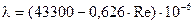

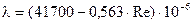








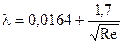
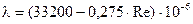




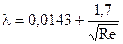

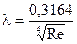 при значениях Re до:
при значениях Re до:

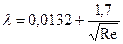
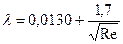



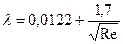
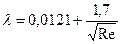


 , (5.40)
, (5.40)
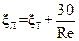
















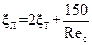






















 (5.41)
(5.41)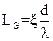 (5.42)
(5.42) (5.43)
(5.43) , (5.44)
, (5.44) (5.45)
(5.45) (5.46)
(5.46) , (5.47)
, (5.47) – сумма местных сопротивлений трубопровода.
– сумма местных сопротивлений трубопровода. , (5.48)
, (5.48)


