
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Возрастание и убывание функций. Экстремумы функции
Функция
Функция
рис.1 рис.2 Теорема. Если в данном промежутке Теорема имеет простой геометрический смысл. Если в некотором промежутке касательная к графику функции Интервалы, на которых функция только возрастает или же только убывает, называются интервалами монотонности функции, а сама функция называется монотонной на этих интервалах. Геометрически ясно, что функция будет монотонной и в том случае, когда её производная, сохраняя всё время постоянный знак, обращается в отдельных точках в нуль, касательная в которых параллельна оси Например, функция Экстремумы функций. Точка Другими словами, максимумом (минимумом) функции Если в точке Необходимое условие экстремума. Если точка Точки, в которых производная равна нулю или не существует, называются критическими точками. Однако не всякая критическая точка является точкой экстремума, поэтому необходимо в каждой критической точке проверить, выполняется ли достаточное условие экстремума.
Первое достаточное условие экстремума функции. Пусть функция Другими словами, если Второе достаточное условие экстремума функции. Критическая точка Например, пусть выполнены условия если если Пример 1. Исследовать на экстремум функцию
Решение. Областью определения данной функции является вся числовая прямая. Находим производную данной функции: Решаем это уравнение:
Находим критические точки: Рассмотрим интервалы: Выбираем внутри каждого из этих интервалов произвольную точку и определяем знак первой производной, используя уравнение (*). Результаты удобно оформить в виде рисунка.
Итак, в точке Пример2. Исследовать на экстремум функцию
Решение. Область определения данной функции: Находим первую производную: Тогда при
Для выяснения характера критических точек воспользуемся вторым достаточным условием экстремума. Находим вторую производную: Определяем знак второй производной в критических точках: Исследование функций на выпуклость и вогнутость. График функции
рис. 1 рис. 2 Достаточное условие выпуклости (вогнутости) графика функции. Пусть Точка Необходимое условие точки перегиба. Если Точки, в которых вторая производная равна нулю или не существует, называются критическими точками II-го рода. Достаточное условие точки перегиба. Пусть функция Другими словами, если при переходе через критическую точку Асимптотой кривой называется прямая, к которой неограниченно приближается точка кривой при неограниченном удалении её от начала координат. 1. Прямая 2. Прямая
или
Частным случаем наклонной асимптоты при 3. Прямая Пример 1. Найти точки перегиба и промежутки выпуклости и вогнутости функции Решение. Область определения функции – вся числовая прямая. Находим производные:
Приравняв к нулю вторую производную, получим критические точки второго рода:
Отметив точку
Таким образом, на интервале Пример2. Найти асимптоты кривой Решение. Область определения функции Ищем вертикальные асимптоты:
Следовательно, прямая Горизонтальных асимптот нет, так как
т.е. оба предела не существуют (при вычислении пределов использовалось правило Лопиталя).
Ищем наклонные асимптоты:
т.е. Следовательно, прямая
Рис. 3
|
|||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 315; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.196.217 (0.05 с.) |
 называется возрастающей в некотором промежутке
называется возрастающей в некотором промежутке  , если для любых двух значений
, если для любых двух значений  и
и  , принадлежащих этому промежутку, из неравенства
, принадлежащих этому промежутку, из неравенства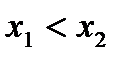 следует неравенство
следует неравенство  (рис.1)
(рис.1) называется убывающей в некотором промежутке, если для любых двух значений
называется убывающей в некотором промежутке, если для любых двух значений  и
и  , принадлежащих этому промежутку, из неравенства
, принадлежащих этому промежутку, из неравенства следует неравенство
следует неравенство  (рис.2)
(рис.2)

 , то функция возрастает в этом промежутке; если же
, то функция возрастает в этом промежутке; если же 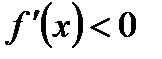 , то функция убывает в соответствующем промежутке.
, то функция убывает в соответствующем промежутке. образует с осью
образует с осью  острый угол
острый угол  , то функция возрастает в этом промежутке. Если касательная к графику образует с осью
, то функция возрастает в этом промежутке. Если касательная к графику образует с осью  , функция убывает.
, функция убывает. возрастает в любом интервале, так как её производная
возрастает в любом интервале, так как её производная  всё время положительна, кроме точки
всё время положительна, кроме точки  , где она обращается в нуль.
, где она обращается в нуль. из области определения функции
из области определения функции  называется точкой максимума (минимума) этой функции, если существует такая δ - окрестность точки
называется точкой максимума (минимума) этой функции, если существует такая δ - окрестность точки  , что для всех
, что для всех  из этой окрестности выполняется неравенство
из этой окрестности выполняется неравенство 
 .
. или
или  не существует.
не существует.
 для всех
для всех  из
из  , а
, а 
 для всех
для всех  , то в точке
, то в точке  во всей δ-окрестности точки
во всей δ-окрестности точки 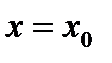 является точкой экстремума функции, если первая не обращающаяся в нуль производная в этой точке имеет четный порядок. При этом, если эта производная отрицательна (положительна), то критическая точка
является точкой экстремума функции, если первая не обращающаяся в нуль производная в этой точке имеет четный порядок. При этом, если эта производная отрицательна (положительна), то критическая точка  и
и  , тогда:
, тогда: , то
, то  , то
, то  .
. . Используя необходимое условие экстремума, получаем уравнение для нахождения критических точек:
. Используя необходимое условие экстремума, получаем уравнение для нахождения критических точек:  .
. , (*)
, (*) ;
;
 .
.
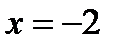 первая производная меняет знак с «+» на «-», следовательно, в точке
первая производная меняет знак с «+» на «-», следовательно, в точке 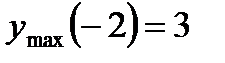 ; в точке
; в точке  первая производная меняет знак с «-» на «+», следовательно, в точке
первая производная меняет знак с «-» на «+», следовательно, в точке  . В точке
. В точке  .
. , т.е.
, т.е.  .
. .
.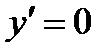 критические точки
критические точки  ,
, 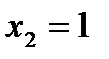 ,
,  не существует при
не существует при  , но эта точка не принадлежит области определения функции, следовательно, не может быть точкой экстремума.
, но эта точка не принадлежит области определения функции, следовательно, не может быть точкой экстремума. .
. , т.е. в точке
, т.е. в точке  данная функция имеет максимум,
данная функция имеет максимум,  ; в точке
; в точке  - минимум,
- минимум,  .
. называется выпуклым (вогнутым) на интервале
называется выпуклым (вогнутым) на интервале  , если он расположен ниже (выше) касательной, проведенной в любой точке кривой, соответствующей этому интервалу (рис.1).
, если он расположен ниже (выше) касательной, проведенной в любой точке кривой, соответствующей этому интервалу (рис.1).



 на интервале
на интервале  графика функции
графика функции 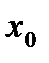 - абсцисса точки перегиба графика функции
- абсцисса точки перегиба графика функции  имеет разные знаки слева и справа от точки
имеет разные знаки слева и справа от точки  является вертикальной асимптотой кривой
является вертикальной асимптотой кривой  или
или 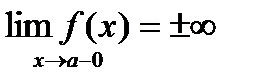 .
. является наклонной асимптотой кривой
является наклонной асимптотой кривой  ,
, 
 ,
,  .
. и
и  является горизонтальная асимптота. Существование горизонтальной асимптоты выявляется проще, чем существование наклонной асимптоты. Дадим специальное правило нахождения асимптоты в этом случае.
является горизонтальная асимптота. Существование горизонтальной асимптоты выявляется проще, чем существование наклонной асимптоты. Дадим специальное правило нахождения асимптоты в этом случае. является горизонтальной асимптотой кривой
является горизонтальной асимптотой кривой  или
или 

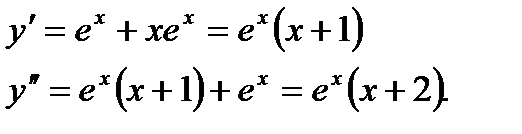
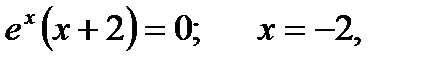 так как
так как  для любых
для любых  .
. на вспомогательном рисунке и исследовав знак второй производной в её окрестности, получаем слева от точки
на вспомогательном рисунке и исследовав знак второй производной в её окрестности, получаем слева от точки  (кривая выпуклая), а справа -
(кривая выпуклая), а справа -  (кривая вогнутая). Таким образом, при переходе через точку
(кривая вогнутая). Таким образом, при переходе через точку  вторая производная меняет знак, следовательно точка с абсциссой
вторая производная меняет знак, следовательно точка с абсциссой  .
.
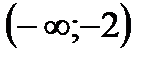 кривая выпуклая, а на интервале
кривая выпуклая, а на интервале  - вогнутая,
- вогнутая, 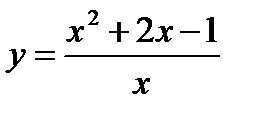 .
. .
.

 , т.е. ось
, т.е. ось  есть вертикальная асимптота (и слева, и справа).
есть вертикальная асимптота (и слева, и справа).
 т.е.
т.е. 

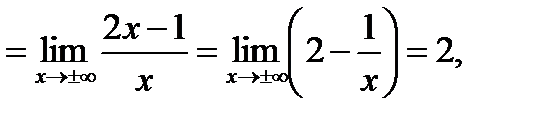
 .
. есть наклонная асимптота и влево, и вправо данной кривой (рис. 3).
есть наклонная асимптота и влево, и вправо данной кривой (рис. 3).



