
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства бесконечно малых и бесконечно больших последовательностей.
1) Пусть 2) Пусть 3) Если 4) Если Последовательность В частности, постоянная последовательность Можно доказать, что сходящаяся последовательность является ограниченной. Следовательно, к постоянной или сходящейся последовательности Свойства можно использовать для вычисления пределов, причем свойства 3) и 4) распространяются на любое конечное число слагаемых и множителей. Примеры. Найти пределы: 1) 2) 3) Действия с пределами. Даны Теорема. Если Эту теорему можно сформулировать по-другому: Теорема. Если существует Теорема применяется при вычислении пределов, при этом дополнительно могут использоваться и свойства бесконечно малых и бесконечно больших. Примеры. Найти пределы 1)
2)
3)
Неопределенности. Теорема о действиях с пределами справедлива лишь в случае, если
Обобщенная теорема. 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) Рассмотрим конкретные примеры. 1)
Можно взять конкретные k: k=3, k=0, k=5. 2)
3)
4)
Таким образом, складывая Обобщенная теорема позволяет расширить границы решаемых примеров, но не дает ответа в случаях неопределенностей Примеры. Найти пределы: 1) Такой способ решения называется делением числителя и знаменателя на 2)
Такой способ называется умножением числителя и знаменателя на выражение, сопряженное числителю или знаменателю. 3)
Этот способ называется сокращением на общий множитель (здесь Напомним, что Предел функции. Основные определения и понятия. Пусть функция Число Другими словами, число
Рисунок дает геометрическую иллюстрацию определения.
Число Иначе говоря, число Рисунок дает геометрическую иллюстрацию определения.
Если Прямая Основные теоремы о пределах функций. 1. 2. 3. Функция Функция Если
График имеет один из следующих четырех вариантов
|
||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 262; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.112.69 (0.048 с.) |
 бесконечно малая и при всех
бесконечно малая и при всех 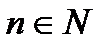
 . Тогда
. Тогда  является бесконечно большой.
является бесконечно большой. бесконечно большая и
бесконечно большая и 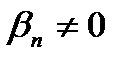 при всех
при всех  является бесконечно малой.
является бесконечно малой. ,
,  являются бесконечно малыми.
являются бесконечно малыми. является бесконечно малой.
является бесконечно малой. называется ограниченной, если существует число
называется ограниченной, если существует число  такое, что при всех
такое, что при всех  .
. , где
, где  - число, является ограниченной.
- число, является ограниченной. .
. , так как
, так как  ,
,  и
и  являются бесконечно малыми и их сумма тоже.
являются бесконечно малыми и их сумма тоже. , так как
, так как  - ограниченная и
- ограниченная и  или по-другому
или по-другому  - ограниченная,
- ограниченная,  - бесконечно малая
- бесконечно малая  бесконечно малая. Далее
бесконечно малая. Далее  бесконечно малая.
бесконечно малая. - две последовательности. Их суммой (разностью) называется последовательность
- две последовательности. Их суммой (разностью) называется последовательность 
 ; их произведением называется последовательность
; их произведением называется последовательность  ; их частным называется последовательность
; их частным называется последовательность  , если
, если  при всех
при всех  .
. и
и  , то
, то  ,
, 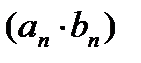 и
и  при
при  ;
;  и
и  , если
, если 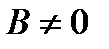 .
. и
и  ,
,  ;
;  и
и 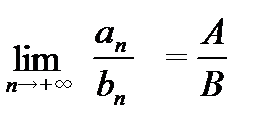 , если
, если 





 и
и  являются числами. Можно доказать обобщенную теорему о действиях с пределами, в которой возможны равенства
являются числами. Можно доказать обобщенную теорему о действиях с пределами, в которой возможны равенства  ,
, 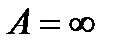 ,
,  ,
,  и
и 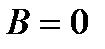 в случае частного
в случае частного  ,
,  , то
, то  . Из этой строгой записи оставим только символическую запись:
. Из этой строгой записи оставим только символическую запись:  . Далее всю теорему запишем символически.
. Далее всю теорему запишем символически.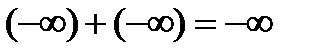
 ,
,  - число
- число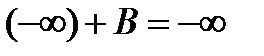 ,
,  - число
- число - неопределенность
- неопределенность
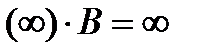 , если
, если 
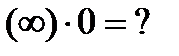 - неопределенность
- неопределенность ,
,  - число
- число ,
,  ,
, 
 - неопределенность
- неопределенность - неопределенность
- неопределенность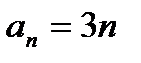 ,
,  , k – любое число.
, k – любое число. ,
, 
 .
. ,
, 
 ,
, 

 ,
, 
 ,
, 


 ,
, 
 не существует, так как последовательность
не существует, так как последовательность  или подробнее -1, +1, -1, +1, -1, +1,... не может стремиться ни к какому числу.
или подробнее -1, +1, -1, +1, -1, +1,... не может стремиться ни к какому числу. и
и  можем получить любое число k, можем получить также
можем получить любое число k, можем получить также 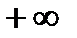 ,
,  , можем получить отсутствие предела. Это и считается неопределенностью, в отличие, скажем, от пункта 6), где при любых конкретных
, можем получить отсутствие предела. Это и считается неопределенностью, в отличие, скажем, от пункта 6), где при любых конкретных  и
и  обязательно получится, что
обязательно получится, что  .
. ,
,  ,
,  и
и  , так как в этих случаях ответа в общем виде нельзя дать – ответ зависит от конкретных последовательностей. Нахождение предела в случае неопределенности называется раскрытием неопределенности. Существует ряд приемов раскрытия неопределенностей, которые рассмотрим на примерах.
, так как в этих случаях ответа в общем виде нельзя дать – ответ зависит от конкретных последовательностей. Нахождение предела в случае неопределенности называется раскрытием неопределенности. Существует ряд приемов раскрытия неопределенностей, которые рассмотрим на примерах.
 в высшей степени (здесь
в высшей степени (здесь  ) для неопределенности
) для неопределенности 



 ) числителя и знаменателя. Кроме того, использовали деление на высшую степень.
) числителя и знаменателя. Кроме того, использовали деление на высшую степень.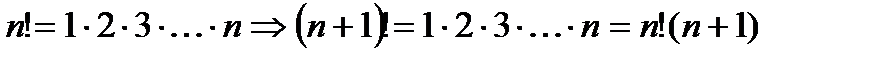
 определена в некоторой окрестности точки
определена в некоторой окрестности точки 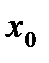 , быть может, за исключением самой точки
, быть может, за исключением самой точки 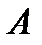 называется пределом функции
называется пределом функции 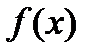 при
при  стремящемся к числу
стремящемся к числу  (пишут
(пишут 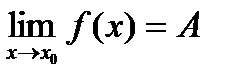 ), если для любого
), если для любого  существует
существует  , что для всех
, что для всех  , имеет место неравенство
, имеет место неравенство  .
.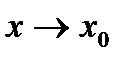 , если для всех значений
, если для всех значений  , достаточно мало отличающихся от числа
, достаточно мало отличающихся от числа  , в которых функция определена).
, в которых функция определена).
 (пишут
(пишут  ), если для любого
), если для любого  , что для всех
, что для всех  , имеет место неравенство
, имеет место неравенство 
 .
.

 .
. называется бесконечно малой при
называется бесконечно малой при 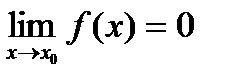 .
. ), если для любого числа
), если для любого числа 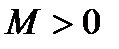 существует такое число
существует такое число  , имеет место неравенство
, имеет место неравенство  .
. , то график функции
, то график функции  . Прямая
. Прямая 


