
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Последовательность и ее предел.Содержание книги
Поиск на нашем сайте
Числовой последовательностью называется числовая функция Примеры последовательностей. 1) 2)
Короткая запись этой последовательности 3) Для последовательности можно рассматривать понятие монотонности (как частного случая монотонной функции), но нельзя рассматривать четность и периодичность, так как Числовая последовательность Геометрически последовательность можно изобразить двумя способами: 1) как функцию графиком на плоскости и 2) точками на прямой.
 получим получим
Данная последовательность Заметим, что при увеличении номера Число Смысл предела Обозначают предел следующим образом:
Пример. Покажем по определению, что
Смысл состоит в том, что при
Смысл состоит в том, что
Смысл состоит в том, что Примеры. 1) 2) 3) Последовательность Заметим, что Примеры. 1) 2) Последовательность Последовательность Заметим, что из условий Примеры. 1) 2) 3)
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 197; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.23.98.40 (0.007 с.) |

 , заданная на множестве натуральных чисел. Будем называть числовую последовательность просто последовательность. Обозначают ее так:
, заданная на множестве натуральных чисел. Будем называть числовую последовательность просто последовательность. Обозначают ее так:  ,
, 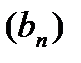 ,
,  ,
,  ,
,  и т.д. Индекс
и т.д. Индекс  указывает на значение аргумента,
указывает на значение аргумента, 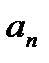 - значение функции (
- значение функции (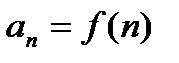 ).
). .
.  .
.  - члены последовательности;
- члены последовательности;  -
-  член последовательности.
член последовательности. .
. 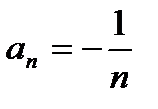 . Подробная запись этой последовательности выглядит так:
. Подробная запись этой последовательности выглядит так: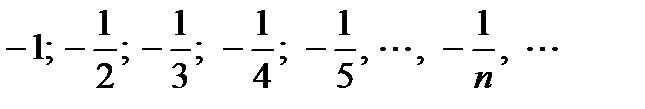
 ,
,  .
.
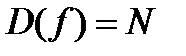 .
. называется невозрастающей (неубывающей), если для любого номера п справедливо неравенство
называется невозрастающей (неубывающей), если для любого номера п справедливо неравенство  . Если
. Если  , то последовательность
, то последовательность 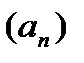 - убывающая (возрастающая). Невозрастающие и неубывающие последовательности называются монотонными.
- убывающая (возрастающая). Невозрастающие и неубывающие последовательности называются монотонными.
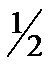

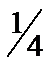

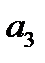





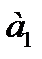
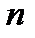 член последовательности
член последовательности 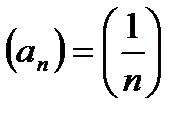 приближается к числу 0, то есть расстояние от
приближается к числу 0, то есть расстояние от  до 0 становится меньше любого задуманного положительного числа
до 0 становится меньше любого задуманного положительного числа  . Таким образом, при
. Таким образом, при  , член последовательности
, член последовательности  называется пределом последовательности
называется пределом последовательности 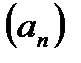 , если для любого
, если для любого  существует число
существует число  , что для всех натуральных чисел
, что для всех натуральных чисел 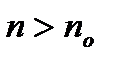 выполняется неравенство
выполняется неравенство 


 , члены последовательности
, члены последовательности 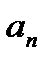 близки к
близки к 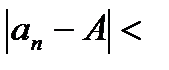
 - любое число и, следовательно,
- любое число и, следовательно,  или
или  при
при 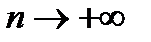 .
.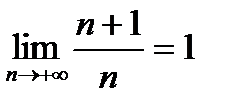 . Берем любое
. Берем любое 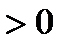 . Рассмотрим неравенство
. Рассмотрим неравенство 

 . В качестве
. В качестве  возьмем
возьмем  . (Если взять
. (Если взять  - целая часть
- целая часть  , то
, то  существует
существует  такое, что из
такое, что из  , что означает
, что означает  .
. , если для любого
, если для любого  существует
существует  такое, что для всех натуральных
такое, что для всех натуральных  .
.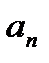 становится больше любого как угодно большого положительного числа
становится больше любого как угодно большого положительного числа  .
. , если для любого
, если для любого 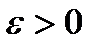 существует
существует 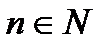 из
из  .
.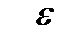 при достаточно больших номерах
при достаточно больших номерах  , если для любого числа
, если для любого числа  существует число
существует число  .
.

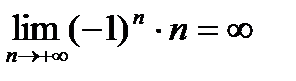
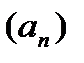 называется сходящейся, если она имеет конечный предел
называется сходящейся, если она имеет конечный предел  . Тогда говорят, что
. Тогда говорят, что  при
при  . В противном случае
. В противном случае 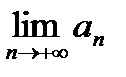 не существует совсем.
не существует совсем. не имеет предела
не имеет предела не имеет предела, так как
не имеет предела, так как 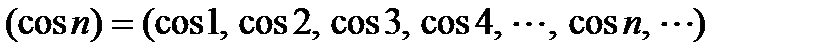 не может стремиться ни к какому числу (в силу периодичности
не может стремиться ни к какому числу (в силу периодичности 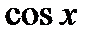 ), и в силу ограниченности, не может стремиться к
), и в силу ограниченности, не может стремиться к 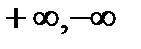 или
или  .
. называется бесконечно малой (б/м), если
называется бесконечно малой (б/м), если  или, если для любого
или, если для любого  существует
существует  .
. называется бесконечно большой (б/б), если
называется бесконечно большой (б/б), если  или для любого
или для любого  существует
существует  что для всех
что для всех  из
из 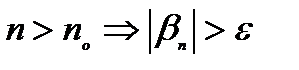 .
.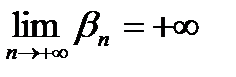 или
или 
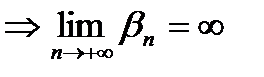 и
и 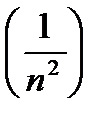 является бесконечно малой
является бесконечно малой является бесконечно большой
является бесконечно большой является бесконечно большой, так как
является бесконечно большой, так как  при
при  .
.


