
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раздел 2. Элементы линейной алгебрыСтр 1 из 8Следующая ⇒
Матрицы. Основные определения. Совокупность Матрицы принято обозначать прописными буквами А,В, С,… одним из следующих способов:
Коротко обозначают так: где
Матрица, имеющая лишь один столбец, называется вектор-столбцом
Матрица, все элементы которой равны нулю, называется нулевой матрицей и обозначается
Матрица, состоящая из одного числа, отождествляется с этим числом, т.е. любое число можно рассмотреть как матрицу размерности Квадратной матрицей называется матрица, у которой число строк равно числу столбцов
В противном случае матрица называется прямоугольной. Порядком квадратной матрицы называется число ее строк (или столбцов). Главной диагональю квадратной матрицы (2) называется диагональ, идущая из левого верхнего угла в правый нижний. На главной диагонали стоят элементы Побочной диагональю квадратной матрицы называется диагональ, идущая из левого нижнего угла в правый верхний. На ней стоят элементы Квадратная матрица, у которой отличны от нуля лишь элементы главной диагонали, называется диагональной. Если все элементы диагональной матрицы равны единице, то такая матрица называется единичной и обозначается
Треугольной матрицей называется квадратная матрица, все элементы которой, расположенные по одну сторону от главной диагонали, равны нулю. Различают соответственно верхнюю и нижнюю треугольные матрицы:
Ненулевая матрица называется ступенчатой, если выполняются следующие условия: а) первая строка матрицы имеет хотя бы один ненулевой элемент; б) первый ненулевой элемент любой последующей строки матрицы располагается правее первого ненулевого элемента предыдущей строки;
в) любая строка, состоящая только из нулей, находится ниже всех ненулевых строк. Две матрицы А=(аij) и В=(bij) одной размерности называется равными, если для любых i,j выполняются условие: аij=bij. Операции над матрицами Умножение матрицы на число. Произведением матрицы А на число a называется матрица
Например, Произведение матрицы А на число 0 есть нулевая матрица, т.е. Сложение матриц. Суммой двух матриц А и В одинакового размера называется матрица С=А+В, элементы которой определяются равенством Например,
Линейные операции над матрицами обладают следующими свойствами: 1) А+В=В+А- коммутативность; 2) (А+В)+С=А+(В+С)- ассоциативность; 3) А+ 0 =А; 4) А+(-А)= 0; 5) a(A+B)=aА+aВ-дистрибутивность относительно матриц; 6) (a+β)A=aA+βA- дистрибутивность относительно чисел; 7) (aβ)А=a(βА) Эти свойства справедливы для любых матриц А, В и С одинакового размера и любых a и β. Произведение матриц. Даны матрица А размером
Произведением матрицы А на матрицу В называется матрица
Отсюда видно, что умножать матрицу А на матрицу В можно только тогда, когда число столбцов матрицы А равно числу строк матрицы В. При этом матрица С=А·В будет иметь размер Пример. Пусть Произведение А·В здесь существует, так как
Произведение В·А этих же матриц не определено, т.к. число столбцов матрицы В не равно числу строк матрицы А. Уже из приведенного примера следует, что произведение матриц не коммутативно, т.е. А·В¹В·А в общем случае. Однако, даже если произведения А·В и В·А существуют, равенство А·В=В·А может не выполняться.
Справедливы следующие свойства: 1. (А·В)·С=А·(В·С) 2. А·(В+С)=А·В+А·С 3. (А+В)·С=А·С+В·С 4. a(А·В)=(aА)·В=А·(aВ) Предполагается, что матрицы А, В и С здесь имеют нужные размеры. Транспонирование матриц. Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется матрицей, транспонированной относительно данной. Матрицу, транспонированную относительно матрицы А, обозначим через Ат. Таким образом, если
Отметим, что если А матрица размером 1. 2. 3. 4.
Определители. Любой квадратной матрице А можно поставить в соответствие число, вычисляемое по определенному правилу и называемое определителем или детерминантом матрицы. В зависимости от порядка матрицы и определители называют соответственно определителями второго порядка, третьего порядка и т. д. Обозначают определители символами |А|, det А или
Последняя запись является определителем n-го порядка, отвечающим матрице
|
||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 293; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.246.254 (0.009 с.) |
 чисел (действительных или комплексных), расположенных в виде таблицы, содержащей
чисел (действительных или комплексных), расположенных в виде таблицы, содержащей  строк и
строк и  столбцов, называют матрицей размерности
столбцов, называют матрицей размерности  . Числа, составляющие матрицу, называются элементами матрицы.
. Числа, составляющие матрицу, называются элементами матрицы. (1)
(1) ,
, - элемент матрицы, индексы i,j определяют положение элемента в матрице. Первый индекс i определяет номер строки, второй j - номер столбца. Матрица, состоящая из одной строки, называется вектор-строкой. Такая матрица имеет вид:
- элемент матрицы, индексы i,j определяют положение элемента в матрице. Первый индекс i определяет номер строки, второй j - номер столбца. Матрица, состоящая из одной строки, называется вектор-строкой. Такая матрица имеет вид:
 .
. .
. , т.е. имеющую одну строку и один столбец.
, т.е. имеющую одну строку и один столбец. , т. е. матрица вида
, т. е. матрица вида (2)
(2) , т.е. элементы, у которых номер строки равен номеру столбца
, т.е. элементы, у которых номер строки равен номеру столбца  .
.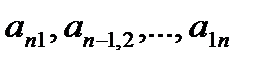 .
. .
.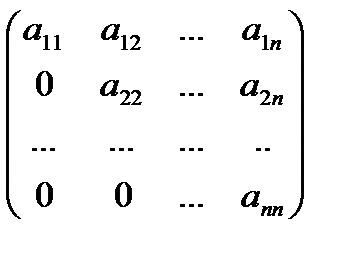 ,
, 
 , получаемая из А умножением всех ее элементов на число a:
, получаемая из А умножением всех ее элементов на число a: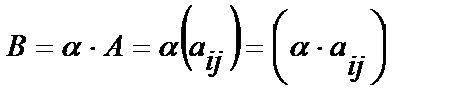

 .
. . Матрица А не изменяется при умножении на единицу. Матрица (-1)А называется противоположной матрице А и обозначается –А.
. Матрица А не изменяется при умножении на единицу. Матрица (-1)А называется противоположной матрице А и обозначается –А.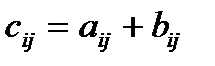
 (т.е. матрицы складываются поэлементно).
(т.е. матрицы складываются поэлементно).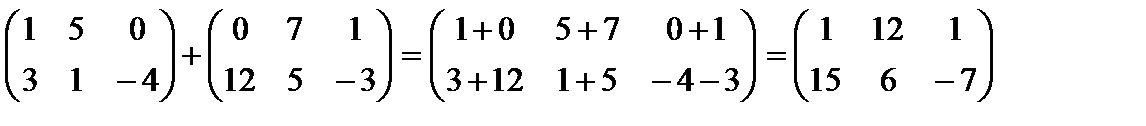
 и матрица В размером
и матрица В размером 
 ,
,  .
. , каждый элемент с ij которой равен произведению i -ой строки матрицы А на j -ый столбец матрицы В. Умножение строки на столбец производится по формуле:
, каждый элемент с ij которой равен произведению i -ой строки матрицы А на j -ый столбец матрицы В. Умножение строки на столбец производится по формуле:

 , т.е. число строк m в ней равно числу строк первой матрицы в составе произведения А·В, а число столбцов n - числу столбцов второй матрицы. Это соотношение
, т.е. число строк m в ней равно числу строк первой матрицы в составе произведения А·В, а число столбцов n - числу столбцов второй матрицы. Это соотношение  называют правилом размерностей.
называют правилом размерностей. ,
,  .
. , т.е. матрица А·В имеет размер
, т.е. матрица А·В имеет размер  .
.
 .
. , то
, то 
 , то матрица Ат имеет размеры
, то матрица Ат имеет размеры  . Операция нахождения матрицы, транспонированной к данной, называется транспонированием матрицы. Справедливы следующие свойства:
. Операция нахождения матрицы, транспонированной к данной, называется транспонированием матрицы. Справедливы следующие свойства:


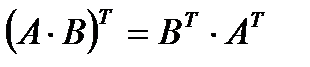
 .
.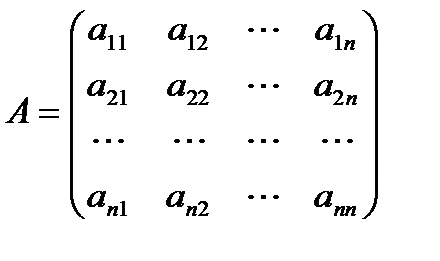 .
.


