
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Матричный метод решения СЛАУ.
Систему Пусть дана система уравнений (3), основная матрица А которой невырожденная. Система имеет единственное решение, которое можно найти по формуле:
где Пример. Решить систему предыдущего пункта матричным методом. Решение. Данная система в матричной форме имеет вид 1) Находим обратную матрицу 1. 2.
3. 4. 5. 2) Ответ: Метод Гаусса. Полный ответ на вопрос о существовании решения системы Для того чтобы система уравнений (1) была совместна, необходимо и достаточно, чтобы ранг расширенной матрицы был равен рангу основной матрицы системы. Если ранги основной и расширенной матриц совпадают с числом неизвестных, то система имеет единственное решение. Если ранг В последнем случае Метод Гаусса (метод последовательного исключения неизвестных). Метод Гаусса состоит в том, что при помощи элементарных преобразований систему приводят к такому виду, чтобы ее расширенная матрица оказалась трапециевидной (ступенчатой). После этого уже не представляет труда разобраться в вопросе о совместности системы, определить число решений и найти сами решения. Пример. Решить систему Решение. Выписываем расширенную матрицу системы. С помощью элементарных преобразований приведем матрицу к ступенчатому виду
Если не учитывать последний столбец, найдем ранг основной матрицы
Далее порядок действий очевиден. Из последнего уравнения
Замечания. При переходе от первой матрицы ко второй в качестве рабочей строки бралась первая, которая умножалась соответственно на 2 и (-1) и складывалась со второй и третьей строками. В результате мы получили нули в первом столбце. При переходе от второй матрицы к третьей в качестве рабочей строки бралась вторая, которая умножалась на (-2) и складывалась с третьей строкой. Пример. Исследовать систему Решение. Составим расширенную матрицу и приведем ее к ступенчатому виду.
Так как Пример. Решить систему Решение. Так как
Базисными неизвестными являются
где
|
|||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 436; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.33.178 (0.007 с.) |
 линейных алгебраических уравнений с
линейных алгебраических уравнений с  ,
, - матрица, обратная к А.
- матрица, обратная к А. , где
, где  ,
,  ,
,  . Ее решение
. Ее решение  .
.
 ,
, ,
, ,
, ,
,  ,
,  ,
, ,
, 





 ,
,  ,
, 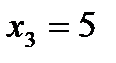 .
. линейных уравнений с
линейных уравнений с  основной и расширенной матриц меньше числа неизвестных
основной и расширенной матриц меньше числа неизвестных  , то система (1) имеет бесконечное множество решений.
, то система (1) имеет бесконечное множество решений. - свободными. Свободным неизвестным можно придавать произвольные значения, тогда оставшиеся
- свободными. Свободным неизвестным можно придавать произвольные значения, тогда оставшиеся  .
.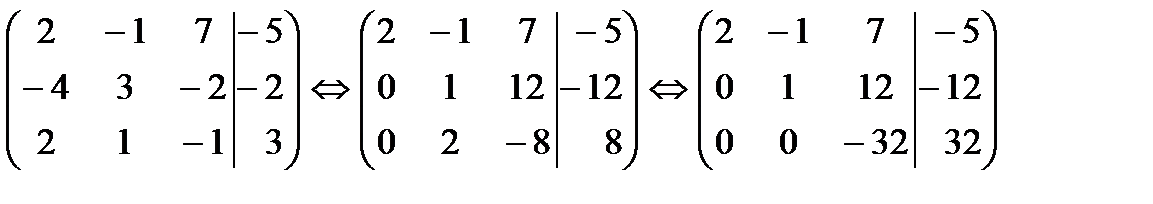
 ; учитывая последней столбец, найдем ранг расширенной матрицы
; учитывая последней столбец, найдем ранг расширенной матрицы  . Число неизвестных тоже равно 3. Система совместна и имеет единственное решение. Полученной матрице соответствует эквивалентная система:
. Число неизвестных тоже равно 3. Система совместна и имеет единственное решение. Полученной матрице соответствует эквивалентная система:
 ; подставляя это значение во второе уравнение, мы получаем
; подставляя это значение во второе уравнение, мы получаем  . И наконец, из первого уравнения находим
. И наконец, из первого уравнения находим  .
. .
.
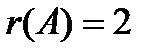 ,
,  .
.
 , то система совместна. Она имеет бесчисленное множество решений, потому что ранг матрицы меньше числа неизвестных. Восстановим систему по последней матрице:
, то система совместна. Она имеет бесчисленное множество решений, потому что ранг матрицы меньше числа неизвестных. Восстановим систему по последней матрице:
 и
и  , переменная
, переменная  - свободной. Обратной подстановкой найдем
- свободной. Обратной подстановкой найдем  ,
,


