Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие моделирования как процесса. Понятие модели. Основные свойства модели. Адекватность модели. Три основных иерархических уровня моделирования (математического описания).Стр 1 из 7Следующая ⇒
Понятие моделирования как процесса. Понятие модели. Основные свойства модели. Адекватность модели. Три основных иерархических уровня моделирования (математического описания). Тех. объект – тех. система – машина, механизм, тех. комплекс, технологический процесс, а также любой их компонент, выделяемый в процессе декомпозиции. Процесс моделирования – процесс, состоящий в выявлении осн св-в исследуемого объекта, построение моделей и их применении для прогнозирования поведения исследуемого объекта. Модель – физ./матем. констр-я, определ. образом отображ. объект и служащая для его изучения. Св-ва моделей: 1. модель отображает те св-ва объекта, кот. важны для его изучения в данном исполнении; 2. модель всегда проще объекта; 3. модель д.б. адекватна объекту, она должна верно отображать интересующие нас св-ва и соотв-но давать реальные прогнозы поведения. В завис-ти от уровня абстраг-ния при описании тех.сист различают 3 иерарх. уровня модел-вания: 1) микро-уровень; 2) макро-уровень; 3) мета-уровень. Микро-уровень. Исп-ся мат модели, описыв. процессы в сплошных средах. Для форм-ния этих мат моделей, кот. представляют собой ур-я в частных производных, исп-ся методы матем. физики. Примеры: диф. ур-я для эл-динамики, теплопроводности, теории упругости газ. динамики. Макро-уровень. Производится дискретизация производства с выделением эл-тов в качестве отдельных деталей. При этом из числа переменных искл-ся пространств. коорд-ты. Модели на макро-уровне предст-ся обыкнов. диф. ур-ми. Фазовые переменные: токи, напряжения, моменты, скорости угл. и лин. Мета-уровень. Производится дальнейшее абстрагирование от особенностей протекания физ. процессов и строятся модели информац. процессов. Мат. модели представляются в виде обыкновенных диф. ур-ий. логико-динамических сист, имитационных моделей. Аналитическое моделирование. Методы исследования аналитических моделей. Для аналит. мод-ния характерно то, что процессы функц-ия элементов системы зап-ся в виде некоторых функцион. соотношений (алгебр., интегро-диф., конечно-разностных и т.д.) или лог. условий. Методы исследования аналит.моделей: аналитический (стремятся получить в общем виде явные завис-ти для искомых характ-к; численный ( не умея решать ур-я в общем виде, стремятся получить числ. результаты при конкр. нач. данных; качественный (не имея решения в явном виде, можно найти некоторые св-ва решения (ex: оценить устойчивость).
Наиболее полное исслед-е процесса функц-ния можно получить, если известны явные зав-ти, связ. искомые характ-ки с нач. усл., параметрами и переменными исслед. системы, т.е. в результате аналит. решения задачи. Однако такие завис-ти удается получить только для простых систем. Численный метод позволяет иссл-ть, более широкий класс систем, но получ. решения носят частный характер. При иссл-нии сложных систем наиболее эффект. явл-ся методы имитац. мод-ния.
Автоматизированное моделирование 1ым этапом сл-ет считать создание библ-к числен. методов исслед-ния с-м. В совр. с-мах автоматизированного модел-ния исп-ся графические ср-ва задания исходной инф-ции о модели. п-са числен. расчетов – п-па Data Flow, или п-па потока данных. Можно отметить след. факторы, способствующие внедрению с-м автоматизированного модел-ния: ·трудоемкость получения математической модели сложных технических объектов, связанная с опасностью совершить ошибку в многочисленных преобразованиях модельных выражений; ·необходимость многовариантного моделирования, при котором необходимо иметь для одного объекта несколько моделей, отличающихся по сложности; ·желание иметь дружественный интерфейс с программой и возможность оперативно вносить изменения в модель, что проще всего на основе использования графических языков задания исходной информации. Варианты Data Flow и Control Flow управления процессом структурного моделирования Структурное модел-ние предусматривает 2 варианта управления п-сом моделирования: · поток команд (Control Flow), · поток данных (Data Flow). П-п потока команд – это обычный п-п записи программ в текстовых языках программирования, где инструкции вып-ся в той послед-ти, в к-ой они написаны. Если в п-се выполнения очередной инструкции программа обнаруживает, что какие-то данные не определены, это рассматривается как ошибка и влечет за собой остановку программы. Жесткие формы языков программирования, на основе к-ых формируется моделирующая программа при использ-нии п-па Control Flow, плохо сочетаются с возрастающим уровнем граф, языков. При любой форме задания графической инф-ции ее необходимо преобразовать в выполняемые инструкции, т.е. послед-ть команд для процессора, т.к. код граф, языка не может выполняться "строка за строкой". Это ведет к необходимости автоматически преобразовывать введенные пользователем или построенные графическим интерфейсом уравнения к формам, с которыми могут работать, например, библиотеки программных реализаций численных методов.
В этом случае эффективной явл-ся технология потока данных (Dataflow). САМ, работающая на поточной технологии управления процессом моделирования, обязательно содержит блок, упорядочивающий поток данных (информационный поток). Технология потока данных – с-ма программирования, состоящая из исполняемых узлов данных. Узлы выполняются только тогда, когда все необходимые данные поступят на их входы. 14. Классификации методов численного интегрирования: · методы явные и неявные; · методы одношаговые и многошаговые; · методы первого, второго и т.д. порядков; · методы с постоянным шагом и методы с автоматическим выбором шага Методы явные и неявные
Более точное значение интеграла дает метод трапеций, к-му соответствует отрезок 3. Тогда Для явных процедура форм-ния модели для числ. интег-ния огранич-ся алгебр-цией исх. диф.ур-й. Для неявн. методов дальнейшие д-вия зав-ят от того, какой метод решения с-мы нелин. ур-ий реализован в данном пакете. Этап подготовки мат. моделей для неявн. методов, к-ый состоит в линеаризации нелин. алгебраических ур-ий, т.е. в разложении нелин. ф-ий в р.Тэйлора Пусть задано нелинейное алгебраическое уравнение Разложение в ряд Тэйлора:
Т.о., п-с числен. модел-ния в общ. случае нелин. с-м неявн. методами состоит в форм-нии и решении на каждом шаге интег-ния с-мы лин. алгебр. ур-ий: Подготовка ДУ к численному интегрированию Реальные мехатронные объекты и мехатронные системы описываются, как правило, системами нелинейных алгебраических и дифференциальных уравнений. Для большинства задач, представляющих практический интерес, решение их аналитическими методами невозможно. Результаты могут быть получены путем построения приближенных решений с помощью численных методов интегрирования, в частности конечно-разностных методов. Общая идея численного интегрирования обыкновенного дифференциального уравнения (ОДУ)
где Процедура интегрирования предполагает решение полученной системы конечно-разностных уравнений для фиксированных моментов времени
Метод графов связи Метод графов связей относится к группе топологических методов, т.е. методов, использующих графическое представление исследуемого объекта. Он позволяет на единой методологической базе моделировать объекты, содержащие элементы различной физической природы – электрические, механические, электро-механические, гидравлические, пневматические и т.д. Метод графов связей является удобным инструментом для теоретического получения моделей систем небольшой сложности. Это связано с высокой степенью формализации метода, в частности введением моделей узлов, что позволяет оперировать только компонентными уравнениями при формировании моделей сложных объектов. Основные определения графов связей Метод графов связей (ГС) основан на представлении о том, что любые физ. процессы состоят из элементарных актов преобразования энергии. Метод ГС демонстрирует единство природы и протекающих в ней физ. процессов. Граф связей – совокупность элементов, соответствующих основным типам преобразования энергии и изображаемых в качестве вершин графа, соединенных связями. Для каждой связи в графе определены 6 величин, 3 из которых являются интегральными. Каждый элемент графа хар-ся ур-ем или с-мой ур-ий отн-но переменных относящихся к его связям. Переменные связей Основными переменными связей являются усилие
Мощность и момент Причинность в графе связей
Требования причинности: 1) Причинность связи с источником опр-ся типом источника, и каждый имеет один вариант причинности. 2) Аккумуляторы имеют 2 типа причинности: интегр-ую и диф-ную. 3) Гиратор и трансформатор имеет 2 варианта расстановки причинности: прямое и обратное включение. 4) 0- узел может иметь только 1 причинную по отн-нию к узлу связь. 5) 1-узел имеет все причинности связи и одну непричинную. Рекомендации расстановки причинности: 1) расставляются причинности на источниках 2) задаются связи на аккумуляторах исходя из каких-то соображений 3) послед-но в соот-вии с правилами расставляются причинности на всех остальных эл-тах 4) если есть причинные противоречия то придется изменить причинность на аккумуляторе. Варианты расстановки символов причинности на ГС
22.Эквивалентные преобразования графов связей Одним из достоинств ГС явл-ся возм-ть эквивалентных преобраз-ний, позволяющих упростить граф.
Понятие моделирования как процесса. Понятие модели. Основные свойства модели. Адекватность модели. Три основных иерархических уровня моделирования (математического описания). Тех. объект – тех. система – машина, механизм, тех. комплекс, технологический процесс, а также любой их компонент, выделяемый в процессе декомпозиции. Процесс моделирования – процесс, состоящий в выявлении осн св-в исследуемого объекта, построение моделей и их применении для прогнозирования поведения исследуемого объекта. Модель – физ./матем. констр-я, определ. образом отображ. объект и служащая для его изучения. Св-ва моделей: 1. модель отображает те св-ва объекта, кот. важны для его изучения в данном исполнении; 2. модель всегда проще объекта; 3. модель д.б. адекватна объекту, она должна верно отображать интересующие нас св-ва и соотв-но давать реальные прогнозы поведения. В завис-ти от уровня абстраг-ния при описании тех.сист различают 3 иерарх. уровня модел-вания: 1) микро-уровень; 2) макро-уровень; 3) мета-уровень. Микро-уровень. Исп-ся мат модели, описыв. процессы в сплошных средах. Для форм-ния этих мат моделей, кот. представляют собой ур-я в частных производных, исп-ся методы матем. физики. Примеры: диф. ур-я для эл-динамики, теплопроводности, теории упругости газ. динамики. Макро-уровень. Производится дискретизация производства с выделением эл-тов в качестве отдельных деталей. При этом из числа переменных искл-ся пространств. коорд-ты. Модели на макро-уровне предст-ся обыкнов. диф. ур-ми. Фазовые переменные: токи, напряжения, моменты, скорости угл. и лин.
Мета-уровень. Производится дальнейшее абстрагирование от особенностей протекания физ. процессов и строятся модели информац. процессов. Мат. модели представляются в виде обыкновенных диф. ур-ий. логико-динамических сист, имитационных моделей.
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 125; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.38.125 (0.035 с.) |
 Если задано диф. ур-е
Если задано диф. ур-е 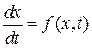 (3.1) и начальные условия
(3.1) и начальные условия  , то очередное значение
, то очередное значение 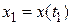 :
:  Опр. интеграл численно = площади под кривой
Опр. интеграл численно = площади под кривой  на интервале
на интервале  . Приближенно эта площадь м.б. вычислена как площадь прямоуг-ка, высота к-го = зн-нию ф-ции
. Приближенно эта площадь м.б. вычислена как площадь прямоуг-ка, высота к-го = зн-нию ф-ции  на левой границе интервала или зн-нию
на левой границе интервала или зн-нию  на правой границе.
на правой границе.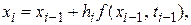 (3,3) явн метод. Неизвестное значение
(3,3) явн метод. Неизвестное значение  м.б. непосредственно вычислено по известному значению
м.б. непосредственно вычислено по известному значению 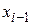 в предыдущей точке.
в предыдущей точке. . не явн метод. Здесь в правой части выражения исп-ся неизвестное зн-ие
. не явн метод. Здесь в правой части выражения исп-ся неизвестное зн-ие 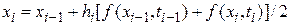 .
. где
где  - вектор переменных.
- вектор переменных. где
где  –нач. приближение, в кач-ве к-го берутся зн-ния переменных на предыд. шаге интег-ния;
–нач. приближение, в кач-ве к-го берутся зн-ния переменных на предыд. шаге интег-ния; 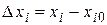 ;
;  – неизв. зн-ние переменной на шаге интег-ния. м.б. записано как лин.алг. ур-ие:
– неизв. зн-ние переменной на шаге интег-ния. м.б. записано как лин.алг. ур-ие: , где
, где  ,
, 
 к-ая вкл-ет компонентн. и топологич. ур-ния моделируемой схемы.
к-ая вкл-ет компонентн. и топологич. ур-ния моделируемой схемы.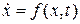 заключается в том, что производится дискретизация независимой переменной - времени
заключается в том, что производится дискретизация независимой переменной - времени  на интервале
на интервале  и замена ее рядом значений
и замена ее рядом значений  (принцип
(принцип  ). Расстояние между двумя соседними значениями
). Расстояние между двумя соседними значениями  называется шагом интегрирования. В частном случае он может быть постоянным на всем заданном интервале изменения переменной
называется шагом интегрирования. В частном случае он может быть постоянным на всем заданном интервале изменения переменной 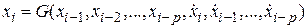 ,
, – некоторая вектор-функция, определяемая способом построения метода;
– некоторая вектор-функция, определяемая способом построения метода; 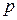 – количество предыдущих точек, которые используются в методе интегрирования.
– количество предыдущих точек, которые используются в методе интегрирования. , начиная с момента
, начиная с момента  , для которого определено начальное состояние исследуемой системы
, для которого определено начальное состояние исследуемой системы  . Соответственно, решение получается в виде совокупности значений
. Соответственно, решение получается в виде совокупности значений  для заданных моментов времени.
для заданных моментов времени. и поток
и поток  . Эти величины являются функциями времени и называются переменными мощности связи. Остальные четыре переменные вычисляются через основные по формулам:
. Эти величины являются функциями времени и называются переменными мощности связи. Остальные четыре переменные вычисляются через основные по формулам: энергия
энергия  , перемещение
, перемещение 
 Величина
Величина  – полезная энергия, передаваемая через связь в направлении, определенном полустрелкой.
– полезная энергия, передаваемая через связь в направлении, определенном полустрелкой. Причинность задается причинной стрелкой – отрезком на одном из концов связиВ 1ом варианте поток
Причинность задается причинной стрелкой – отрезком на одном из концов связиВ 1ом варианте поток  явл-ся причиной, а усилие
явл-ся причиной, а усилие 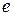 явл-ся следствием (ур-ние:
явл-ся следствием (ур-ние: 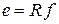 ). 2вар. соот-ет ур-ие:
). 2вар. соот-ет ур-ие:  . Здесь причиной для эл-та
. Здесь причиной для эл-та  явл-ся усилие
явл-ся усилие 
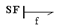























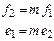









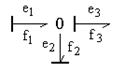





 .
.