
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Выбор между явными и неявными методами в процедурах моделирования мехатронных с-м (их достоинства и недостатки)
Неявные методы лучше приспособлены для решения систем диф. и алгебраических уравнений, к тому же они более устойчивы. В рез-те, несмотря на большие затраты машинного времени на каждом шаге интегрирования, связанные с необходимостью решения с-м лин. алгебраических ур-ний, общ. затраты м.б. знач-но меньше за счет увеличения шага интегрирования и уменьшения общего кол-ва шагов. Рассмотрим эту особенность.
Применим указанные формулы для численного интегрирования простейшего лин. ДУ:
Характеристическое уравнение данной динамической системы имеет вид Разностное ур-ие, соответствующее численному решению явным методом Эйлера, запишется как
Условие уст-ти полученного ур-ия: Для метода Рунге-Кутты 4-го порядка требование устойчивости ограничивает шаг величиной Применение неявного метода Эйлера к той же системе дает
где ограничение на величину шага выглядит по другому: Подготовка ДУ к численному интегрированию Реальные мехатронные объекты и мехатронные системы описываются, как правило, системами нелинейных алгебраических и дифференциальных уравнений. Для большинства задач, представляющих практический интерес, решение их аналитическими методами невозможно. Результаты могут быть получены путем построения приближенных решений с помощью численных методов интегрирования, в частности конечно-разностных методов. Общая идея численного интегрирования обыкновенного дифференциального уравнения (ОДУ)
где
Процедура интегрирования предполагает решение полученной системы конечно-разностных уравнений для фиксированных моментов времени
|
|||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 160; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.189.177 (0.005 с.) |
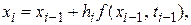
 .
.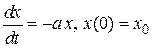 .
.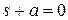 , или
, или  , где
, где 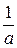 – постоянная времени системы.
– постоянная времени системы. .
.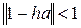 или
или  ..
.. , или, в более общем виде,
, или, в более общем виде,  , где
, где 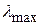 – макс. Собств. значение матрицы Якоби.
– макс. Собств. значение матрицы Якоби. ,
,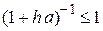 , что позволяет выбрать шаг любой величины, ориентируясь только на требуемый уровень погрешности.
, что позволяет выбрать шаг любой величины, ориентируясь только на требуемый уровень погрешности.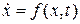 заключается в том, что производится дискретизация независимой переменной - времени
заключается в том, что производится дискретизация независимой переменной - времени  на интервале
на интервале  и замена ее рядом значений
и замена ее рядом значений  (принцип
(принцип  ). Расстояние между двумя соседними значениями
). Расстояние между двумя соседними значениями  называется шагом интегрирования. В частном случае он может быть постоянным на всем заданном интервале изменения переменной
называется шагом интегрирования. В частном случае он может быть постоянным на всем заданном интервале изменения переменной 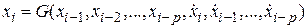 ,
, – некоторая вектор-функция, определяемая способом построения метода;
– некоторая вектор-функция, определяемая способом построения метода; 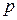 – количество предыдущих точек, которые используются в методе интегрирования.
– количество предыдущих точек, которые используются в методе интегрирования. , начиная с момента
, начиная с момента  , для которого определено начальное состояние исследуемой системы
, для которого определено начальное состояние исследуемой системы  . Соответственно, решение получается в виде совокупности значений
. Соответственно, решение получается в виде совокупности значений  для заданных моментов времени.
для заданных моментов времени.


