
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Графический интерфейс программ математического моделирования динамических систем
Дает возм-ть оперировать с графическими образами вместо аналитических выражений. позволяет вводить информацию об исследуемой системе путем "рисования" на экране проектируемой схемы. Формой графического представления информации о моделируемой системе м. являться: · операторно-структурные схемы, принятые в ТАУ; · функциональные и принципиальные схемы различных физических устройств; · кинематические схемы механизмов; · сигнальные графы; · графы связей; · блок–схемы алгоритмов и другие графические модели. Задачами графического интерфейса, кроме того, могут быть: · контроль за соблюдением некот. правил в п-се создания граф. Изобр-ния на экране монитора; · преобразование инф-ции о схеме в команды для моделирующей программы; · контроль за процессом моделирования, визуализация рез-тов моделирования и др.
Иерархическое моделирование (проектирование). Иерархическое проектирование является типовым при разработке сложных технических объектов и заключается в разбиении исходной задачи на подзадачи. Составные части - уровни проектирования. В один уровень, как правило, включаются представления, имеющие общую физическую основу и допускающие для своего описания использование одного и того же математического аппарата. Уровни проектирования можно выделять по степени подробности, с какой отражаются свойства проектируемого объекта. В результате такого подхода объект проектирования декомпозируется на фрагменты (подсхемы) и проектирование каждого из них ведется в определенном смысле самостоятельно. На каждом уровне иерархии этот принцип применяется вновь, что позволяет заменить решение одной сложной задачи многократным решением задач меньшей размерности. Использование принципа иерархического проектирования позволяет ограничить текущую сложность проекта на приемлемом уровне. Иерархическое проектирование может осуществляться сверху вниз (для новых объектов) и снизу вверх (обычно при модернизации объектов).
Структурное и мультидоменное физическое моделирование Структурным моделированием наз-тся техника моделирования, основанная на использовании моделей в виде блоков, для которых определены входы и выходы. Соответственно, блоки рассматриваются как преобразователи входных сигналов в выходные. При моделировании лин. с-м связи между входными и выходными сигналами устанавливаются посредством задания передаточных функций. Для нелинейных систем эти связи задаются нелинейными алгебраическими или д. у. Поскольку структурные блоки имеют выраженные входы и выходы, построенные согласно этой технике модели иногда наз-ют направленными сигнальными графами.
Физическим мультидоменным моделированием называется техника моделирования, основанная на использовании библиотеки моделей элементов физических устройств, из которых можно составлять схемы физические принципиальные. Поскольку в энергетических цепях поток энергии может менять направление, то для элементов физических схем входы и выходы не определены. Частным случаем данной техники моделирования является использование графов связей. Идеология физического мультидоменного моделирования заключается в том, что модель любого технического устройства строится как преобразующая энергию цепь. В распоряжении пользователя предоставляется библиотека элементов физических устройств
Варианты Data Flow и Control Flow управления процессом структурного моделирования Структурное модел-ние предусматривает 2 варианта управления п-сом моделирования: · поток команд (Control Flow), · поток данных (Data Flow). П-п потока команд – это обычный п-п записи программ в текстовых языках программирования, где инструкции вып-ся в той послед-ти, в к-ой они написаны. Если в п-се выполнения очередной инструкции программа обнаруживает, что какие-то данные не определены, это рассматривается как ошибка и влечет за собой остановку программы. Жесткие формы языков программирования, на основе к-ых формируется моделирующая программа при использ-нии п-па Control Flow, плохо сочетаются с возрастающим уровнем граф, языков. При любой форме задания графической инф-ции ее необходимо преобразовать в выполняемые инструкции, т.е. послед-ть команд для процессора, т.к. код граф, языка не может выполняться "строка за строкой". Это ведет к необходимости автоматически преобразовывать введенные пользователем или построенные графическим интерфейсом уравнения к формам, с которыми могут работать, например, библиотеки программных реализаций численных методов.
В этом случае эффективной явл-ся технология потока данных (Dataflow). САМ, работающая на поточной технологии управления процессом моделирования, обязательно содержит блок, упорядочивающий поток данных (информационный поток). Технология потока данных – с-ма программирования, состоящая из исполняемых узлов данных. Узлы выполняются только тогда, когда все необходимые данные поступят на их входы. 14. Классификации методов численного интегрирования: · методы явные и неявные; · методы одношаговые и многошаговые; · методы первого, второго и т.д. порядков; · методы с постоянным шагом и методы с автоматическим выбором шага Методы явные и неявные
Более точное значение интеграла дает метод трапеций, к-му соответствует отрезок 3. Тогда Для явных процедура форм-ния модели для числ. интег-ния огранич-ся алгебр-цией исх. диф.ур-й. Для неявн. методов дальнейшие д-вия зав-ят от того, какой метод решения с-мы нелин. ур-ий реализован в данном пакете. Этап подготовки мат. моделей для неявн. методов, к-ый состоит в линеаризации нелин. алгебраических ур-ий, т.е. в разложении нелин. ф-ий в р.Тэйлора Пусть задано нелинейное алгебраическое уравнение Разложение в ряд Тэйлора:
Т.о., п-с числен. модел-ния в общ. случае нелин. с-м неявн. методами состоит в форм-нии и решении на каждом шаге интег-ния с-мы лин. алгебр. ур-ий:
|
||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 109; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.41.214 (0.008 с.) |
 Если задано диф. ур-е
Если задано диф. ур-е 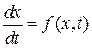 (3.1) и начальные условия
(3.1) и начальные условия  , то очередное значение
, то очередное значение 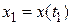 :
:  Опр. интеграл численно = площади под кривой
Опр. интеграл численно = площади под кривой  на интервале
на интервале  . Приближенно эта площадь м.б. вычислена как площадь прямоуг-ка, высота к-го = зн-нию ф-ции
. Приближенно эта площадь м.б. вычислена как площадь прямоуг-ка, высота к-го = зн-нию ф-ции  на левой границе интервала или зн-нию
на левой границе интервала или зн-нию  на правой границе.
на правой границе.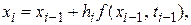 (3,3) явн метод. Неизвестное значение
(3,3) явн метод. Неизвестное значение  м.б. непосредственно вычислено по известному значению
м.б. непосредственно вычислено по известному значению 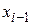 в предыдущей точке.
в предыдущей точке. . не явн метод. Здесь в правой части выражения исп-ся неизвестное зн-ие
. не явн метод. Здесь в правой части выражения исп-ся неизвестное зн-ие 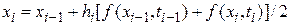 .
. где
где  - вектор переменных.
- вектор переменных. где
где  –нач. приближение, в кач-ве к-го берутся зн-ния переменных на предыд. шаге интег-ния;
–нач. приближение, в кач-ве к-го берутся зн-ния переменных на предыд. шаге интег-ния; 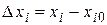 ;
;  – неизв. зн-ние переменной на шаге интег-ния. м.б. записано как лин.алг. ур-ие:
– неизв. зн-ние переменной на шаге интег-ния. м.б. записано как лин.алг. ур-ие: , где
, где  ,
, 
 к-ая вкл-ет компонентн. и топологич. ур-ния моделируемой схемы.
к-ая вкл-ет компонентн. и топологич. ур-ния моделируемой схемы.


