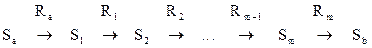Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод статистических испытаний (метод Монте – Карло)
К сожалению, построение аналитической модели по одной из рассмотренных выше схем удается далеко не всегда. Такая ситуация встречается при рассмотрении весьма сложных объектов или при рассмотрении новых систем, сведений о которых недостаточно для построения аналитической модели. В подобных случаях на помощь приходят так называемые численные методы. Численный метод решения математических задач при помощи моделирования случайных величин называется методом статистических испытаний или методом Монте-Карло. В основе метода лежит следующий факт: если имеется механизм генерирования (розыгрыша) значений равновероятно распределенной на отрезке [0,1] случайной величины, то легко получить случайные значения другой случайной величины, распределенной по любому заданному закону. Генерирование значений равновероятно распределенной случайной величины обычно осуществляется с помощью так называемых псевдослучайных чисел. Сегодня практически в каждом алгоритмическом языке или пакете прикладных программ имеется стандартная процедура генерирования случайных чисел. В программе достаточно написать
Генерация значений непрерывной случайной величины. Поставим задачу получить значения При заданном законе распределения вероятность попадания случайной величины
Это выражение можно рассматривать в качестве уравнения относительно неизвестной Функция распределения случайной величины X
Предположим, что случайная величина
Сравнивая это выражение с (1.3), получим
Соотношение (11) показывает, что величина 1. Генерируется 2. Записывается уравнение
3. Решается уравнение (12) относительно искомой величины
Пример 1. Розыгрыш равномерного распределения. Пусть задано распределение
Составляем уравнение
Отсюда легко получить искомый результат
Пример 2. Для случайной величины, распределенной по экспоненциальному закону
Таким образом, чтобы разыграть случайную величину, распределенную по экспоненциальному закону, необходимо разыграть значение равновероятно распределенной на отрезке [0,1] величины Для более сложных распределений не удается аналитически решить уравнение типа (12). Поэтому используют таблицы функций распределений. Так же разыгрывают равномерно распределенную величину
Генерация значений дискретной случайной величины. Пусть заданы значения вероятностей для некоторой дискретной случайной величины Идея решения данной задачи основана на попадании случайной точки на один из интервалов, каждый из которых пропорционален величине соответствующей вероятности Вначале, как всегда в методе Монте-Карло, генерируется
Логика этого правила заключается в следующем. Случайная точка
Замечание. В целом ряде задач практики встает вопрос о случайном выборе одной из заданного множества альтернатив, каждый из которых имеет определенный вес. Его решить можно по аналогии с описанным выше методом, положив в (14) вместо вероятности нормированную величину соответствующего веса (метод рондомизированного розыгрыша).
Решение. В соответствии с (14) имеем: k=1 - "13/34 = 0.382 > 0.73?" - нет; k=2 - "20/34 = 0.588 > 0.73?" - нет; k=3 - "31/34 = 0.912 > 0.73?" - да! Таким образом, выбрана третья альтернатива. Если бы выпало h = 0,59, то был бы выбран тот же вариант, а вот если h = 0,27, то первый и т.д.
Рассмотрим пример применения метода статистических испытаний. Пусть в данный прямоугольник вписана некоторая сложная фигура (см. рис.3.7.). Требуется определить площадь вписанной фигуры. Решение этой задачи при помощи метода статистических испытаний может происходить по следующей схеме. Реализуется механизм попадания в прямоугольник: разыгрываются случайные значения двух равновероятно распределенных случайных чисел из интервала
Формальную оценку числа розыгрышей можно получить на основании следующих рассуждений. Пусть требуется вычислить неизвестную величину
или в более компактной форме
Данное соотношение говорит о том, что среднее значение сгенерированной случайной величины с очень высокой вероятностью равно
Имитационное моделирование
В тех случаях, когда удовлетворительной аналитической модели построить не удается, делают попытку сформировать логико-аналитический комплекс, позволяющий с учетом внешних воздействий воспроизводить (имитировать) процесс функционирования системы. Наиболее характерным является следующая схема построения такого моделирующего комплекса. Рассматривается совокупность моделей элементов и их функциональные взаимосвязи, каждая из которых отображает соответствующий компонент объекта моделирования. Чаше всего модель элемента – это набор правил (алгоритмов) поведения по отношению к входным воздействиям и соответствующей логики изменения состояний элементов. В простейшем случае элемент может находиться в одном из двух состояний: в работоспособном или неработоспособном. В более сложных случаях в качестве элементов могут выступать более сложные модели.
Пусть вначале все составляющие моделирующего комплекса находится в каком-то известном исходном состоянии. Моделируется некоторое воздействие (внешнее или внутреннее), в результате которого в соответствии с заложенными правилами запускается процесс функционирования системы: элементы и их связи могут менять свое состояние, вызывая соответствующую реакцию других компонентов. Тем самым система в целом переходит в другое состояние (реализован один шаг). По некоторому правилу вырабатывается новое воздействие, но поскольку система находится в состоянии некотором отличном от исходного, то процесс функционирования может идти по иной траектории. Затем все повторяется. Такой циклический процесс (пошаговая имитация функционирования) продолжается до достижения системой поставленной цели, израсходования некоторого ресурса или иного условия остановки процесса. В результате может быть получена траектория движения системы в фазовом пространстве ее состояний, которая является объектом последующего изучения. Такого рода модели получили название имитационные модели, а проводимые на их основе исследования – имитационное моделирование По-существу, реализуется математический эксперимент в виде воспроизведения некоего аналога поведения рассматриваемого объекта. Как и в любом эксперименте над искусственным объектом здесь могут изменяться воздействия, правила реагирования на них, структура элементов и их связи. При формировании имитационных моделей наблюдается широкий спектр технологий. Наиболее простой и самый распространенный заключается в имитации процесса, базирующегося исключительно на методе стохастических испытаний, поэтому соответствующие модели правильное было бы называть стохастическими моделями. Как это реализуется? Те параметры, которые рассматриваются, как неопределенные, заменяются случайными величинами, законы распределения которых считаются известными. На каждом шаге производится розыгрыш возможных значений этих случайных величин, которые подставляются в модель, которая становится полностью детерминированной, что и позволяет произвести нужные расчеты или вынести суждения, необходимые для изменения состояния системы. Затем вновь разыгрываются значения случайных величин, и процесс расчетов повторяется. Простота такого подхода в том, что логика функционирования модели фиксирована еще при построении модели, и различия в поведении обусловлены исключительно случайно возникшим состоянием компонентов модели. Например, объект описывается дифференциальным уравнением с неопределенным коэффициентом. Имитируется розыгрыш значения этого коэффициента, подстановка которого в уравнение позволяет его решить. Другой пример. Рассматривается технологическая линия, которая моделируется сетью взаимосвязанных агрегатов. Каждый из агрегатов исполняет свою функцию случайным образом (например, за случайное время, со случайным качеством, в случайном объеме и т.п.). Если разыгрывать соответствующие законы распределения, то можно получить однозначный вариант возможного поведения каждого агрегата, а, следовательно, и всего объекта рассмотрения в целом. Повторив процесс многократно, набирают необходимую статистику, что позволяет сделать вполне определенные заключения.
Принципиальную трудность при построении имитационных моделей представляет вопрос упорядочивания шагов моделирования. Поскольку все они могут быть взаимозависимы, то от того в какой последовательности они воспроизводятся, зависит результат функционирования системы, заблаговременно же рассмотреть все возможные комбинации, как правило, невозможно. В этой связи применяют различные схемы. Наиболее известны две из них: по особым состояниям и с шагом по времени. Моделирование по принципу наступления особых событий (состояний). В качестве таких событий могут быть выделены: · поступление заявки; · освобождение канала связи; · возникновение отказа; · окончание ресурса и т.п. Процесс имитации развивался в последовательности рассмотрения очереди наступления особых событий. Для этого должен быть построен циклический алгоритм моделирования, который может быть сведен к следующей последовательности действий: 1. Для данного состояния системы формируется множество возможных наступлений особых событий, как продолжения процесса ее функционирования; 2. Среди возможных выбирается то событие, которое может начать происходить ранее других (событие с минимальным временем); 3. В зависимости от типа выделенного события (самого раннего из возможных для данной ситуации) предпринимаются соответствующие действия по изменению состояния системы и цикл вновь повторяется. Иначе говоря, жестко выбирается «следующее» существенное событие и производится имитация соответствующего конкретного шага функционирования системы.
Моделирование с шагом по времени (по принципу Считается, что моделирующий алгоритм, основанный на применении Важно понимать, что после каждого реализованного шага состояние системы в принципе изменяется. При этом в связи с использованием процедур случайного выбора, заранее результат каждого шага имитации неизвестен. Следовательно, на каждом шаге возможные продолжения и их количество могут быть различными, поэтому в каждом имитационном эксперименте может быть получена различная траектория изменений состояния системы.
В целом же имитационное моделирование – более широкое понятие, чем стохастическое моделирование. Остановимся на методологических аспектах имитационного моделирования [82]. Математическая модель может быть моделью либо косвенного, либо прямого описания. Модели косвенного описания – это формальные конструкции аналитических соотношений. Язык такого описания ограничен лишь четырьмя элементами: неизвестное, параметр, математическая операция и ограничения. Все рассмотренные выше модели относятся к моделям косвенного описания. При использовании моделей косвенного описания всегда возникает задача разрешения математических соотношений относительно неизвестных и (или) параметров модели, что обычно влечет за собой серьезные вычислительные трудности. Для решения задач, основанных на использовании моделей этого типа, разработано большое количество аналитических и численных методов, используются также методы качественного анализа. К моделям косвенного описания применимы методы математического анализа, математического программирования, регрессионные методы и т.п. Именно поэтому обучение математическому моделированию обычно сводится к изучению математических методов, оставляя без пристального внимания собственно процедуры построения математической модели. В общем случае между объектом и его косвенным описанием отсутствует структурное подобие. Пусть, к примеру, при решении задачи планирования производственной программы некоторого производства построена модель линейного программирования
Анализируя эту модель, исследователь интерпретирует получаемые результаты в терминах постановки задачи. Однако если другой исследователь, не знающий предметного содержания исходной задачи, увидит эту модель линейного программирования, то у него не будет оснований утверждать, что речь идет о производственной программе и именно данного предприятия. Иначе говоря, модели косвенного описания теряют структурное подобие описываемым объектам. Главное достоинство косвенных моделей заключается в том, что они, как правило, описывают широкий круг объектов и с той или иной степенью адекватности применимы для их исследования. Для использования такого рода моделей разрабатываются эффективные математические методы, которые широко изучаются и в целом известны. Принципиально важным является относительная универсальность косвенных математических моделей, т.е. применимость к достаточно широкому кругу объектов моделирования. По мере усложнения объекта рассмотрения построение достаточно адекватной модели становится возможным лишь с помощью так называемых моделей прямого описания. Характерной особенностью этих моделей является их структурное подобие рассматриваемому объекту (каждому компоненту рассматриваемого объекта соответствует некоторая конструкция модели). Проблема использования моделей прямого описания заключается в том, что такую модель можно построить только в том случае, если объект является конструктивным, т.е. вопрос о его существовании непосредственно связан с доказательством возможности построения этого объекта. В основе процесса построения конструктивных объектов лежат следующие положения [83]: · задана совокупность исходных объектов, рассматриваемых в качестве элементарных; · заданы правила образования новых объектов из построенных ранее; · построения осуществляются в рамках заданных правил отдельными шагами относительно простым способом. В качестве примера конструктивных объектов могут быть названы слова в конечном алфавите, конечные графы и автоматы, некоторые специальные алгоритмы и т.п. В конечном счете, конструктивный объект может быть описан совокупностью натуральных чисел. Конструктивные объекты являются предметами рассмотрения конструктивной математики. Одно из центральных мест в этом сравнительно новом направлении математики занимает изучение соответствий, заданных при помощи алгоритмов. Так, например, понятие традиционной математики "функция" связывается с теми соответствиями, которые описаны посредством алгоритма, позволяющего эффективно построить значения функций по значениям ее аргументов. Главное преимущество конструктивного способа построения математики состоит в том, что при этом сравнительно просто выявить те данные, по которым может быть построено решение данной задачи. На основе вышеизложенного сформулируем следующее определение: имитационной называем модель прямого описания конструктивного объекта. Процесс построения имитационной модели и последующее ее использование назовем имитационным моделированием. Теперь становятся очевидными и все основные черты имитационного моделирования. 1. Имитационная модель обычно изображается в виде алгоритма над данным алфавитом. По этой причине они могут быть также названы алгоритмическими. Это означает, что в некотором алфавите задано общепринятое предписание, определяющее потенциально осуществимый процесс над конструктивными объектами достаточно общего вида. Существует несколько стандартных форм изображения алгоритма, например, нормальные алгоритмы А.А.Маркова, машины Тьюринга, операторные алгоритмы Ван Хао, которые являются различными уточнениями интуитивного понимания алгоритма. Очень часто имитационные модели изображаются в виде взаимосвязанной совокупности конечных автоматов, что и приводит некоторых авторов к отождествлению понятий автоматных и имитационных моделей. В то же время перспективность построения имитационных моделей на основе конечных, и в первую очередь вероятностных и нечетких, автоматов не вызывает сомнений и подтверждается целым рядом работ [84] [85]. 2. Имитационные модели обеспечивают явное представление топологии рассматриваемых объектов, что является следствием прямого описания последних. Процедура прямого описания объекта заключается в следующем. Вначале объект расчленяется на элементарные составляющие. Между этими составляющими устанавливаются несложные, подчас простейшие взаимосвязи, которые могут быть воспроизведены чисто механическим путем, т.е. конструктивно. Следует подчеркнуть, что в некоторых моделях элементами могут выступать весьма сложные объекты, которые на данном уровне агрегирования воспринимаются в качестве неделимых и рассматриваются с точки зрения "входа-выхода". Именно это обстоятельство позволяет для одного и того же объекта в зависимости от целей и возможностей исследователя строить имитационные модели с различной степенью детализации. Таким образом, модульность построения имитационных моделей вытекает из самой сути этих моделей и является их характерной чертой. Конструктивный характер имитационных моделей, по крайней мере теоретически, позволяет достичь любой степени детализации, а, следовательно, адекватности описания рассматриваемого объекта. Имитационные модели могут быть составлены с таким приближением к реальному объекту, с каким позволяет наше понимание проблемы и необходимость предварительных требований. Это обстоятельство позволяет разрабатывать модели нескольких модификаций, предназначенных для различных уровней управления, ситуаций и решаемых задач, изменяя лишь степень детализации в описании отдельных сторон объекта моделирования. Отметим также, что имитационные модели допускают использование практически того же языка, что и язык описания реального объекта. 3. Имитационная модель - это всегда модель какого-либо дискретного (дискретизированного) процесса. Очевидность этого тезиса также вытекает из конструктивного характера моделируемого объекта. Любая имитационная модель - это математическая структура <S|R>, где S - множество возможных состояний объекта; R- множество правил, определяющих возможность перехода объекта из одного состояния в другое. Это, в частности, означает, что объект, находящийся в состоянии Sa переводится, если это возможно, в состояние Sb в результате последовательного (поэтапного) перехода в так называемые промежуточные состояния
причем Формально это есть описание траектории движения объекта в виде алгоритмизированной схемы "состояние - переход - состояние", что позволило некоторым авторам принять это свойство имитационных моделей за их определение. Если моделируемый объект не является дискретным, то для построения имитационной модели его необходимо вначале представить в дискретном виде, что, конечно же, приводит к огрублению описания объекта. По очевидным соображениям не имеет смысла говорить об имитационных моделях для статических объектов. В этом случае множество правил возможных переходов пусто, а множество возможных состояний представлено одним элементом S0. 4. В имитационных моделях широко используется идея рандомизированного розыгрыша. Для каждого конкретно данного состояния объекта возможно указать, вообще говоря, несколько состояний, в каждое из которых объект может быть переведен за один шаг. Выбор "следующего" состояния зависит от различных факторов и может реализоваться несколькими способами, например, на основании жестких правил предпочтения, случайным образом либо путем принятия волевого решения индивидуумом. Исторически первым для выбора " следующего" состояния был использован метод статистических испытаний (Монте-Карло), который позволяет реализовывать процедуры вариантных расчетов и проводить эксперименты на математических моделях с помощью ЭВМ. Успехи этого подхода, связанные в первую очередь с резким расширением круга решаемых задач, и относительная простота его реализации способствовали распространению мнения об эквивалентности имитационного моделирования и метода статистических испытаний, что является неверным по существу. В имитационных моделях при выборе "следующих" состояний часто используется метод статистических испытаний. Однако (и в этом суть имитационного моделирования) прошлая информация, вводимая в стохастические модели извне, заменяется фактическими данными, генерируемыми в машинном эксперименте самой моделью. Реализация этой идеи с широким использованием приложений теории нечетких множеств позволила по-новому взглянуть на возможность решения целого ряда сложных задач управления, в том числе и задач, связанных с созданием моделей искусственного интеллекта. 5. Имитационные модели реализуются главным образом на мощных вычислительных машинах. Эта их особенность часто ведет к отождествлению понятия имитационного моделирования с машинными экспериментами на математических моделях. Необходимость же применения для реализации имитационных моделей вычислительной техники связана с многоактностью соответствующих алгоритмов. Именно это обстоятельство объясняет тот факт, что практическая реализация имитационного моделирования стала возможной после широкого распространения быстродействующих компьютеров. Следует подчеркнуть, что в имитационном моделировании используется так называемый структуризированный диалог, характерной чертой которого является непосредственное изменение параметров и структуры модели в ходе эксперимента. Реализация имитационных моделей на компьютере есть одна из эффективных форм машинной имитации как процесса управляемого эксперимента, проводимого на ЭВМ над любой моделью системы. 6. Имитационное моделирование - основной инструмент практической реализации системного анализа. Имитационное моделирование развивается под давлением практической потребности исследования сложных систем и благодаря появлению компьютеров с развитым интерфейсом, позволяющим по-новому организовать ввод, вывод и отображение информации, а также интерактивный режим работы. Известно, что решение сложных задач не может быть достигнуто простыми способами. В данном случае этот тезис находит свое отражение в том, что имитационные модели сложных объектов, в свою очередь, являются весьма сложными конструкциями. Как правило, это целые имитационные системы, которые включают одну или несколько базовых имитационных моделей, их модификации, информационную базу и специальный управляющий алгоритм, обеспечивающий эффективное и целенаправленное взаимодействие всех элементов системы. В имитационных системах предполагается введение диалога для оперативного анализа получаемых результатов (в том числе и промежуточных), ввода необходимых корректив для проведения дальнейших расчетов, а также для осуществления не формализованных в модели элементов рассматриваемых процессов. Обобщая вышеизложенное, можно сказать, что методология имитационного моделирования во всем спектре его возможных приложений на сегодняшний день не имеет альтернатив. Вместе с тем разработка имитационных моделей реальных систем и процессов - удел специалистов в данной прикладной области знаний, достаточно подготовленных в вопросах математики и информатики. Как сказал Н.Моисеев: за имитационными моделями будущее [86].
Конструктивно-имитационный метод моделирования. Опытный руководитель в конкретно заданной обстановке, как правило, принимает весьма эффективные актуальные именно на данный момент («на сегодня») решения, назовем их частными решениями. Попытка принять решение, отнесенное на некоторую временную перспективу, часто вызывает у руководителя затруднения и сопровождается просьбами уточнить ожидаемую на момент принятия решения ситуацию. Поэтому, например, инженеры по знаниям, довольно успешно могут формализовать процедуры принятия руководителем частных решений. Попытки же экстраполировать применение этих процедур на перспективу («завтра» поступать так же как и «сегодня») обычно не имеют успеха (эффективные в данной ситуации решения в другой обстановке становятся не рациональными, а иногда и недопустимыми). Данные соображения были положены основу разработки конструктивно-имитационный метод моделирования процессов разработки планов функционирования организационных систем. Центральная идея метода решения рассматриваемого рода задач заключается в том, чтобы обеспечить формирование очередного решения только в актуальной ситуации (только «сегодня»). Почему? Дело в том, что в каждой конкретной полностью определенной обстановке (каковой, например, является исходное состояние системы) конструируется полная совокупность актуальных на данный момент вариантов частных решений. Каким-то образом одно из них принимается как решение. Затем производится имитация процессов реализации этих решений. В результате система приходит в новое вполне определенное состояние, и процедура повторяется вновь. Именно поэтому метод назван нами конструктивно-имитационным методом (КИМ-методом) [87]. Рассмотрим методику КИМ-метода. Объектом моделирования является пространственно-временной управляемый процесс функционирования системы. Его основу составляет цикл: ситуация (состояние) - формирование полного множества потенциально возможных частных решений – выбор одного из них в качестве решения – исполнение решения – переход в новое (обусловленное этим решением) состояние. Перед тем как описать основные этапы реализации КИМ-метода отметим два важных момента. Плановый период целесообразно разбить на некоторые интервалы, которые назовем временными квантами. Размер последних зависит от специфики рассматриваемой системы, однако в рамках одного кванта времени относительно данного компонента не может быть принято два или более противоречащих друг другу частных решения: например, принять и отменить некоторое решение (в последующие же временные интервалы изменение ранее принятых частных решений в принципе возможно). Это условие не слишком обременительно (всегда можно сузить временной квант), но обеспечивает внутреннюю непротиворечивость процесса формирования решения задачи.
|
|||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 412; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.119.251 (0.073 с.) |
 :
:  и
и  случайной величины
случайной величины  , распределенной в отрезке
, распределенной в отрезке  с заданной плотностью
с заданной плотностью  .
. находится по известно формуле
находится по известно формуле (8)
(8)
 монотонно возрастает от 0 до 1. Следовательно, прямая
монотонно возрастает от 0 до 1. Следовательно, прямая  (см. рис.3.5) пересекает график
(см. рис.3.5) пересекает график  в одной единственной точке, абсциссу которой принимаем за
в одной единственной точке, абсциссу которой принимаем за  Выберем произвольный интервал
Выберем произвольный интервал  , содержащийся в
, содержащийся в  , любой точке
, любой точке  соответствует ордината кривой
соответствует ордината кривой  . Поэтому, если
. Поэтому, если  принадлежит интервалу
принадлежит интервалу  (9)
(9)
 (10)
(10)
 . (11)
. (11) =
=  для всех
для всех  .
.
 .
. для
для  , окончательная формула имеет следующий вид
, окончательная формула имеет следующий вид (13)
(13) .
. . Ставится задача случайным образом выбрать одно из возможных значений
. Ставится задача случайным образом выбрать одно из возможных значений  .
. (14)
(14) , для которого впервые выполнится условие в (14).
, для которого впервые выполнится условие в (14).
 Рассмотрим пример. Имеются четыре альтернативы
Рассмотрим пример. Имеются четыре альтернативы  с весами:
с весами:  ,
, 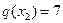 ,
,  и
и  . Какая альтернатива будет выбрана, если выпала
. Какая альтернатива будет выбрана, если выпала  h = 0,73?
h = 0,73? и
и  точек. Из них
точек. Из них  попадает во вписанную фигуру, а
попадает во вписанную фигуру, а  - вне ее
- вне ее  . За площадь фигуры
. За площадь фигуры  принимается отношение числа точек попавших в фигуру к общему числу разыгранных точек:
принимается отношение числа точек попавших в фигуру к общему числу разыгранных точек:  .
. Сколько розыгрышей (точек
Сколько розыгрышей (точек  ? Обычно поступают следующим образом. Производится серия из достаточно представительного числа точек (
? Обычно поступают следующим образом. Производится серия из достаточно представительного числа точек ( штук), в результате чего получается результат
штук), в результате чего получается результат  . Затем серия повторяется и если
. Затем серия повторяется и если ,
, то
то  принимается за конечный результат. В противном случае серии повторяются до тех пор, пока два последних результата не дадут отличие менее чем
принимается за конечный результат. В противном случае серии повторяются до тех пор, пока два последних результата не дадут отличие менее чем  . Предположим, что имеется такая случайная величина
. Предположим, что имеется такая случайная величина 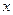 , что
, что  и
и  . Сгенерируем
. Сгенерируем  приближается к нормальному закону с параметрами: математическим ожиданием
приближается к нормальному закону с параметрами: математическим ожиданием 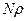 и дисперсией
и дисперсией  . Применяя правило "трех сигм", получаем приближенное равенство
. Применяя правило "трех сигм", получаем приближенное равенство
 (15)
(15)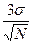 , стремящейся к нулю при возрастании
, стремящейся к нулю при возрастании  ). Суть этого подхода в движении по дискретизированному модельному времени. Для этого весь рассматриваемый период времени разбивается на относительно малые отрезки времени
). Суть этого подхода в движении по дискретизированному модельному времени. Для этого весь рассматриваемый период времени разбивается на относительно малые отрезки времени  и шагом является смещение границ рассматриваемого временного отрезка на
и шагом является смещение границ рассматриваемого временного отрезка на  ,
,  и т.д. Начиная с первого временного отрезка
и т.д. Начиная с первого временного отрезка  , пошагово реализуется цикл имитации всех событий, которые могут произойти в рамках этого временного отрезка при данном состоянии системы. В данной схеме допускается произвольная (в рамках заданной логики) последовательность рассматриваемых событий, которые происходят в границах данного временного интервала.
, пошагово реализуется цикл имитации всех событий, которые могут произойти в рамках этого временного отрезка при данном состоянии системы. В данной схеме допускается произвольная (в рамках заданной логики) последовательность рассматриваемых событий, которые происходят в границах данного временного интервала.