
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Типовые математические схемы
Функционирование разных по своей физической природе систем может описываться однотипными зависимостями. Это обстоятельство и положено в основу широкого распространения так называемых типовых схем математического моделирования. Рассмотрим широко известный пример. Пусть тело массой
где В самом простейшем случае, если пренебречь силой трения и внешней силой (колебания возникнут, если начальное отклонение тела от положения равновесия не равно нулю, т.е. принимаются некоторые начальные условия
которое называется уравнением свободных колебаний. Общий вид решения этого уравнения есть свободные колебания, описываемые функцией где Если рассматривать колебания математического маятника (тела подвешенного на невесомой нерастяжимой нити, длина l которой много больше размеров груза), получим уравнение, описывающее угол отклонения маятника от вертикального положения
Решение этого дает функция Рассмотрим теперь задачу об электромагнитных колебаниях в колебательном контуре, состоящем из идеального конденсатора емкости
решение которого также есть функция Возможность удовлетворительно описывать достаточно широкий спектр различных объектов, положена в основу построения соответствующих математических схем. Так уравнения второго порядка типа (6) описывают колебания практически любой одномерной идеальной системы. На практике же обычно принимаются в расчет и вводятся дополнительные силы и задаются начальными условиями. Тогда основу модели выступает уравнение типа (5), решение которого также является колебательный процесс, который может оказаться как затухающим, так расходящимся. Отметим, что этот факт является следствием второго закона Ньютона: для описания динамики простых физических систем типовой математической схемой является дифференциальное уравнение второго порядка (если рассматривается многомерный случай, то дифференциальное уравнение второго порядка в частных производных). Именно знания о тех или иных объектах природы и общества обычно лежат в основе типовых математических схем. Математические модели создаются в интересах многочисленных практических приложений на протяжении длительного периода развития науки. Часть из них, показав свою высокую эффективность для определенного спектра специфических групп объектов-оригиналов, хорошо отработана, зафиксирована в многочисленных учебных изданиях, находит широкое применение, и обычно называются типовыми математическими схемами. Для каждой из них описаны группы задач, где применения соответствующей схемы наиболее целесообразно. Исторически получилось так, что любая из этих схем берет свое начало от конкретной группы задач, за что и получила соответствующее имя. Ценность использования типовых математических схем обусловлена высоким уровнем разработанности соответствующих математических методов и инструментов их практического применения. Именно поэтому попытки построения математической модели (особенно при решении сложных задач) начинаются, как правило, с анализа возможности применения именно типовых схем. Эти схемы дают удовлетворительный результат при выполнении соответствующих требований к объекту исследования и в зависимости от условий конкретной задачи. В идеале каждая математическая схема требует жесткого выполнения вполне четких и характерных для нее требований. Исследуемые же объекты в целом не могут быть адекватными относительно этих требований, поэтому исследователь сам решает: можно ли в данном конкретном случае согласиться с требованиями применимости конкретной математической схемы или нет.Для этогополезно представлять суть отдельных требований, диктуемых каждой из типовых схем.
Как правило, к типовым математическим схемам относят: непрерывно-детерминированные; дискретно-детерминированные; дискретно-стохастические; непрерывно-стохастические, а также обобщенные (универсальные) модели. Как уже отмечалось, в основе каждой из типовых схем лежит определенная математическая модель, которая и дала такие их названия, как D-схема, F-схема и т.п. Из названий обычно следует и специфика этих схем. В основу классификации большинства традиционных математических схем положены две пары признаков моделируемого объекта: он принимается детерминированным или вероятностным и его функционирование описывается как непрерывное или дискретное. Так, детерминированные схемы, иногда их называют предсказуемыми, применяют для систем, относительно которых можно считать, что они функционируют по известным правилам и интересующий результат может быть заранее определен. Для моделирования систем, характеристики состояния и/или условия функционирования которых описываются случайными величинами, могут, вообще говоря, использоваться с тохастические схемы. Однако и это крайне важно подчеркнуть, стохастические схемы опираются на использование законов распределения вероятностей, а посему на результаты теории вероятностей. Главным же обстоятельством, которое определяет границы применимости теории вероятностей, является наличие у изучаемых явлений свойства статистической устойчивости, согласно которому рассматриваемые процессы при неизменных условиях носят массовый характер и описываемые их характеристики достаточно стабильны (сходятся). Еще в 1938 году А.Н. Колмогоров по этому поводу писал: «… обслуживание математиками прикладных нужд в области математической статистики и теории вероятностей имело до сих пор несколько случайный, любительский характер, направляясь, по большей части или личными связями или специальными интересами отдельных исследователей» [74]. К сожалению, этому «пороку» подвержены и некоторые современные исследователи. Обоснованность того или иного подхода в значительной мере зависит и от угла зрения на рассматриваемую систему, которую необходимо четко обозначать. Например, каждый студент, обучающийся в данном вузе по определенной программе, изучает известный набор учебных дисциплин, в установленные сроки сдает фиксированное количество экзаменов и т.д. Рассматриваемая здесь схема обучения вполне может быть считаться детерминированной. Если же рассматривать вопросы оценки успеваемости, то соответствующие процессы могут моделироваться, как стохастические. Кратко рассмотрим традиционные схемы моделирования, которые широко и подробно описаны в литературе.
|
||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 187; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.63.136 (0.005 с.) |
 , прикрепленное через пружину, может двигаться в горизонтальном направлении под действие некоторой внешней (сонаправленной с движением маятника) силы
, прикрепленное через пружину, может двигаться в горизонтальном направлении под действие некоторой внешней (сонаправленной с движением маятника) силы  . Состояние такого маятника можно описать одним параметром – расстоянием от положения равновесия. Введем соответствующее обозначение: в каждый момент времени
. Состояние такого маятника можно описать одним параметром – расстоянием от положения равновесия. Введем соответствующее обозначение: в каждый момент времени  тело находится на расстоянии
тело находится на расстоянии  . Будем предполагать, что тело совершает движения в соответствии со вторым законом Ньютона: сила инерции равна сумме всех действующих сил, а именно силы трения (которая пропорциональна скорости), силы упругости пружины (пропорциональной отклонению от положения равновесия) и внешней возбуждающей силы. В связи с вышеизложенным уравнение горизонтального пружинного маятника может быть записано в следующем виде
. Будем предполагать, что тело совершает движения в соответствии со вторым законом Ньютона: сила инерции равна сумме всех действующих сил, а именно силы трения (которая пропорциональна скорости), силы упругости пружины (пропорциональной отклонению от положения равновесия) и внешней возбуждающей силы. В связи с вышеизложенным уравнение горизонтального пружинного маятника может быть записано в следующем виде , (5)
, (5)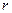 и
и  - соответствующие коэффициенты пропорциональности.
- соответствующие коэффициенты пропорциональности. ), то уравнение примет вид
), то уравнение примет вид , (6)
, (6) ,
, - циклическая частота колебаний,
- циклическая частота колебаний, 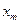 - амплитуда колебания,
- амплитуда колебания,  - начальная фаза.
- начальная фаза.

 , где часта колебаний
, где часта колебаний  .
. и катушки индуктивности с известной индуктивностью
и катушки индуктивности с известной индуктивностью  . Как известно еще из элементарного курса физики, уравнение описывающее динамику заряда на конденсаторе
. Как известно еще из элементарного курса физики, уравнение описывающее динамику заряда на конденсаторе  в так называемом
в так называемом  -контуре (при отсутствии активного сопротивления) имеет вид
-контуре (при отсутствии активного сопротивления) имеет вид ,
,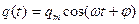 , где
, где  - частота колебаний.
- частота колебаний.


