
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Четность, нечетность и периодичность функцииСтр 1 из 5Следующая ⇒
ФУНКЦИИ И ИХ ГРАФИКИ Определение функции
Пусть каждому числу х из некоторого множества Х поставлено в соответствие определенное число у. Тогда говорят, что на множестве Х задана функция. Пишут: y = f (x).
Переменная х называется независимой переменной (аргументом), а переменная у зависимой. Множество Х называется областью определения данной функции и обозначается D (f), а множество всех чисел у, соответствующих различным числам х Если числу х 0 у 0 называется значением функции в точке х 0 (или при х = х 0). График функции
Пусть заданы прямоугольная система координат Оху и функция y = f (x). Графиком функции f (x) называется множество всех точек плоскости с координатами (х; f (x)), где х График функции y = f (x) зачастую можно построить с помощью преобразований (сдвиг, растяжение) графика некоторой уже известной функции. В частности: 1. График функции y = f (x) + а получается из графика функции y = f (x) сдвигом вдоль оси Оу на | a | единиц (вверх, если а > 0, и вниз, если а < 0). 2. График функции y = f (x – b) получается из графика функции y = f (x) сдвигом вдоль оси Оx на | b | единиц (вправо, если b > 0, и влево, если b < 0). 3. График функции y = k f (x) получается из графика функции y = f (x) растяжением вдоль оси Оу в k раз. 4. График функции y = f (mx) получается из графика функции y = f (x) сжатием по оси Ох в m раз. 5. График функции y = – f (x) получается из графика функции y = f (x) симметричным отражением относительно оси Ох. 6. График функции y = f (– x) получается из графика функции y = f (x) симметричным отражением относительно оси Оу.
Четность, нечетность и периодичность функции
Функция называется четной, если f (– x) = f (x). График четной функции симметричен относительно оси Оу.
Функция называется нечетной, если f (– x) = – f (x). График нечетной функции симметричен относительно начала координат. Функция, не являющаяся ни четной, ни нечетной, называется функцией общего вида (положения).
Функция f (x) называется периодической, если существует такое число Т > 0, что
1) х – T
Число Т называется периодом функции f (х). Если Т – период функции f (х), то числа
Гиперболические функции
Гиперболический тангенс: у = th x =
Для гиперболических функций имеют место формулы, аналогичные (с точностью до знака) соответствующим формулам для тригонометрических функций:
ch2 x – sh2 x = 1, ch2 x = ch2 x + sh2 x,
ch(x
ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ
Пределы и неравенства 1. Пусть все члены данной сходящейся последовательности неотрицательны. Тогда ее предел также неотрицателен. 2. Пусть каждый член одной сходящейся последовательности больше или равен соответствующему члену другой сходящейся последовательности. Тогда и предел первой последовательности больше или равен пределу второй последовательности 3. Теорема о промежуточной переменной (о двух милиционерах): Пусть соответствующие члены трех данных последовательностей { an }, { bn } и { сn } удовлетворяют условию an £ bn £ сn. Тогда если последовательности { an } и { сn } сходятся к одному и тому же пределу, то последовательность { bn } также сходится к этому пределу.
Определение предела
Окрестностью точки х 0 называется любой интервал с центром в точке х 0. Пусть функция f (x) определена в окрестности точки х 0 кроме, быть может, самой точки х 0.
Первое определение предела функции (Гейне): Число А называется пределом функции f (x) в точке х 0, если для любой последовательности { хn }, сходящейся к х 0 (хn ¹ х 0 " n), последовательность { f (xn)} соответствующих значений функции сходится к А. Обозначение: Второе определение предела функции (Коши) (эквивалентно первому):
Односторонние пределы Пусть функция f (x) определена в правой полуокрестности точки х 0, т.е. на некотором интервале (х 0, х 0 + d), где d > 0. Тогда говорят, что число А называется пределом функции f (x) справа в точке х 0 (или правосторонним пределом), если для любой последовательности { хn }, сходящейся к х 0 и такой, что все ее члены больше, чем х 0, соответствующая последовательность значений функции { f (xn)} сходится к числу А.
Обозначение: Аналогично определяется предел функции f (x) слева (или левосторонним предел) в точке х 0, обозначаемый
Замечательные пределы
Первый замечательный предел Второй замечательный предел
Вычисление пределов
Пределы с тригонометрией в большинстве случаев следует максимально упростить! НЕПРЕРЫВНОСТЬ ФУНКЦИИ Односторонняя непрерывность
Функция f (x) называется непрерывной слева в точке х 0, если она определена на некотором полуинтервале (a; x 0] и Функция f (x) называется непрерывной справа в точке х 0, если она определена на некотором полуинтервале [ x 0; b ] и Функция f (x) непрерывна в точке х 0 тогда и только тогда, когда она непрерывна слева и справа в этой точке, т.е.
Точки разрыва функции
Пусть точка х 0 принадлежит области определения функции f (x) или является граничной точкой этой области. Точка х 0 называется точкой разрыва функции f (x), если f (x) не является непрерывной в этой точке. Точки разрыва подразделяются на точки разрыва 1-го рода и 2-го рода.
собой, или же односторонние пределы равны между собой,
в бесконечность), то х 0 называется точкой разрыва 2-го рода. ПРОИЗВОДНАЯ Производная функции
Понятие производной Пусть функция у = f (x) определена в некоторой окрестности точки х 0. Предел отношения приращения D у функции в этой точке (если он существует) к приращению D х аргумента, когда D х ® 0, называется производной функции f (x) в точкех 0. Т.о.
f ′(х 0) = Вычисление производной называется дифференцированием функции.
Пример 1. Пользуясь определением, найти производные функций: у = f (x): a) y = 3 x 2, b) y = sin x.
a) Придадим аргументу х приращение Δ х. Тогда соответствующее приращение Δ у функции будет иметь вид: Δ у = f (x + Δ х) – f (x) = 3(x + Δ х)2 – 3 x 2 = 3(x 2 + 2 х Δ х + (Δ х)2 – x 2) = 3Δ х (2 х + Δ х) =>
b) Имеем Δ у = sin (x + Δ х) – sin (x) = 2sin
Таблица производных
Логарифмическая производная При нахождении производных от показательно-степенной функции u (x) v ( x ), а также других громоздких выражений, допускающих логарифмирование (произведение, частное и извлечение корня), удобно применять логарифмическую производную.
Логарифмической производной от функции у = f (x) называется производная от логарифма этой функции (ln y)′ =
Пример 4. Найти производную от функции у = хх. • Прологарифмируем обе части равенства у = хх: ln y = x ln x. Продифференцируем полученное равенство (у есть функция от х!): y′ = хх (ln x + 1).
Производная неявной функции Пусть функция у = у (x), обладающая производной в точке х, задана неявно уравнением F (x, y) = 0. (1)
Тогда производную у¢ (x) этой функции можно найти, продифференцировав уравнение (1) (при этом у считается функцией от х) и разрешая затем полученное уравнение относительно у¢. Пример 5. Найти производную неявно заданной функции у: х 3 + у 3 = sin (x – 2 y).
• Дифференцируя обе части уравнения и учитывая, что у – есть функция от х (поэтому, например, (у 3) ¢= 3 у 2 y ′), получим: 3 х 2 + 3 у 2 y ′ = cos (x – 2 y) ∙ (1 – 2 y ′) => y ′ (3 у 2 + 2cos (x – 2 y)) = cos (x – 2 y) – 3 х 2 => y ′ =
Производные высших порядков Производная f ¢(x) от функции f (x) называется также производной первого порядка. В свою очередь производная от функции f ¢ (x) называется производной второго порядка от функции f (x) (или второйпроизводной) и обозначается f¢¢ (x). Аналогично определяется производная третьего порядка (или третьяпроизводная), обозначаемая f¢¢¢ (x) и т.д. Производная n -ого порядка обозначается f ( n )(x). Для функции, заданной параметрически (x = x (t), y = у (t)), вторая производная у¢¢ (x) находится по формуле Пример 10. Найти: а) f ¢¢¢ (x), где f (x) = sin 3 x; b) y¢¢xx дляфункции у = у (х), заданной параметрически x = t 2, y = t 3.
· a) Находим первую производную f ¢(х) = (sin 3 x) ¢ = 3 cos 3 x. отсюда получаем вторую производную f ¢¢(х) = (3 cos 3 x) ¢ = – 9 sin 3 x, а затем искомую третью: f ¢¢¢(х) = (– 9 sin 3 x) ¢ = – 27 cos 3 x.
Задание для самостоятельного решения
Найти производные указанных порядков для следующих функций: a) y = tg 3 x, y ¢¢ =? b) y = – x cos x, y ¢¢ =? c) y = ln2 x, y ¢¢ =? d) y = x × ln x, y ¢¢¢ =? e) y = e 2 x , y (V) =? f) y = ln (1 + x), y (n) =? g) x = t 3, y = t 2, y ¢¢ xx =? h) x = cos t, y = sin t, y ¢¢ xx =?
ДИФФЕРЕНЦИАЛ
Понятие дифференциала Пусть функция у = f (x) определена в некоторой окрестности точки х 0. Тогда если существует такое число А, что приращение D у этой функции в точке х 0, соответствующее приращению D х аргумента, представимо в виде
Δ y = A ∙ D х + α (D х) ∙ D х,
где Нетрудно показать (положив у = х в выражение для приращения функции D у), что dх = D х. Функция у = f (x) дифференцируема в точке х 0 тогда и только тогда, когда в этой точке существует конечная производная f ¢ (x 0); при этом А = f ¢ (x 0). Поэтому d f (x 0) = f ¢ (x 0) × dх, или, если f ¢ (x) существует на интервале (a; b), то dу = f ¢ (x) dх, х Î (a; b).
Если приращение D х аргумента близко к нулю (т.е. достаточно мало), то приращение D у функции приближенно равно ее дифференциалу, т.е. D у» dу, откуда f (x 0 + D х)» f (x 0) + f ¢ (x 0) D х.
Эта формула удобна для приближенного вычисления значения функции и ее производной в точке х 0 . Пример 2. Вычислить приближенно ln 1,02. • f (x) = ln x => ln (x 0 + Δ x) ≈ ln x 0 + ≈ ln 1 +
Пример 3. Вычислить приближенно
Замечание. Значение приращения аргумента в тригонометрических функциях следует брать в радианах.
Правила Лопиталя 1-ое правило Лопиталя. Пусть функции f (x) и g (x) дифференцируемы в некоторой окрестностиU (х 0) точки х 0, кроме, быть может, самой этой точки, и g¢ (x) ¹ 0 причем 2-ое правило Лопиталя. Пусть функции f (x) и g (x) дифференцируемы в некоторой окрестностиU (х 0) точки х 0, кроме, быть может, самой этой точки, и g¢ (x) ¹ 0 Замечания. 1. Если отношение
2. Если имеет место неопределенность вида [0 ∙ ∞], то для применения правила Лопиталя ее предварительно надо свести к неопределенности вида
3. Если имеет место неопределенность вида [∞ – ∞], то для применения правила Лопиталя ее также предварительно сводят к неопределенности вида
4. Если имеет место неопределенность вида [00], [1∞], [∞0], [0∞], то для применения правила Лопиталя их надо свести к неопределенности вида
Примеры 2:
Примеры 3:
Формула Тейлора Пусть функция у = f (x) имеет в некоторой окрестности точки х 0 производные
равенство (при х → х 0).
Эта формула называется формулой Тейлора с остаточным членом в форме Пеано. Последнее слагаемое (т.е. остаточный член) в формуле Тейлора иногда записывают в виде
При х 0 = 0 формула Тейлора принимает вид и называется формулой Маклорена. Полезно помнить разложения по формуле Маклорена некоторых важнейших элементарных функций:
Экстремумы функции
Точка х 0 называется точкой локального максимума (локального минимума), если существует такая окрестность U (х 0) этой точки, что f (х) < f (х 0) (соответственно, f (х) > f (х 0)) " х Î U (х 0), х ¹ х 0. Точки локального максимума и минимума называются точками локального экстремума, а значения функции в этих точках – экстремумами функции.
Теорема Ферма (необходимое условие экстремума). Если х 0– точка локального экстремумадля функции f (x), то в этой точке производная функции либо равна нулю (f¢ (х 0) = 0), либо не существует.
Точки области определения функции f (х), в которых ее производная не существует или равна нулю, называются критическими точками функции.
Асимптоты
Прямая линия m называется асимптотой графика функции у = f (х), если расстояние d от точки М, лежащей на этом графике, до прямой m стремится к нулю при неограниченном удалении этой точки по графику от начала координат в бесконечность. Асимптоты бывают трех видов: вертикальные, наклонные и горизонтальные (рис.4). Вертикальная асимптота Наклонная асимптота Горизонтальная асимптота Рис.4.
Прямая х = х 0 называется вертикальной асимптотой графика функции f (х), если хотя бы один из односторонних пределов
Прямая y = kx + b называется наклонной асимптотой графика функции f (х) при х ® +¥ (х ® –¥), если
(соответственно,
Частным случаем наклонной асимптоты (при k = 0) является горизонтальная асимптота. Прямая y = bявляется горизонтальной асимптотой графикафункции у = f (х) при х ® +¥ (х ® – ¥) тогда и только тогда, когда
Построение графиков функций
При построении графика функции можно следующей схемой:
Исследование самой функции
1. Найти область определения функции ФУНКЦИИ И ИХ ГРАФИКИ Определение функции
Пусть каждому числу х из некоторого множества Х поставлено в соответствие определенное число у. Тогда говорят, что на множестве Х задана функция. Пишут: y = f (x).
Переменная х называется независимой переменной (аргументом), а переменная у зависимой. Множество Х называется областью определения данной функции и обозначается D (f), а множество всех чисел у, соответствующих различным числам х Если числу х 0 у 0 называется значением функции в точке х 0 (или при х = х 0). График функции
Пусть заданы прямоугольная система координат Оху и функция y = f (x). Графиком функции f (x) называется множество всех точек плоскости с координатами (х; f (x)), где х График функции y = f (x) зачастую можно построить с помощью преобразований (сдвиг, растяжение) графика некоторой уже известной функции. В частности: 1. График функции y = f (x) + а получается из графика функции y = f (x) сдвигом вдоль оси Оу на | a | единиц (вверх, если а > 0, и вниз, если а < 0). 2. График функции y = f (x – b) получается из графика функции y = f (x) сдвигом вдоль оси Оx на | b | единиц (вправо, если b > 0, и влево, если b < 0). 3. График функции y = k f (x) получается из графика функции y = f (x) растяжением вдоль оси Оу в k раз. 4. График функции y = f (mx) получается из графика функции y = f (x) сжатием по оси Ох в m раз. 5. График функции y = – f (x) получается из графика функции y = f (x) симметричным отражением относительно оси Ох. 6. График функции y = f (– x) получается из графика функции y = f (x) симметричным отражением относительно оси Оу.
Четность, нечетность и периодичность функции
Функция называется четной, если f (– x) = f (x). График четной функции симметричен относительно оси Оу.
Функция называется нечетной, если
|
||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 443; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.163.58 (0.271 с.) |
 Х, – областью значений этой функции и обозначается E (f).
Х, – областью значений этой функции и обозначается E (f). D (f).
D (f). х
х  Т,
Т, 











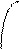
 Гиперболический синус: у = sh x =
Гиперболический синус: у = sh x =  .
.













 Гиперболический косинус: у = ch x =
Гиперболический косинус: у = ch x =  .
. =
=  .
. Гиперболический котангенс: у = cth x =
Гиперболический котангенс: у = cth x =  =
=  .
. .
.


 f (x) существует в том и только том случае, когда существуют и односторонние пределы
f (x) существует в том и только том случае, когда существуют и односторонние пределы  и
и  , причем все три предела равны.
, причем все три предела равны. = 1.
= 1.  = 1.
= 1. 
 = f (x 0).
= f (x 0). = f (x 0).
= f (x 0).




 Если существуют конечные односторонние пределы
Если существуют конечные односторонние пределы


 и
и  , но они не равны между
, но они не равны между




 а значение функции в этой точке не совпадает с односторонними пределами, то х 0 называется точкой разрыва 1-го рода.
а значение функции в этой точке не совпадает с односторонними пределами, то х 0 называется точкой разрыва 1-го рода.

 Если в точке х 0 существует конечный предел
Если в точке х 0 существует конечный предел  ,
,





 а f (x 0) не определено или
а f (x 0) не определено или 





 из односторонних пределов (функция «убегает» …
из односторонних пределов (функция «убегает» …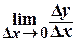 =
= 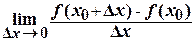 .
. =
= 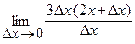 = 3
= 3  (2 х + Δ х) = 3 ∙ 2 x = 6 x.
(2 х + Δ х) = 3 ∙ 2 x = 6 x. cos
cos  =>
=> =
= 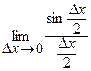 ∙
∙  = cos x.
= cos x.
 => y′ = y ∙ (ln y)′.
=> y′ = y ∙ (ln y)′.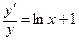 => y′ = y (ln x + 1) или
=> y′ = y (ln x + 1) или

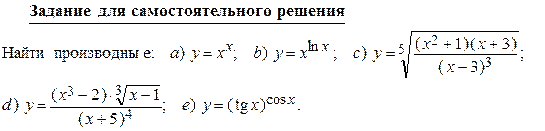
 .
.
 =
=  .
.
 α (D х) = 0 (α (D х) – б.м.ф.), то функция у = f (x) называется дифференцируемойв точке х 0. При этом главная, линейная относительно D х,часть этого приращения, т.е. А × D х, называется дифференциалом функции в точке х 0 и обозначается dy или d f (x 0).
α (D х) = 0 (α (D х) – б.м.ф.), то функция у = f (x) называется дифференцируемойв точке х 0. При этом главная, линейная относительно D х,часть этого приращения, т.е. А × D х, называется дифференциалом функции в точке х 0 и обозначается dy или d f (x 0).
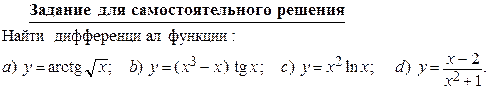
 ∙ Δ x || x 0 = 1, Δ x = 0,02 || => ln 1,02 ≈
∙ Δ x || x 0 = 1, Δ x = 0,02 || => ln 1,02 ≈ ∙ 0,02 = 0,02.
∙ 0,02 = 0,02. .
.

 х Î U (х 0), х ¹ х 0. Тогда, если
х Î U (х 0), х ¹ х 0. Тогда, если  =
=  = 0 (неопределенность вида
= 0 (неопределенность вида  ) и существует
) и существует  , то существует и
, то существует и 
 ) и существует
) и существует  , в свою очередь, представляет собой неопределенность вида
, в свою очередь, представляет собой неопределенность вида  = 0, а
= 0, а = ∞, то
= ∞, то 







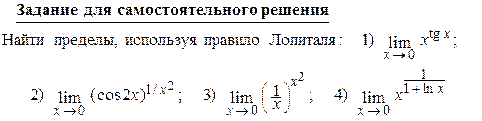

 (в этом случае надо дополнительно предполагать существование f ( n + 1)(x) в данной окрестности точки х 0). Соответствующая формула тогда называется формулой Тейлора с остаточным членом в форме Лагранжа.
(в этом случае надо дополнительно предполагать существование f ( n + 1)(x) в данной окрестности точки х 0). Соответствующая формула тогда называется формулой Тейлора с остаточным членом в форме Лагранжа.







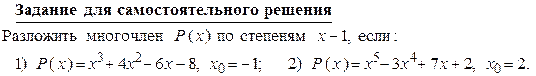







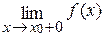 и/или
и/или  равен бесконечности.
равен бесконечности.
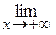 | f (x) – (kx + b) | = 0 (соответственно,
| f (x) – (kx + b) | = 0 (соответственно, | f (x) – (kx + b) | = 0). Прямая y = kx + b является наклонной асимптотойграфика функцииf (х) при х ® +¥ (х ® – ¥) тогда и только тогда, когда существуют пределы
| f (x) – (kx + b) | = 0). Прямая y = kx + b является наклонной асимптотойграфика функцииf (х) при х ® +¥ (х ® – ¥) тогда и только тогда, когда существуют пределы
 = k и
= k и 





