
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Производная функций, заданных параметрически
Пусть функция у = f (x) определена параметрически функциями х = х (t) и у = у (t). Тогда, если функции х = х (t) и у = у (t) имеют производные в точке t 0, причем х ¢ (t) ¹ 0, а функция у = f (x) имеет производную в точке х 0 = х (t 0), то эта производная находится по формуле
Пример 6. Найти производную y ′(x) от функции, заданной параметрически: x = 2cos t, y = 3sin t. • y ′(x) =
Задание для самостоятельного решения Найти у ¢ (х) для заданных параметрически функций у = у (х): a) x = t 3 + t, y = t 2 + t + 1; b) x = t – sin t, y = 1 – cos t; c) x = et sin t, y = et cos t; d) x = sin2 t, y = sin2 t; e) x = 5 sh t, y = 4 ch t.
Геометрический смысл производ Пусть функция y = f (x) имеет производную в точке х 0. Тогда существует касательная к графику этой функции в точке М 0 (х 0; у 0), уравнение которой имеет вид
y – у 0 = f ¢(x 0) (x – x 0). При этом f ¢(x 0) = tg a, где a - угол наклона этой касательной к оси Ох.
Прямая, проходящая через точку касания, перпендикулярно касательной, называется нормалью к кривой и имеет уравнение y – у 0 = – Если f ¢(x 0) = 0 (т.е. касательная горизонтальна), то нормаль вертикальна и имеет уравнение x = x 0. Пусть даны две пересекающиеся в точке М 0 (х 0; у 0) кривые y = f 1 (x) и y = f 2 (x), причем обе функции имеют производные в точке х 0. Тогда углом междуэтимикривыми называется угол между касательными к ним, проведенными в точке М 0. Этот угол можно найти из формулы
tg j = (f¢ 2 (x 0) - f¢ 1 (x 0)) / (1 + f¢ 1 (x 0) × f¢ 2 (x 0)).
Пример 7. Написать уравнения касательной и нормали к параболе у 2 = 4 х в точке М (1; 2).
• Находим у ¢ (х) как производную неявной функции: (у 2 ) ¢ = (4 х) ¢, т.е. 2 у у ¢ = 4 => у ¢ = 2 / y. Значит, у ¢ (х 0) = у ¢ (1) = 1. Отсюда получаем уравнение касательной в точке М y – 2 = 1(x – 1) => y = x + 1. Уравнение нормали: y – 2 = –1(x – 1) => y = – x + 3.
Производные высших порядков Производная f ¢(x) от функции f (x) называется также производной первого порядка. В свою очередь производная от функции f ¢ (x) называется производной второго порядка от функции f (x) (или второйпроизводной) и обозначается f¢¢ (x). Аналогично определяется производная третьего порядка (или третьяпроизводная), обозначаемая f¢¢¢ (x) и т.д. Производная n -ого порядка обозначается f ( n )(x).
Для функции, заданной параметрически (x = x (t), y = у (t)), вторая производная у¢¢ (x) находится по формуле Пример 10. Найти: а) f ¢¢¢ (x), где f (x) = sin 3 x; b) y¢¢xx дляфункции у = у (х), заданной параметрически x = t 2, y = t 3.
· a) Находим первую производную f ¢(х) = (sin 3 x) ¢ = 3 cos 3 x. отсюда получаем вторую производную f ¢¢(х) = (3 cos 3 x) ¢ = – 9 sin 3 x, а затем искомую третью: f ¢¢¢(х) = (– 9 sin 3 x) ¢ = – 27 cos 3 x.
Задание для самостоятельного решения
Найти производные указанных порядков для следующих функций: a) y = tg 3 x, y ¢¢ =? b) y = – x cos x, y ¢¢ =? c) y = ln2 x, y ¢¢ =? d) y = x × ln x, y ¢¢¢ =? e) y = e 2 x , y (V) =? f) y = ln (1 + x), y (n) =? g) x = t 3, y = t 2, y ¢¢ xx =? h) x = cos t, y = sin t, y ¢¢ xx =?
ДИФФЕРЕНЦИАЛ
Понятие дифференциала Пусть функция у = f (x) определена в некоторой окрестности точки х 0. Тогда если существует такое число А, что приращение D у этой функции в точке х 0, соответствующее приращению D х аргумента, представимо в виде
Δ y = A ∙ D х + α (D х) ∙ D х,
где Нетрудно показать (положив у = х в выражение для приращения функции D у), что dх = D х. Функция у = f (x) дифференцируема в точке х 0 тогда и только тогда, когда в этой точке существует конечная производная f ¢ (x 0); при этом А = f ¢ (x 0). Поэтому d f (x 0) = f ¢ (x 0) × dх, или, если f ¢ (x) существует на интервале (a; b), то dу = f ¢ (x) dх, х Î (a; b).
Если приращение D х аргумента близко к нулю (т.е. достаточно мало), то приращение D у функции приближенно равно ее дифференциалу, т.е. D у» dу, откуда f (x 0 + D х)» f (x 0) + f ¢ (x 0) D х.
Эта формула удобна для приближенного вычисления значения функции и ее производной в точке х 0 . Пример 2. Вычислить приближенно ln 1,02. • f (x) = ln x => ln (x 0 + Δ x) ≈ ln x 0 + ≈ ln 1 +
Пример 3. Вычислить приближенно
Замечание. Значение приращения аргумента в тригонометрических функциях следует брать в радианах.
|
||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 1015; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.216.163 (0.015 с.) |

 =
= 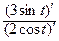 = –
= –  = –1,5 ctg t.
= –1,5 ctg t.










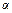
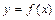




 ной
ной (x – x 0 ).
(x – x 0 ).



 =
=  .
.
 α (D х) = 0 (α (D х) – б.м.ф.), то функция у = f (x) называется дифференцируемойв точке х 0. При этом главная, линейная относительно D х,часть этого приращения, т.е. А × D х, называется дифференциалом функции в точке х 0 и обозначается dy или d f (x 0).
α (D х) = 0 (α (D х) – б.м.ф.), то функция у = f (x) называется дифференцируемойв точке х 0. При этом главная, линейная относительно D х,часть этого приращения, т.е. А × D х, называется дифференциалом функции в точке х 0 и обозначается dy или d f (x 0).
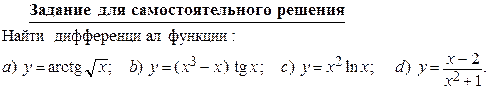
 ∙ Δ x || x 0 = 1, Δ x = 0,02 || => ln 1,02 ≈
∙ Δ x || x 0 = 1, Δ x = 0,02 || => ln 1,02 ≈ ∙ 0,02 = 0,02.
∙ 0,02 = 0,02. .
.




