
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Законы Ома и Кирхгофа в комплексной формеСодержание книги Поиск на нашем сайте
Закон Ома устанавливает связь между током и напряжением на участке цепи. Закон Ома для участка цепи не содержащего источника ЭДС (рис.). z – комплексное сопротивление участка цепи.
Закон Ома для участка цепи, содержащих источник ЭДС (рис.).
Закон Ома позволяет определить ток на этом участке цепи.
Члены алгебраической суммы
Законы Кирхгофа. Первый закон Кирхгофа (для узла): алгебраическая сумма комплексных амплитуд тока в узле равна нулю.
Второй закон Кирхгофа (для контура): алгебраическая сумма падений напряжений на пассивных элементах контура равна алгебраической сумме источников э.д.с. входящих в контур.
При составлении уравнений по второму закону Кирхгофа: 1) выбирают условно положительное направление обхода элементарного контура; 2) члены суммы 3) слагаемые правой суммы 4.3. Эквивалентные преобразования электрических цепей Электрические цепи считают простыми, если они содержат только последовательное или только параллельное соединение элементов. Участок цепи, содержащий и параллельное, и последовательное соединение элементов называют сложным или участком со смешанным соединением элементов. Преобразования электрических цепей считают эквивалентными, если при их выполнении напряжения и токи на интересующих нас участках не изменяются. При преобразовании сложных электрических цепей пользуются последовательным методом, то есть последовательно преобразуют участки цепи, имеющие простое соединение элементов.
4.3.1. Эквивалентное преобразование схемы при последовательном соединении элементов
Рассмотрим комплексную схему замещения электрической цепи, состоящей из последовательного соединения отдельных элементов (рис. 4.). Данная цепь представляет собой контур, у которого через все элементы протекает общий для всех элементов ток. Эквивалентно преобразуем схему к одному элементу, но так чтобы напряжение и ток на выводах схемы сохранили свои значения. Это возможно, когда сопротивление исходной цепи и эквивалентной цепи одинаковы. На основании закона Ома и второго закона Кирхгофа в комплексной форме можно записать уравнение электрического равновесия
Напряжение и ток для обеих схем одинаковы, когда
Вывод. При эквивалентном преобразовании, при последовательном соединении элементов их комплексные сопротивления складываются. 1) Эквивалентное преобразование сопротивлений
Учитывая, что Z R=R, и соотношение полученное выше, получим Rэкв=R1+R2. 2) Эквивалентное преобразование емкостей.
Учитывая, что Z С=1/(jωC), и соотношение полученное выше, получим 3) Эквивалентное преобразование индуктивностей
Учитывая, что Z L=jωL, и соотношение полученное выше, получим Lэкв=L1+L2. 4.3.2. Эквивалентное преобразование схемы при параллельном соединении элементов Рассмотрим комплексную схему замещения электрической цепи, состоящей из параллельного соединения отдельных элементов (рис. 4.). Данная цепь содержит два узла, между которыми включены все элементы. Общим для всех элементов является напряжение на них. Эквивалентно преобразуем схему к одному элементу, но так чтобы напряжение и ток на выводах схемы сохранили свои значения. Это возможно, когда сопротивление исходной цепи и эквивалентной цепи одинаковы. На основании закона Ома и первого закона Кирхгофа в комплексной форме можно записать уравнение электрического равновесия
I=I1+I2+…+In, или (U/ Z экв) = (U/ Z 1) + (U/ Z 2) + …(U/ Z n). Отсюда получим, что (1/ Z экв) = (1/ Z 1) + (1/ Z 2) + … +(1/ Z n), или Z экв = 1/[(1/ Z 1) + (1/ Z 2) + … +(1/ Z n)]. Учитывая, (1/ Z) = Y – комплексная проводимость элемента, можно записать, что Y экв = Y 1 + Y 2 + … + Y n. Вывод. При эквивалентном преобразовании, при параллельном соединении элементов их комплексные проводимости складываются. 1)Эквивалентное преобразование сопротивлений
Учитывая, что Z R=R, и соотношение полученное выше, получим Rэкв=R1R2/(R1+R2). 2) Эквивалентное преобразование емкостей
3) Эквивалентное преобразование индуктивностей
Учитывая, что Z L=jωL, и соотношение полученное выше, получим Lэкв=L1L2/(L1+L2). 4.3.3. Эквивалентное преобразование схемы при смешанном соединении элементов
Эквивалентное сопротивление находим методом последовательных эквивалентных преобразований. Этот методсостоит в поэтапном преобразовании простых участков цепи. Они показаны на рис.1.6. 4.3.4. Эквивалентное преобразование источников электрических сигналов
Схему 1 можно заменить схемой 2, если параметры схемы2 выбраны из условий: I = E/ Z i1, Z i2 = Z i1. Схему 2 можно заменить схемой 1, если параметры схемы1 выбраны из условий: E =I Z i1, Z i1 = Z i2.
|
||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 360; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.190.253.224 (0.008 с.) |


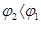

 - напряжение на данном участке цепи.
- напряжение на данном участке цепи.

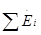 берутся с знаком «+», если направления ЭДС и тока совпадают, и с знаком «–», если не совпадает.
берутся с знаком «+», если направления ЭДС и тока совпадают, и с знаком «–», если не совпадает.
 - арифметическая суммы комплексных сопротивлений на данном участке, все члены суммы берутся с знаком “+”.
- арифметическая суммы комплексных сопротивлений на данном участке, все члены суммы берутся с знаком “+”.
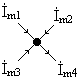 При записи первого закона Кирхгофа пользуются следующим правилом: токи, втекающие в узел берутся с знаком «+», а вытекающие с знаком «-»
При записи первого закона Кирхгофа пользуются следующим правилом: токи, втекающие в узел берутся с знаком «+», а вытекающие с знаком «-»

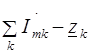 берутся со знаком “+”, если ток через элемент и направление обхода совпадает, со знаком “-“ в противном случае;
берутся со знаком “+”, если ток через элемент и направление обхода совпадает, со знаком “-“ в противном случае; берутся со знаком “+”, если направление источника э.д.с. и направление обхода совпадают и со знаком “-“ в противном случае.
берутся со знаком “+”, если направление источника э.д.с. и направление обхода совпадают и со знаком “-“ в противном случае.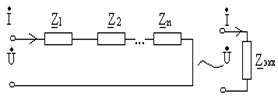

 .
. Рассмотрим электрическую цепь схема, которой приведена на рис.4. Эквивалентно преобразуем сопротивления R1и R2 к одному сопротивлению Rэкв.
Рассмотрим электрическую цепь схема, которой приведена на рис.4. Эквивалентно преобразуем сопротивления R1и R2 к одному сопротивлению Rэкв.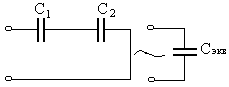 Рассмотрим электрическую цепь схема, которой приведена на рис.4. Эквивалентно преобразуем емкости С1и С2 к одной эквивалентной емкости Сэкв.
Рассмотрим электрическую цепь схема, которой приведена на рис.4. Эквивалентно преобразуем емкости С1и С2 к одной эквивалентной емкости Сэкв. .
. Рассмотрим электрическую цепь схема, которой приведена на рис.4. Эквивалентно преобразуем индуктивности L1и L2 к одной эквивалентной индуктивности Lэкв.
Рассмотрим электрическую цепь схема, которой приведена на рис.4. Эквивалентно преобразуем индуктивности L1и L2 к одной эквивалентной индуктивности Lэкв. Рассмотрим электрическую цепь схема, которой приведена на рис.4. Эквивалентно преобразуем сопротивления R1и R2 к одному сопротивлению Rэкв.
Рассмотрим электрическую цепь схема, которой приведена на рис.4. Эквивалентно преобразуем сопротивления R1и R2 к одному сопротивлению Rэкв. Рассмотрим электрическую цепь схема, которой приведена на рис.4. Эквивалентно преобразуем емкости С1и С2 к одной эквивалентной емкости Сэкв. Учитывая, что Z С=1/(jωC), и соотношение полученное выше, получим Cэкв = C1 + С2.
Рассмотрим электрическую цепь схема, которой приведена на рис.4. Эквивалентно преобразуем емкости С1и С2 к одной эквивалентной емкости Сэкв. Учитывая, что Z С=1/(jωC), и соотношение полученное выше, получим Cэкв = C1 + С2. Рассмотрим электрическую цепь схема, которой приведена на рис.4. Эквивалентно преобразуем индуктивности L1и L2 к одной эквивалентной индуктивности Lэкв.
Рассмотрим электрическую цепь схема, которой приведена на рис.4. Эквивалентно преобразуем индуктивности L1и L2 к одной эквивалентной индуктивности Lэкв. Такое преобразование выполняется последовательным методом, т.е. последовательно преобразуются участки цепи имеющее простое соединение элементов. Рассмотрим такое преобразование на примере, для обобщенной двухконтурной цепи, представленной комплексной схемой замещения (рис.1.5)
Такое преобразование выполняется последовательным методом, т.е. последовательно преобразуются участки цепи имеющее простое соединение элементов. Рассмотрим такое преобразование на примере, для обобщенной двухконтурной цепи, представленной комплексной схемой замещения (рис.1.5)
 Любой источник электрического сигнала может быть представлен одной из двух схем (рис. 4. – схема 1 и рис. 4. – схема 2), поскольку при определенном выборе параметров элементов эти схемы эквивалентны, т.е. ток нагрузки Iн и напряжение на нагрузки Uн в этих схемах одинаковы.
Любой источник электрического сигнала может быть представлен одной из двух схем (рис. 4. – схема 1 и рис. 4. – схема 2), поскольку при определенном выборе параметров элементов эти схемы эквивалентны, т.е. ток нагрузки Iн и напряжение на нагрузки Uн в этих схемах одинаковы.


