Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общая схема исследования и построения графика функции заданной явно.Содержание книги
Поиск на нашем сайте
Общее исследование функции следует проводить по приведенной ниже схеме: 1.Определить область существования функции, область непрерывности, точки разрыва. 2. Найти асимптоты функции. 3. Выяснить вопрос о периодичности. 4. Выяснить вопрос о четности или нечетности. В случае, если функция окажется четной 5.Найти точки пересечения графика функции с осями координат: с осью абсцисс - точки с осью ординат- точки 6. Найти промежутки монотонности и локальные экстремумы. 7.Найти интервалы выпуклости и вогнутости, точки перегиба. 8. Составить таблицу
Точки 9.На основании проведенного исследования построить график заданной функции. Пример 26 Провести полное исследование и построить график функции
Решение: Область определения функции
Точка разрыва функции 2. Асимптоты. Вертикальная асимптота Поведение функции в окрестности
Найдем наклонную асимптоту:
Прямая 3. Функция не является периодической. 4. Четность функции
Условие четности или нечетности не выполнено. Заданная функция –функция общего вида.
5. Точки пересечения с осями.
График функции проходит через начало координат.
6. Промежутки монотонности, локальные экстремумы.
Найдем критические точки:
Найдем значения функции в критических точках:
7.Промежутки выпуклости и вогнутости. Точки перегиба. Найдем вторую производную.
Точки, в которых Исследуем знак второй производной методом интервалов:
8. Составляем таблицу.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 227; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.246.148 (0.006 с.) |

 или нечетной
или нечетной  достаточно исследовать функцию только при положительных значениях аргумента. При построении графика следует учесть, что график четной функции симметричен относительно оси ординат; график нечетной функции симметричен относительно начала координат.
достаточно исследовать функцию только при положительных значениях аргумента. При построении графика следует учесть, что график четной функции симметричен относительно оси ординат; график нечетной функции симметричен относительно начала координат.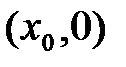 , где
, где  -решение уравнения
-решение уравнения  ;
; , где
, где  .
.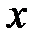







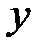
















 -все найденные в п.6-7 точки, в которых производные обращаются в нуль или не существуют.
-все найденные в п.6-7 точки, в которых производные обращаются в нуль или не существуют. .
.
 , функция непрерывна на
, функция непрерывна на  и
и 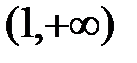 .
.



 является наклонной асимптотой заданной кривой.
является наклонной асимптотой заданной кривой.






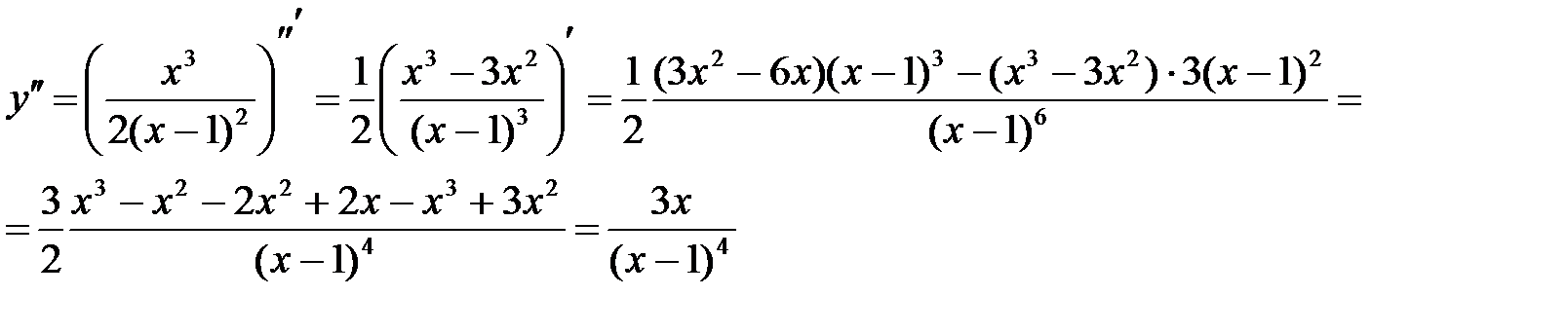
 равна нулю или несуществует:
равна нулю или несуществует: