
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Производная сложной функции.Содержание книги Поиск на нашем сайте
Если
В случае
Аналогично во всех более сложных случаях.
Пример 1 Найти производную функции Решение: Аргументом данной функции Используя таблицу производных, имеем:
Производную функции
Таким образом, получаем, согласно (6):
Ответ: Задания 2. Найти производные функции:
Производная функции, заданной неявно. Пусть зависимость между
В этом случае говорят, что функция Для вычисления производной а) вычислить производные от обеих частей уравнения (8), считая при этом б) приравнять полученные производные; в) решить полученное уравнение относительно
Пример 2 Найти производную Решение: а) вычисляем производные от обеих частей заданного равенства, считая
б) приравниваем полученные производные:
в) решаем уравнение относительно
Ответ:
Производная функции, заданной параметрически.
Функция
Если
Пример 3 Найти производную
Решение: Находим
Воспользовавшись формулой (10), получаем:
Ответ:
Производная степенно-показательной функции. Рассмотрим степенно-показательную функцию Для вычисления производной
Продифференцируем обе части полученного равенства, считая при этом
Разрешая полученное уравнение относительно
Пример 4 Найти производную функции Решение: Прологарифмируем заданную функцию:
Продифференцируем обе части полученного равенства по
Приравниваем полученные производные:
Учитывая явный вид заданной функции, окончательно получаем:
Ответ: Задания 3. Найти производные функции:
Производные высших порядков. Производной второго порядка или второй производной функции
Аналогично определяются производные третьего, четвертого и, вообще, любого
Производная
Производная
Пример 5 Найти производную второго порядка функции Решение: Найдем первую производную заданной функции:
Найдем вторую производную согласно (12):
Ответ: Пример 6 Найти производную Решение:
Подставим найденные производные в формулу (15). Тогда
Ответ:
Если
где Для вычисления второй производной функции, заданной параметрически, можно также использовать формулу
Пример 7 Найти производную второго порядка
Решение: Найдем
Воспользовавшись формулой (10), получаем
Найдем
Ответ: Задания 4. Найти производные функций указанного порядка:
Применяя формулу Лейбница, найти производные функций n-го порядка:
Найти производные 2-го порядка
Дифференциал функции. Вычисление дифференциала. Приращение
Произведение функции и обозначается следующим образом:
Правила вычисления дифференциала имеют вид:
Пример 8 Найти дифференциал функции
Решение:
Для того, чтобы вычислить дифференциал по формуле (19), найдем производную заданной функции:
Тогда,согласно (19) получаем:
Ответ: Пример 9 Найти дифференциал функции, заданной неявно:
Решение:
Для того, чтобы вычислить дифференциал по формуле (19), найдем Воспользуемся правилом вычисления производной, приведенным в 3. а) вычисляем производные от обеих частей заданного уравнения, считая при этом
б) приравниваем полученные производные:
в) решаем полученное уравнение относительно
Тогда,согласно (19) получаем:
Ответ:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 369; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.154.238 (0.007 с.) |

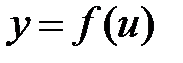 и
и  являются дифференцируемыми функциями своих аргументов, то производная сложной функции
являются дифференцируемыми функциями своих аргументов, то производная сложной функции  существует и равна произведению производной данной функции
существует и равна произведению производной данной функции  по промежуточному аргументу
по промежуточному аргументу  на производную промежуточного аргумента
на производную промежуточного аргумента  (6)
(6)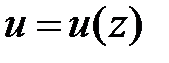 ,
,  :
: (7)
(7)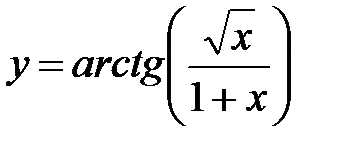
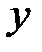 является
является 
 .
.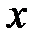 найдем, используя правило дифференцирования частного (3) и таблицу производных:
найдем, используя правило дифференцирования частного (3) и таблицу производных:










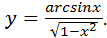
 .
.

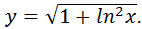
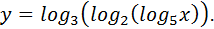






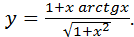
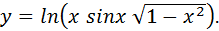

 (8)
(8) задана неявно.
задана неявно. необходимо:
необходимо:


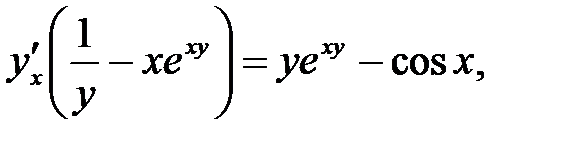


 :
: (9)
(9)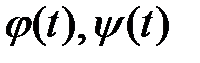 - дифференцируемые функции и
- дифференцируемые функции и  , то производная
, то производная  (10)
(10)
 :
:


 .
.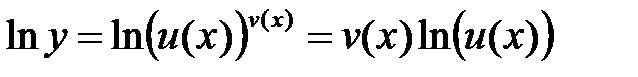

 (11)
(11)















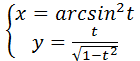

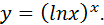



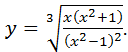
 называется производная от ее производной
называется производная от ее производной  :
: (12)
(12) -го порядка:
-го порядка: (13)
(13) (14)
(14)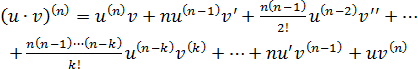 (15)
(15) .
.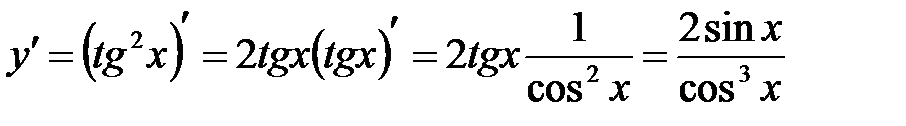


 .
.




 задана параметрически в виде (9), то производная второго порядка может быть вычислена как
задана параметрически в виде (9), то производная второго порядка может быть вычислена как , (16)
, (16) определена по формуле (10).
определена по формуле (10). (17)
(17) , если
, если

 :
:
 :
:

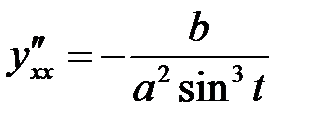

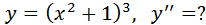
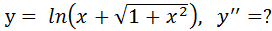









 функций заданных параметрически:
функций заданных параметрически:



 функции
функции  может быть представлено в виде
может быть представлено в виде (18)
(18) , представляющее собой, так называемую главную часть приращения, линейную относительно
, представляющее собой, так называемую главную часть приращения, линейную относительно  , называют дифференциалом
, называют дифференциалом (19)
(19)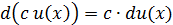 (20)
(20) (21)
(21) (22)
(22)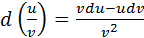 (23)
(23)
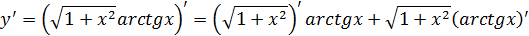


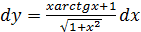

 .
.






 .
.


