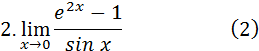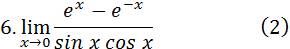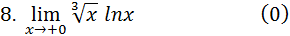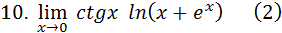Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Применение дифференциала к приближенным вычислениям.Содержание книги
Поиск на нашем сайте
Согласно формуле (18) в случае, когда
Учитывая, что
Получаем формулу, для приближенного вычисления значения функции в точке
Пример 10 Насколько приблизительно изменилась сторона квадрата, если его площадь увеличилась от 9 м2 до 9,1м2? Решение: Обозначим через Тогда
По условию Приращение
Тогда
Ответ: Сторона квадрата увеличилась приблизительно на 0,016 м. Пример 11 Найти приближенное значение Решение:
Воспользуемся формулой (25). В данном случае Найдем
Тогда, согласно (25) получаем:
Ответ:
Дифференциалы высших порядков. Дифференциалом второго порядка называется дифференциал, от дифференциала первого порядка:
Аналогично определяются дифференциалы третьего, четвертого и, вообще любого Если
Пример 12. Вычислить Решение: а)
тогда, согласно (26)
б)
По формуле (27) получаем
Ответ: а)
Задания 5. Найти дифференциалы функции:
Найти дифференциалы функции, заданных неявно:
Найти дифференциалы 2-го порядка:
Найти
Вычислить приближенно с помощью дифференциала:
17. Найти точное и приближенное изменение объёма шара при изменении его радиуса с
Правило Лопиталя – Бернулли. 8.1 Раскрытие неопределенностей типа Пусть Если
при условии, что предел отношения производных существует. При необходимости формула (29) может быть применена к полученным отношениям несколько раз. Пример 13 Вычислить предел Решение: В данном случае
Ответ:
8.2 Раскрытие неопределенности типа
Для раскрытия неопределенности типа
и далее воспользуемся правилом Лопиталя – Бернулли (29). Пример 14 Вычислить предел Решение: В данном случае
В результате получили неопределенность типа Применяя правило Лопиталя - Бернулли, получаем:
Ответ:
8.3 Раскрытие неопределенности типа
Для раскрытия неопределенности типа
Если
Предел (32) представляет собой неопределенность типа Пример 15 Вычислить предел Решение: Преобразуем выражение, стоящее под знаком предела, согласно изложенной схеме:
Для упрощения вычислений воспользуемся эквивалентностью бесконечно малых при
Тогда
8.4 Раскрытие неопределенностей типа
Неопределенности указанного типа раскрываются с помощью предварительного логарифмирования:
В результате получаем неопределенность типа
Пример 16 Вычислить предел Решение: В данном случае
т.е. имеем неопределенность типа Прологарифмируем функцию, стоящую под знаком предела и преобразуем полученное выражение в частное:
Получили неопределенность типа
Таким образом, получаем
Следовательно,
Ответ: Задания 6. Найти пределы, используя правило Лопиталя – Бернулли:
|
||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 303; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.164.229 (0.007 с.) |

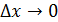 , приращение функции
, приращение функции  в точке
в точке  можно считать приближенно равным ее дифференциалу (
можно считать приближенно равным ее дифференциалу (
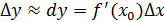 (24)
(24)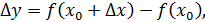
 , близкой к точке
, близкой к точке  (25)
(25) - его сторону.
- его сторону.
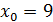 ;
; 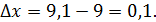
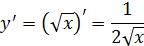

 .
. .
. . В качестве
. В качестве  . Тогда
. Тогда  ,
,  .
. :
:
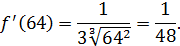

 .
.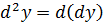 (26)
(26)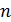 -го порядка.
-го порядка. и
и  (27)
(27)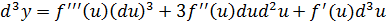 (28)
(28) в случае если а)
в случае если а) 
 -независимая переменная
-независимая переменная
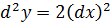
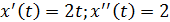

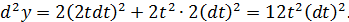
 б)
б) 
 .
.


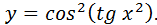
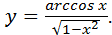

 .
.

 .
.

 функции
функции  в случае если
в случае если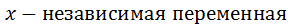 .
.

 . 14 .arctg 1,02.
. 14 .arctg 1,02.
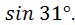 16.
16. 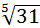 .
.
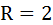 до
до 
 и
и  .
.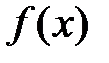 и
и 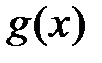 -дифференцируемые функции, причем
-дифференцируемые функции, причем  .
.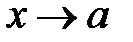 , тогда
, тогда (29)
(29) .
. . При
. При  имеем неопределенность типа
имеем неопределенность типа 

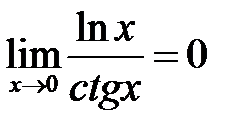
 .
. , где
, где  ,
,  , в частное:
, в частное: или
или  (30)
(30) .
.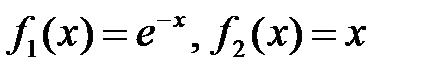 . При
. При  имеем неопределенность типа
имеем неопределенность типа  . Преобразуем произведение
. Преобразуем произведение  в частное
в частное
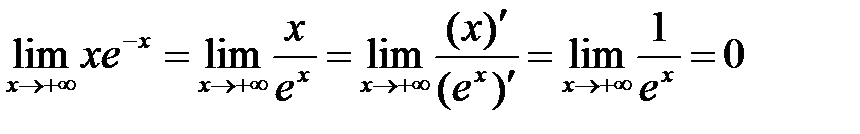 .
.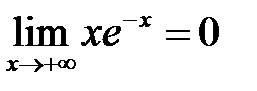
 .
.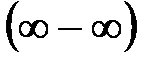 разность
разность  преобразуем в произведение:
преобразуем в произведение: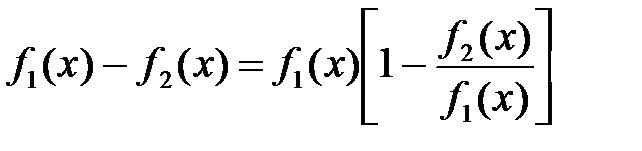 (31)
(31) , то произведение (31) может быть преобразовано в частное:
, то произведение (31) может быть преобразовано в частное: (32)
(32) .
.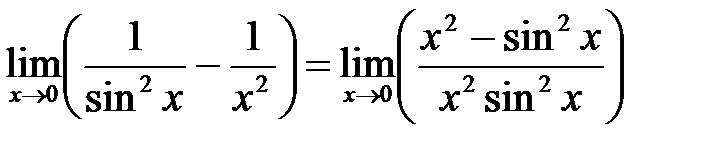
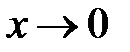 :
:
 Ответ:
Ответ: 
 .
. (33)
(33)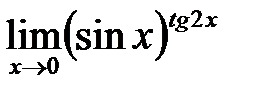 .
. ,
, 
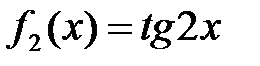 ,
, 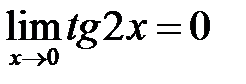
 .
. .
.
 .
.