Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Промежутки монотонности функции. Экстремумы функции.Содержание книги
Поиск на нашем сайте Условие монотонности функции: Для того, чтобы дифференцируемая на
Для того, чтобы дифференцируемая на
Промежутки, на которых производная функции сохраняет определенный знак, называются промежутками монотонности функции Пример 19 Найти промежутки монотонности функции Решение: Найдем производную функции
Найдем промежутки знакопостоянства полученной производной. Для этого разложим полученный квадратный трехчлен на множители:
Исследуем знак полученного выражения, используя метод интервалов.
Таким образом, получаем согласно (36), (37),что заданная функция возрастает на Ответ: Заданная функция Определение Функция ( Локальный минимум или максимум функции Необходимое условие существования экстремума. Пусть функция Точка
Достаточные условия наличия экстремума в критической точке Пусть точка Первое достаточное условие экстремума: Пусть функция Точка производная функции меняет знак с плюса на минус. Точка производная функции меняет знак с минуса на плюс. Пример 20 Найти экстремумы функции Решение: Найдем производную заданной функции
Приравнивая в полученной производной к нулю числитель и знаменатель, найдем критические точки:
Исследуем знак производной, используя метод интервалов.
Из рисунка видно, что при переходе через точку При переходе через точку Следовательно, в точке При переходе через точку Ответ:
Второе достаточное условие экстремума: Если первые если
то если
то Пример 21 Найти экстремумы функции, пользуясь второй производной Решение: ОДЗ: Найдем первую производную заданной функции
Найдем критические точки функции:
Точку Найдем вторую производную
Находим Таким образом, на основании (39) делаем вывод о том, что при Ответ: Задания 8. Исследовать на возростание и убывание функции:
Исследовать на экстремумы функции:
|
||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 260; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.87.167 (0.012 с.) |

 функция
функция 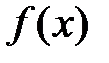 не возрастала, необходимо и достаточно, чтобы во всех точках, принадлежащих
не возрастала, необходимо и достаточно, чтобы во всех точках, принадлежащих  (36)
(36) (37)
(37) .
. .
.
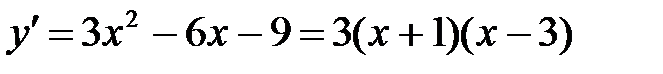 .
.
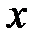
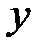
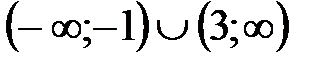 и убывает на
и убывает на  .
. локальный максимум (минимум), если существует такая окрестность точки
локальный максимум (минимум), если существует такая окрестность точки  , что для всех
, что для всех  выполняется условие
выполняется условие 
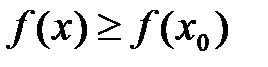 ).
). в точке
в точке  .
. .
.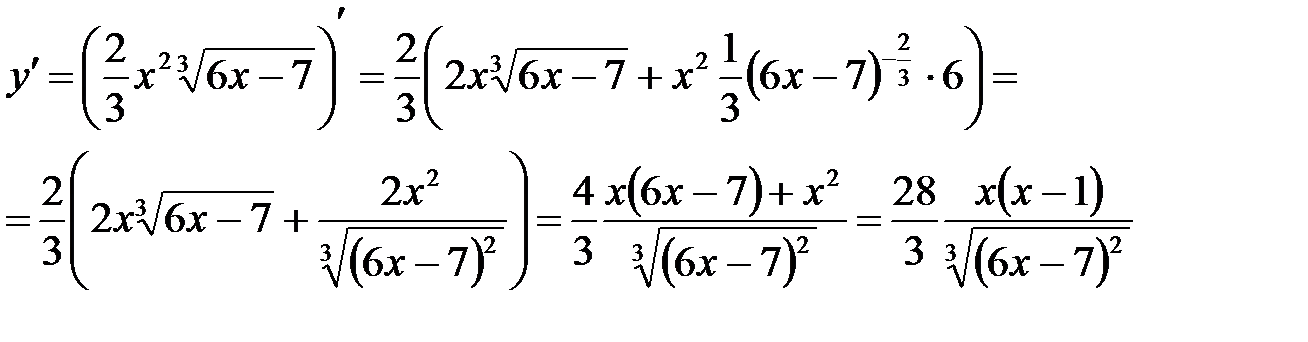
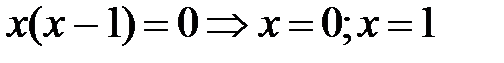

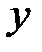

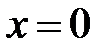 производная меняет знак с плюса на минус. Следовательно, в точке
производная меняет знак с плюса на минус. Следовательно, в точке  производная меняет знак с минуса на плюс.
производная меняет знак с минуса на плюс. - локальный минимум.
- локальный минимум. производная не меняет знак. Следовательно, критическая точка
производная не меняет знак. Следовательно, критическая точка  не является экстремумом заданной функции.
не является экстремумом заданной функции.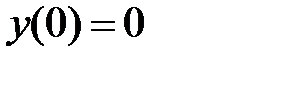 - локальный максимум,
- локальный максимум,  - локальный минимум.
- локальный минимум. производные функции
производные функции  в точке
в точке  -ная производная функции
-ная производная функции  , (38)
, (38) , (39)
, (39) .
. .
.
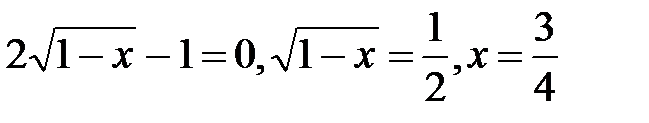
 мы не рассматриваем, так как функция определена только в левой окрестности
мы не рассматриваем, так как функция определена только в левой окрестности 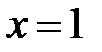 .
.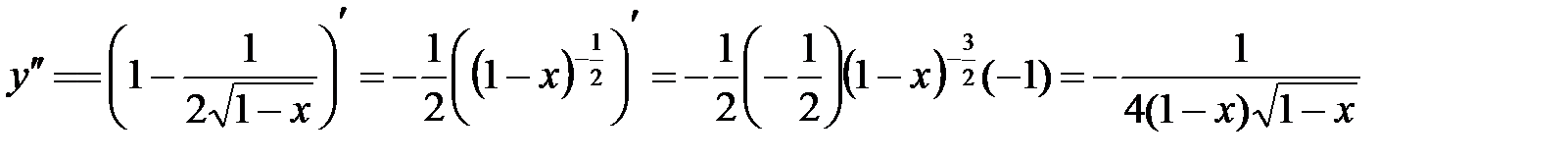

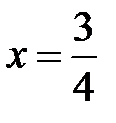
 - локальный максимум.
- локальный максимум. - локальный максимум.
- локальный максимум.