
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод Ньютона (метод касательных) для решения нелинейного уравнения.Содержание книги
Поиск на нашем сайте
Пусть дано уравнение f(x)=0 и начальное приближение x0 к его корню. Предполагаем, что функция f(x) — вещественная и находим вещественный корень x*. Будем предполагать, что на отрезке [a,b] (x0Î[a,b]) содержится единственный корень уравнения f(x)=0 и существуют непрерывные производные f'(x)¹0, f''(x)¹0. Заменим уравнение в окрестности x0 приближенно уравнением f(x0)+f'(x0)(x-x0)=0, левая часть которого есть линейная часть разложения функции f(x) в ряд Тейлора в окрестности точки x0. Отсюда аналогично — расчетная формула метода Ньютона. Метод Ньютона имеет простой геометрический смысл: есть абсцисса точки пересечения касательной к графику функции, построенной в точке, с осью абсцисс. Теорема о сходимости: Если отличны от нуля и сохраняют определенные знаки при, то, причем скорость сходимости определяется неравенством. Здесь m1=min|f'(x)|, xÎ[a,b], M2= max|f''(x)|, xÎ[a,b]. Если f(x0)f''(x0)<0, то можно не прийти к x=x*, если x0 не очень хорошее. Заметим, что если f'(x*)=0, то квадратичной сходимости может и не быть. Например, пусть f(x)=x2. x*=0 — корень второй кратности, расчетная формула xk+1=xk/2 и сходимость линейная. Иногда целесообразно применять модифицированный метод Ньютона.— расчетная формула модифицированного метода Ньютона. Скорость сходимости модифицированного метода значительно меньше. При решении задачи итерационными методами следует обращать внимание на следующие моменты: Расчетная формула. Условие сходимости. Скорость сходимости. Получение решения с заданной точностью e: В методе Ньютона если |xk+1-xk|<e, то |xk-x*|<e. Def fnf(x)=x^3+x – 1 Def fnf(x)=3*x^2+1 Input x, eps 1 y=x- fnf(x)/ fnf(x) print y, fnf(y) If abs(y-x)<eps then 2 x-y:0 to 1 2 print y, fnf(y) End
29.Метод простых итераций (называемый иначе методом последовательных приближений). Аналогично одномерному случаю заменим нелинейную систему эквивалентной специального вида Метод состоит в замене исходного уравнения 1 способ:
C=y(c), f(0)=0, c Для оценки точности можно использовать следующее неравенство: Если y’(x)>0, то Если Метод простых итераций аналогичен методу Ньютона, точнее сказать метод Ньютона является частным случаем метода простых итераций. Программа аналогична. Def fnf(x)=x^3+x – 1 Def fnf(x)=3*x^2+1 Input x, eps 1 y=x- fnf(x)/ fnf(x) print y, fnf(y) If abs(y-x)<eps then 2 x-y:0 to 1 2 print y, fnf(y) End
|
||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 315; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.69.25 (0.006 с.) |


 эквивалентным уравнением
эквивалентным уравнением  и в построении последовательности, сходящейся к точному решению уравнения Xk+1 =
и в построении последовательности, сходящейся к точному решению уравнения Xk+1 = 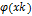 . Такую замену можно сделать разными способами.
. Такую замену можно сделать разными способами.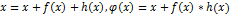 . Сформулируем достаточное условие сходимости метода: пусть функция
. Сформулируем достаточное условие сходимости метода: пусть функция  определена и дифференцируема на интервале [a,b], причем все его значения принадлежат этому интервалу. Тогда существует такое число q, то выполняется условие:
определена и дифференцируема на интервале [a,b], причем все его значения принадлежат этому интервалу. Тогда существует такое число q, то выполняется условие:  на интервале [a,b], то последовательность Xk+1 =
на интервале [a,b], то последовательность Xk+1 =  при любом начальном приближении Хо из интервала[a,b].
при любом начальном приближении Хо из интервала[a,b].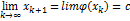
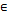 [a,b]
[a,b]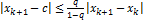
 <0, то
<0, то 



